CH5105 Cookies饼干(线性DP)

题意理解

圣诞老人共有\(M\)个饼干，准备全部分给\(N\)个孩子。

每个孩子有一个贪婪度，第 i 个孩子的贪婪度为 \(g[i]\)。

如果有 \(a[i]\) 个孩子拿到的饼干数比第 \(i\) 个孩子多，那么第 \(i\) 个孩子会产生 \(g[i] \times a[i]\)的怨气。

给定\(N、M\)和序列\(g\)，圣诞老人请你帮他安排一种分配方式，使得每个孩子至少分到一块饼干，并且所有孩子的怨气总和最小。

输入格式

第一行包含两个整数N,M。

第二行包含N个整数表示\(g_1\)~\(g_N\)。

输出格式

第一行一个整数表示最小怨气总和。

第二行N个空格隔开的整数表示每个孩子分到的饼干数，若有多种方案，输出任意一种均可。

数据范围

\[1 \le N \le 30, \\\\
N \le M \le 5000, \\\\
1 \le g_i \le 10^7 \\\\
\]

输入样例：

3 20
1 2 3

输出样例：

2
2 9 9

解题报告

题意理解

\(M\)个饼干,分给\(N\)个孩子,每一个孩子有一个贪婪度\(g[i]\),和嫉妒值\(a[i]\),如果有\(a[i]\)个孩子的饼干数比\(i\)多,那么就会产生怨气\(g[i] \times a[i]\)

要求怨气最少.

思路解析

状态初步

已经获得饼干的孩子个数,和已经发放的饼干,应该是我们的动态规划阶段.

但是我们发现,一个孩子产生的怨气,必然和其他孩子得到的饼干数有关.

\[s[i]=
\begin{cases}
\mathcal a[i] \times g[i] \quad a[i]>0\\\\
\mathcal 0 \quad a[i]=0 \\\\
\end{cases}
\\\\
s[i]表示为第i个孩子他产生的怨气
\]

---

贪心优化

我们发现动态规划的状态设计,想出来不是很难.

但即使我们发现知道了这个状态设计,我们却无法推出动态规划转移方程.

孩子们的怨气产生是根据情况变化的,我们永远猜测不出来.妹子的心就是这样的

我们不得不想点办法?

其实我们发现,那些贪婪度度大的孩子,应该获得到更多的饼干.

所以说,我们按照贪婪度从小到大排序,然后每个孩子获得的饼干数应该也按照贪婪度从大到小排序.

越贪婪的人,得到的饼干越多.越漂亮的妹子,追求者越多

所以说饼干个数,是单调递减的.

---

转移方程

我们可以设置一下状态的具体表示.

\[f[i][j]表示为前i个孩子,一共分配了j个饼干的最小怨气和.
\]

那么状态转移一下.

\[a[i+1]=
\begin{cases}
\mathcal a[i+1]=i \quad cnt[i+1]<cnt[i] \quad 前i个孩子饼干都比他多,饼干数是单调递减的\\\\
\mathcal a[i+1] \quad cnt[i+1]=cnt[i] \quad 难以确定,不知道前面有多少个孩子饼干比他多\\\\
\end{cases}
\\\\
cnt[i]表示第i个孩子得到的饼干数
\]

当前问题就是,让我们去处理未知情况,也就是前面到底有多少个孩子饼干比它多.

---

等价变换

1. 假如说我们当前第\(i\)个孩子,手中的饼干数大于\(1\)的话.

根据饼干数是单调递减可以得出,

\[我们前i个孩子手中的饼干都是 \ge 1 \\\\
因为第i个孩子得到的饼干个数是最少的 \\\\
一个数列中最小值大于1,那么必然其他值都会大于1. \\\\
\]

分配\(j\)个饼干给前\(i\)个孩子,其实等价于分给\(j-i\)个饼干给前\(i\)个孩子.

相当于每一个孩子都少拿一个.

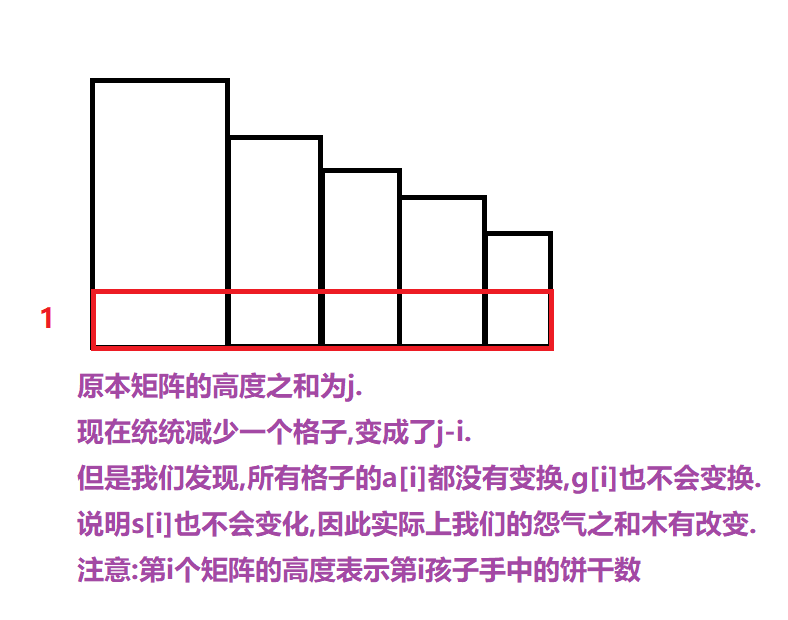
之所以\(a[i]\)没有改变,是因为所有的孩子们,比他们饼干数量多的孩子个数没有改变,相对的逻辑关系木有变化.

1. 假如说第i个孩子只有1个饼干

我们只能选择枚举有多少个孩子只有一个饼干了,肯定不会很多.

\[f[i][j]=min
\begin{cases}
\mathcal f[i][j-i] \\\\
\mathcal min_{0 \le k < i}{F[k,j-(i-k)]+k*\sum_{p=k+1}^{i}{g[p]}} \\\\
\end{cases}
\\\\
\]

---

代码解析

#include <bits/stdc++.h>
using namespace std;
#define fir(i,a,b) for(int i=a;i<=b;i++)
#define int long long
const int N=110;
const int M=5100;
int n,m,i,j,k,f[N][M],s[N],g[N],a[N][M],b[N][M],ans[M],c[N];
int cmp(int a,int b)
{
    return g[a]>g[b];
}
void print(int n, int m)
{
	if (n==0)
	    return;
	print(a[n][m],b[n][m]);
	if (a[n][m] == n)
	{
		fir(i,1,n)
		    ans[c[i]]++;
	}
	else
		fir(i,a[n][m]+1,n)
		    ans[c[i]] = 1;
}
signed main()
{
    ios::sync_with_stdio(false);
    cin>>n>>m;
    fir(i,1,n)
        cin>>g[i],c[i]=i;
    sort(c+1,c+1+n,cmp);
    memset(f,0x3f,sizeof(f));
    f[0][0]=0;
    fir(i,1,n)
	{
		s[i]=s[i-1]+g[c[i]];
		fir(j,i,m)
		{
			f[i][j]=f[i][j-i];
			a[i][j]=i;
			b[i][j]=j-i;
			fir(k,0,i-1)
			{
				if (f[i][j]>f[k][j-(i-k)]+(s[i]-s[k+1-1])*k)
				{
					f[i][j]=f[k][j-(i-k)]+(s[i]-s[k+1-1])*k;
					a[i][j]=k;
					b[i][j]=j-(i-k);
				}
			}
		}
	}
	cout<<f[n][m]<<endl;
    print(n,m);
	fir(i,1,n)
	    cout<<ans[i]<<' ';
	cout<<endl;
    return 0;
}