leetcode-62. Unique Paths · DP + vector

题面

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

Note: m and n will be at most 100.

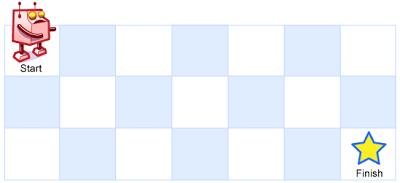
说白了就是：统计从二维数组左上角到右下角总共有多少不同路径。（0 <= m, n <= 100）

样例

Example 1:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right

Example 2:

Input: m = 7, n = 3
Output: 28

思路

由于只能朝下或者右走，稍加推导，我们就可以看出：当前点的路径数就等于它左边点路径数加上上边点路径数，很容易想到递归（很不幸，层数过大，栈会溢出！）。so, 我们只能通过DP循环来做。

算法 : DP

时间复杂度：O(m*n)

空间复杂度：O(m*n)

1. 用二维数组还是一维数组记录状态都可以，我们先用二维来说明问题。即：创建二维数组dp[m][n]

2. 预处理第一行和第一列，因为第一行只能往右走，第一列只能往下走（只有一条路径，所以都初始化为1）

3. 遍历二维DP数组：当前点路径=上边点路径+左边点路径

状态方程：

dp[0][j] = 1

dp[i][0] = 1

dp[i][j] = dp[i-1][j] + dp[i][j-1]

源码

 int uniquePaths(int m, int n) {
         if(m ==  || n == )
             return ;
         int dp[n][m] = {};
         dp[][] = ;
         for(int i=; i<m; i++)
             dp[][i] = ;
         for(int i=; i<n; i++)
             dp[i][] = ;
         for(int i=; i<n; i++)
         {
             for(int j=; j<m; j++)
             {
                 dp[i][j] = dp[i][j-] + dp[i-][j];
             }
         }
         return dp[n-][m-];
 }

优化：空间优化

上面算法，我们使用了二维数组记录DP状态，其实用一维就够了。推到一个简单的例子你就会发现，焦点总是在一行上，只要用一行从上到下滑动，就可达到目的。

时间复杂度：O(m*n)

空间复杂度：O(n)

源码

     int uniquePaths(int m, int n) {
         //空间压缩
          if(m ==  || n == )
             return ;
         int dp[m] = {};
         for(int i=; i<m; i++)
             dp[i] = ;
         for(int i=; i<n; i++)
         {
             dp[] = ;
             for(int j=; j<m; j++)
             {
                 dp[j] = dp[j-] + dp[j];
             }
         }
         return dp[m-];
 　　}