Machine Learning(Andrew Ng)学习笔记

1.监督学习(supervised learning)&非监督学习(unsupervised learning)

监督学习：处理具有若干属性且返回值不同的对象。分为回归型和分类型：回归型的返回值是连续的，分类型的返回值是离散的。

非监督学习：将具有若干属性的相同对象分为不同的群体。

2.线性回归模型(监督学习)

2.1 一些符号

m——训练样本数目

x——输入变量

y——输出变量

(x,y)——一个训练样本

(x⁽ⁱ⁾,y⁽ⁱ⁾)——第i个训练样本

h——假设(hypothesis)——预测函数

n——训练样本特征数目

$x_{i}$——训练样本的第i个特征对应的向量

$x^{(i)}$——第i个训练样本所有特征对应的向量

$x_{j}^{(i)}$——第i个训练样本的第j个特征

2.2 cost function

$J\left ( \theta _{0},\theta _{1} \right )= \frac{1}{2m}\sum_{i=1}^{m}\left ( h_{\theta }\left ( x^{(i)} \right )-y^{(i)} \right )^{2}$

$h_{\theta }(x)=\theta _{0}+\theta _{1}x$

2.3 梯度下降算法(gradient descent)

2.3.1 单特征：

$\theta _{i}:=\theta _{i}-\alpha \frac{\partial }{\partial \theta _{i}}J\left ( \theta _{0}, \theta _{1}\right  ) (simultaneously\ for\ i=0\ and\ i=1)$

$J\left ( \theta _{0},\theta _{1} \right )= \frac{1}{2m}\sum_{i=1}^{m}\left ( h_{\theta }\left ( x^{(i)} \right )-y^{(i)} \right )^{2}$

$h_{\theta }(x)=\theta _{0}+\theta _{1}x$

即

$\theta _{0}:=\theta _{0}-\alpha \frac{1}{m}\sum_{i=1}^{m}\left (h_{\theta }(x^{(i)})-y^{(i)} \right )$

$\theta _{1}:=\theta _{1}-\alpha \frac{1}{m}\sum_{i=1}^{m}\left (h_{\theta }(x^{(i)})-y^{(i)} \right )\cdot x^{(i)}$

2.3.2 多特征：

$\theta _{i}:=\theta _{i}-\alpha \frac{\partial }{\partial \theta _{i}}J\left ( \theta\right  ) (simultaneously\ for\ i=0\ to\ n)$

$\theta = \begin{pmatrix}\theta _{0}
\\\theta _{1}
\\\theta _{2}
\\...
\\\theta _{n}
\end{pmatrix}$

$x^{(i)} = \begin{pmatrix}x_{0}^{(i)}
\\x_{1}^{(i)}
\\x_{2}^{(i)}
\\...
\\x_{n}^{(i)}
\end{pmatrix}(x_{0}^{(i)}=1)$

$J\left (\theta \right )= \frac{1}{2m}\sum_{i=1}^{m}\left ( h_{\theta }(x^{(i)})-y^{(i)} \right )^{2}$

$h_{\theta }(x^{(i)})=\theta ^{T}x^{(i)}$

即

$\theta_{j}:=\theta_{j}-\alpha \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})\cdot x_{j}^{(i)}$

2.3.3

批处理梯度下降("Batch" Gradient Descent)：梯度下降的每一步都要用到所有训练样本的数据

2.4 优化方法

2.4.1 特征缩放(feature scaling)

$x_{j}^{(i)}:=\frac{x_{j}^{(i)}-\mu_{j}}{S_{j}}$

$\mu_{j}$为训练样本的第j个特征的平均值

$S_{j}$为训练样本的第j个特征的标准差(max-min)

2.4.2

(1)工作正确性检验

随着迭代次数(iteration)的增加，代价函数$J(\theta)$不可能增加

当$J(\theta)$减少量小于$\varepsilon $时，认为代价函数已收敛

(2)学习速率($\alpha$)选取

$\alpha$过小：收敛过慢

$\alpha$过大：无法保证每次迭代$J(\theta)$都不增加；无法保证收敛(solution：减小$\alpha$)

3 多项式回归

3.1

直接把f(x)作为一个整体当成$x^{(i)}_{j}$，即可把非线性回归转化为线性回归

3.2 数学方法直接求出最优解

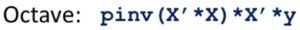
3.3