Logistic Regression(逻辑回归)

分类是机器学习的一个基本问题, 基本原则就是将某个待分类的事情根据其不同特征划分为两类.

• Email: 垃圾邮件/正常邮件
• 肿瘤: 良性/恶性
• 蔬菜: 有机/普通

　　对于分类问题, 其结果 y∈{0,1}, 即只有正类或负类. 对于预测蔬菜是否为有机这件事, y = 0表示蔬菜为普通, y= 1表示蔬菜为有机.

---

　　逻辑回归是分类问题中的一个基本算法, 它的猜想函数h_θ(x) = g(θ^T*x)

　　其中, g(z) = 1 / (1+e^-z), 该函数称为sigmoid函数或logistic函数, 是一个增函数,输出映射g(z)∈[0,1].

　　h_θ(x)表示当输入为x, (权重)参数为θ时, 预测y=1的概率.

---

代码实现:

function g = sigmoid(z)
%SIGMOID Compute sigmoid function
% g = SIGMOID(z) computes the sigmoid of z.

g = zeros(size(z));

for i = 1:size(z,1)
　　for j = 1:size(z,2)
　　　　g(i,j) = 1/(1+e^(-z(i,j)));
　　endfor
endfor

end

---

　　对于逻辑回归的猜想函数h_θ(x) = g(θ^T*x), 当θ^T*x = 0时, h_θ(x) = 0.5. 而我们规定当h_θ(x) >= 0.5, 即θ^T*x >=0时, 预测结果 y =1, 当h_θ(x) <0.5时,预测结果 y= 0.

　　因此, 通过给定的权重参数矩阵与特征值, 可以计算出该预测函数的决策边界 , 通过这条边界即可将问题进行分类.

---

　　逻辑回归算法的代价函数表示当预测值与实际值产生偏差时所承受的惩罚大小, 公示表示为cost(h_θ(x), y) = -log(h_θ(x)), if y =1, -log(1-h_θ(x)), if y = 0.

　　当y=1时，假定这个样本为正类。如果此时h_θ(x) = 1,则对这个样本而言的cost=0,表示这个样本的预测完全准确。但是如果此时预测的概率h_θ(x) = 0，那么cost→∞。直观解释的话，由于此时样本为一个正样本，但是预测的结果P(y=1|x;θ) = 0, 也就是说预测 y=1的概率为0，那么此时就要对损失函数加一个很大的惩罚项。当y = 0时, 道理相同.

---

　　为了获得更准确的分类决策边界, 我们需要调节代价函数到最小值, 这时, 预测值与实际结果间偏差最小. 为了最小化代价函数, 我们需要调节参数θ. 比较常用的方法为梯度下降法.

　　梯度下降是迭代法的一种, 其计算过程就是沿梯度下降的方向求解极小值.　

　　逻辑回归代价函数J(θ):

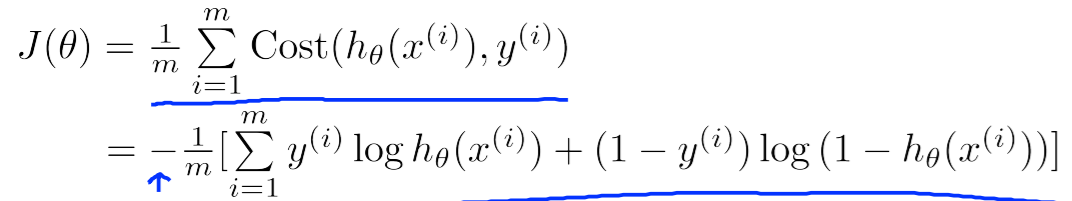
　　为了最小化J(θ), 需要不断重复减小θ的值直到J(θ)收敛:

　　其中α为学习速率, 即每次下降的步长大小, 如果α过于大, 可能导致无法收敛, 如果α过于小, 可能导致收敛速度过慢.

---

代码实现:

function [J, grad] = costFunction(theta, X, y)
%COSTFUNCTION Compute cost and gradient for logistic regression
% J = COSTFUNCTION(theta, X, y) computes the cost of using theta as the
% parameter for logistic regression and the gradient of the cost
% w.r.t. to the parameters.

% Initialize some useful values
m = length(y); % number of training examples

J = 0;
grad = zeros(size(theta));

Jtmp=0;
h= zeros(m,1);

%step1:compute hx
hx = X * theta;

%step2:compute h(hx)
h = sigmoid(hx);

%step3:compute cost function's sum part
for i=1:m,
　　Jtmp=Jtmp+(-y(i)*log(h(i))-(1-y(i))*log(1-h(i)));
endfor
J=(1/m)*Jtmp;

%step4:compute gradient's sum part 
sum1 =zeros(size(X,2),1);%#features row
for i=1:m
　　sum1 = sum1+(h(i)-y(i)).*X(i,:)';
endfor

grad= (1/m)*sum1;

end