SVM-笔记(1)
1 目的
SVM推导是从讨论最优超平面开始的,即为了得到一个能够划分不同超平面的面,即公式1:
\begin{equation}w^Tx+b=0 \tag{1} \end{equation}
这个公式怎么来的,其实就是基于2维推导过来的,当二维图像时,也就是熟悉的x,y坐标系。我们将一条线的函数公式定义为\(Ax+By+C=0\),其法向量为(A,B),而平面上任意一点(x0,y0)到该线的距离为[参考]:式子2\[d = \frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}} \tag{2}\]
类比得到,多维平面上的某个“线”,其公式为\(Ax+By+Cz+D=0\),可以看出就是一个向量\(w = [A,B,C]\)与另一个向量\(X = [x,y,z]\)之间的内积加上一个常量D。也就是上述式子1。所以,SVM中某点到该“线”的距离公式从式子2类比得到为,式子3:\[r = \frac{|w^Tx+b|}{||w||} \tag{3}\]
其法向量为\(w\)。
ps:下面参考自周志华老师的《机器学习》,支持向量机部分。
2 最优超平面
为了方便,则将此超平面记为\((w,b)\)。我们取二分类样本,即样本标签为\(\{+1,-1\}\)。我们希望超平面能够正确分类,也就是对于\(y_i = +1\)的样本,\(w^Tx_i+b>0\);而对于\(y_i = -1\)的样本,\(w^Tx_i+b<0\)。
ps:这里需要接着解释下为什么间隔取1,此部分资料在Andrew Ng的网易公开课讲义部分有说道,后续有空我过来补齐。
而为了获得最优的超平面,我们假设离该平面最近的点到该平面距离至少为1.则满足下面式子4:
\[\begin{cases}
w^Tx_i+b \geq +1, y_i = +1\\
w^Tx_i+b \leq -1, y_i = -1
\end{cases} \tag{4}\]
所以两个不同类别之间最小的距离为,式子5:
\[r = \frac{2}{||w||} \tag{5}\]
所以式子5,也被称为"间隔"(margin)。
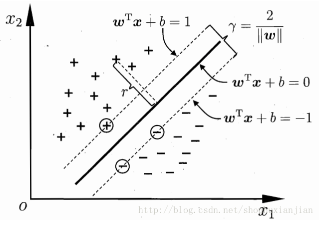
如果将该间隔最大化,那么也就是找到了最优超平面,因为该超平面就是中间那条线,而图上虚线上的正负点,就是所谓的支持向量。即只有这些点才对最优超平面的选取有关。
所以,问题就转换成了求取下面方程式的问题,式子6:
\[\begin{cases}
max_{w,b} \quad \frac{2}{||w||}\\ s.t.\quad y_i(w^Tx_i+b) \geq 1, \quad i=1,2,...,m
\end{cases} \tag{6}\]
可以看到所谓最大化一个分数,其分子不变,也就是最小化一个分母即可,即式子6等同于式子7:
\[\begin{cases}
min_{w,b} \quad \frac{1}{2}||w||^2\\ s.t. \quad y_i(w^Tx_i+b) \geq 1, \quad i = 1,2,...,m
\end{cases} \tag{7}\]
3 拉格朗日浅析
式子7,是一个凸二次规划问题,也就是其一定会有最值存在,为了更快的进行求解,需要用到拉格朗日乘子方法。其实拉格朗日乘子法,在《同济版高数书 第9章多元函数微分法及其应用 第8节多元函数的极值及其求法》上有简单介绍,不过其并没说到KKT等情况,这里还是以网上别人博客作为参考[2,3]:
- 拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush-Kuhn-Tucker)条件是求解约束优化问题的重要方法,在有等式约束时使用拉格朗日乘子法,在有不等约束时使用KKT条件。前提是:只有当目标函数为凸函数时,使用这两种方法才保证求得的是最优解[2]
如博文[3]所说,一般最优化问题,通常为3种,:
(1)无约束优化问题,:
\[min \quad f(x) \tag{8}\]
(2) 等式约束优化问题,假设有n个等式约束:
\[\begin{cases}
min \quad f(x)\\ s.t. \quad h_i(x) = 0;i =1,...,n
\end{cases} \tag{9}\]
(3)不等式约束优化问题,假设有n个等式约束,m个不等式约束:
\[\begin{cases}
min \quad f(x),\\ s.t. \quad h_i(x) = 0; i=1,...,n\\ \qquad\quad g_i(x) \leq 0; j = 1,...,m
\end{cases} \tag{10}\]
- 对于第(1)类的优化问题,常常使用的方法就是Fermat定理,即使用求取\(f(x)\)的导数,然后令其为零,可以求得候选最优值,再在这些候选值中验证;如果是凸函数,可以保证是最优解[3] 。
即直接求其导数,然后求得导数为0的解即可。
- 对于第(2)类的优化问题,常常使用的方法就是拉格朗日乘子法(Lagrange Multiplier) ,即把等式约束h_i(x)用一个系数与f(x)写为一个式子,称为拉格朗日函数,而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导,令其为零,可以求得候选值集合,然后验证求得最优值 [3]。
即先将函数\(f(x)\)与其约束函数\(h_i(x)\)变换成一个单一函数,即:
\[L(x,\lambda) = f(x)+\lambda h(x)\]详细点说,就是:\[L(x,\lambda) = f(x)+\sum_{i=0}^n \lambda_ih_i(x)\] 然后基于这个函数对变量\(x\),\(\lambda\)求导,并将取值为0的解带入原问题中,比较哪个值最小,从而得到最优解。
- 对于第(3)类的优化问题,常常使用的方法就是KKT条件。同样地,我们把所有的等式、不等式约束与f(x)写为一个式子,也叫拉格朗日函数,系数也称拉格朗日乘子,通过一些条件,可以求出最优值的必要条件,这个条件称为KKT条件 [3]。
如上一样,只是函数变成了:\[L(x,a,b) =f(x)+ \sum_{i=0}^na_ih_i(x)+\sum_{i=0}^mb_ig_i(x) \tag{11}\]
然后针对每个变量参数求导,通过联合所有的求导式子,将其等于0,求得极值点,再将极值点带入,求得最值点即可。而KKT中有个要求即\(b_ig_i(x)=0\),但因为\(g_i(x) \leq 0\),所以要么\(b_i = 0\),要么\(g_i(x)=0\)。而这也和SVM中的支持向量有很密切的关系。
4 对偶问题
可以看出式子7可以通过KKT求解,添加拉格朗日乘子\(\alpha_i \geq 0\)写成拉格朗日函数为,式子12:
\[L(w,b,\alpha)=\frac{1}{2}||w||^2+\sum_{i=1}^m \alpha_i(1-y_i(w^Tx_i+b)) \tag{12}\]
其中\(\alpha_i \geq 0\),这样就保证了后面一项一定小于0。其中\[\alpha = (\alpha_1;\alpha_2;...;\alpha_m) \tag{13}\]将\(L(w,b,\alpha)\)对\(w\),\(b\)进行求偏导得,式子14,式子15:
\[\begin{cases}
w=\sum_{i=1}^m \alpha_i y_i x_i \tag{14,15}\\
0 = \sum_{i=1}^{m}\alpha_i y_i
\end{cases}\]
将上述式子14带入\(L(w,b,\alpha)\),将\(w\),\(b\)消去,再考虑式子15,得如下对偶问题, 式16:
\[\begin{cases}
max_\alpha \quad \sum_{i=1}^m\alpha_i - \frac{1}{2} \sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_j y_i y_j x_i^T x_j \\
s.t. \qquad \sum_{i=1}^m \alpha_i y_i =0, \\
\qquad \qquad \alpha_i \geq 0, i=1,2,...,m
\end{cases} \tag{16}\]
在求得\(\alpha\)向量时,则通过式子14,即可得到\(w\),从而带入原式子,得到,式17:
\[\begin{eqnarray}f(x,y)
&=&w^Tx+b\\
&=&\sum_{i=1}^m \alpha_i y_i x_i^Tx+b
\end{eqnarray} \]
这里的拉格朗日乘子就是\(\alpha\),其中每一个变量\(\alpha_i\)都对应着一个样本\((x_i,y_i)\),且式子7中还有不等式存在,按照之前KKT部分说的,要求\((L(x,a,b))\)不等式部分等于0,即\(\alpha_i(y_if(x_i) - 1) = 0\),则要求联合一起,得到如下约束:
\[\begin{cases}
\alpha_i \geq 0; \\
y_if(x_i) -1 \geq 0;\\
\alpha_i(y_if(x_i) - 1) = 0
\end{cases} \tag{18}\]
所以对于任意训练样本\((x_i,y_i)\)总有\(\alpha_i = 0\)或者\(y_if(x_i)=1\).如果当前\(a_i=0\),那么该式在式17中则会不存在,而如果有\(\alpha_i \geq 0\)那么一定会有\(y_if(x_i)=1\),即对应的这个样本刚好位于最大间隔边界上,是一个支持向量。即SVM的一个性质:当训练完成后,大部分训练样本无需保留,只要保留支持向量即可,而且模型也只与支持向量有关。
因为这是一个二次规划问题,而且模型的训练速度正比于训练样本数,所以不适合超大数据集,而且中间会有一堆的开销,为了解决这种问题,通过问题本身的特性,有如SMO等高效方法来进行求解。(待更新)
5 - 核函数
对于线性不可分的样本集合来说,在低维空间中,是无法将其区分的。而且如果原始样本的特征维度是有限维,那么一定存在某个高维,能够将其线性区分,所以,升维,升到线性可分的维度,就能解决这个问题。
假设\(\phi(x)\)是\(x\)升维后的特征向量,则在能够划分超平面的特征空间中模型表示为:
\[f(x) = w^T\phi(x)+b \tag{5.1}\]
表示成式子7如:
\[\begin{cases}
min_{w,b} \quad \frac{1}{2}||w||^2 \\ s.t. \qquad y_i(w^T\phi(x_i)+b) \geq1, i = 1,2,...,m
\end{cases} \tag{5.2}\]
其对偶问题:
\[\begin{cases}
max_\alpha\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\phi(x_i)^T\alpha(x_j) \\s.t. \qquad \sum_{i=1}^m\alpha_iy_i=0,\\\qquad\quad\alpha_i \geq 0,i = 1,2,..,m
\end{cases} \tag{5.3}\]
这样就将问题转换到了求高维特征的内积问题,可是如果这时候的特征空间维度太高,那么内积的计算都是很困难的。所以如果能够有这样一类函数:
\[\kappa(x_i,x_j) = \quad<\phi(x_i),\phi(x_j)>\quad= \phi(x_i)^T\phi(x_j) \tag{5.4}\]
即希望找到一个函数,使得\(x_i\)与\(x_j\)在特征空间的内积就等于他们在原始样本空间通过升维得到的内积。这样就免去了计算高维甚至无穷维度的问题,式子5.3重写成:
\[\begin{cases}
max_\alpha\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\kappa(x_i,x_j) \\s.t. \qquad \sum_{i=1}^m\alpha_iy_i=0,\\\qquad\quad\alpha_i \geq 0,i = 1,2,..,m
\end{cases} \tag{5.5}\]
求解后:
\[\begin{eqnarray}f(x,y)
&=&w^Tx+b\\
&=&\sum_{i=1}^m \alpha_i y_i \phi(x_i)^T\phi(x)+b\\
&=&\sum_{i=1}^m \alpha_i y_i \kappa(x_i,x)+b
\end{eqnarray} \]
(待续)
6 - 软间隔,惩罚系数
如前面说的,一直假定训练样本在样本空间或者特征空间中能够达到线性可分,可是现实问题总是更复杂的,也很难说找到合适的核函数来让训练样本在特征空间中线性可分,即使找到了,也难保这个线性可分的结果不是过拟合造成的。所以,由此那么就放宽条件,允许一部分样本是分类错误的,比如:
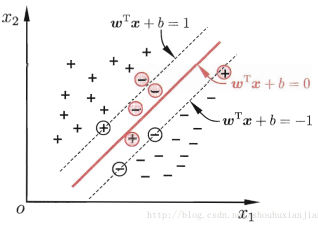
,所谓的"硬间隔",就是每个样本都完全满足SVM的目标函数定义,而“软间隔”,就是允许及个别的样本不满足:
\[y_i(w^Tx_i+b) \geq 1 \tag{6.1}\]
为了尽可能的减少这种情况存在,所以需要惩罚这种样本,从而目标函数改成了:
\[min_{w,b}\frac{1}{2}||w||^2+C\sum_{i=1}^m l_{0/1}(y_i(w^Tx_i+b)-1) \tag{6.2}\]
其中\(C>0\) 是一个常量,即惩罚系数,\(l_{0/1}\)是"0/1损失函数":
\[l_{0/1}(z) = \begin{cases}1,\quad if \quad z < 0;\\ 0,\quad otherwise\end{cases} \tag{6.3}\]
可以发现当\(C\)无穷大时,满足最严格要求,即所有样本都必须分类正确,而当\(C\)有确定值时,就是一定程度的让步。
可是因为损失函数通常是非凸,非连续,数学性质不够完美,所以式子6.2很难求。所以通常是采用一些凸的连续的,且是损失函数上界的一些函数来代替。
2017/03/08 第一次修改!
- [1] 周志华 《机器学习》
- [2] 拉格朗日乘子法和KKT条件
- [3] 深入理解拉格朗日乘子法和KKT条件
- [4] 再生核希尔伯特空间
SVM-笔记(1)的更多相关文章
- SVM 笔记整理
支持向量机 一.支持向量机综述 1.研究思路,从最特殊.最简单的情况开始研究 基本的线性的可分 SVM 解决二分类问题,是参数化的模型.定义类标记为 \(+1\) 和 \(-1\)(区别于感知机,感知 ...
- SVM笔记
1.前言 SVM(Support Vector Machine)是一种寻求最大分类间隔的机器学习方法,广泛应用于各个领域,许多人把SVM当做首选方法,它也被称之为最优分类器,这是为什么呢?这篇文章将系 ...
- 机器学习支持向量机SVM笔记
SVM简述: SVM是一个线性二类分类器,当然通过选取特定的核函数也可也建立一个非线性支持向量机.SVM也可以做一些回归任务,但是它预测的时效性不是太长,他通过训练只能预测比较近的数据变化,至于再往后 ...
- Jordan Lecture Note-8: The Sequential Minimal Optimization Algorithm (SMO).
The Sequential Minimal Optimization Algorithm (SMO) 本文主要介绍用于解决SVM对偶模型的算法,它于1998年由John Platt在论文“Seque ...
- 机器学习实战笔记(Python实现)-05-支持向量机(SVM)
--------------------------------------------------------------------------------------- 本系列文章为<机器 ...
- SVM基本思想和对偶推导笔记-记录毕业论文1
快毕业啦~~记得上一篇论文利用JointBoost+CRF做手绘草图的分割项目在3月份完结后,6月份去实习,9月份也没怎么认真找工作就立刻回来赶论文(由于分割项目与人合作难以写入毕业论文),从9月到1 ...
- 机器学习技法--学习笔记04--Soft SVM
背景 之前所讨论的SVM都是非常严格的hard版本,必须要求每个点都被正确的区分开.但是,实际情况时很少出现这种情况的,因为噪声数据时无法避免的.所以,需要在hard SVM上添加容错机制,使得可以容 ...
- 机器学习实战 - 读书笔记(06) – SVM支持向量机
前言 最近在看Peter Harrington写的"机器学习实战",这是我的学习笔记,这次是第6章:SVM 支持向量机. 支持向量机不是很好被理解,主要是因为里面涉及到了许多数学知 ...
- opencv学习笔记(七)SVM+HOG
opencv学习笔记(七)SVM+HOG 一.简介 方向梯度直方图(Histogram of Oriented Gradient,HOG)特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子 ...
- [置顶] 最优间隔分类器、原始/对偶问题、SVM的对偶问题——斯坦福ML公开课笔记7
转载请注明:http://blog.csdn.net/xinzhangyanxiang/article/details/9774135 本篇笔记针对ML公开课的第七个视频,主要内容包括最优间隔分类器( ...
随机推荐
- 唯一索引的一种使用情景【有则U无则I】
这个知识点是最近一位面试老师问我的,当时对这种方法不了解,所以只能说那个中效率低的方法了,也就是先进性select判断,然后在执行更新或者插入操作,显然这种是很麻烦的,也自我反思一下,确实有很多的知识 ...
- 不能用notepad++编辑器编写python
不能用notepad++编辑器编写python,因为notepad对空格支持不是很良好,会出现莫名其妙的错误!建议用vim或emacs. 有人这样解释:不要混合使用制表符和空格来缩进,因为这在跨越不同 ...
- git 入门教程之个性化 git
前情概要 初识 git 时,我们就已经接触过 git 的基本配置,使用 git config 命令配置用户名和邮箱: # 配置当前项目(`local`)的用户名(`snowdreams1006`) g ...
- JS辨别访问浏览器判断是android还是ios系统
function isIOSOrAndroid() { var browser = { versions: function() { var u = navigator.userAgent, app ...
- Django 2.0 URL新版配置介绍
实例 先看一个例子: from django.urls import path from . import views urlpatterns = [ path('articles/2003/', v ...
- mssql sqlserver update delete表别名用法简介
转自:http://www.maomao365.com/?p=6973 摘要: 在sql脚本编写中,如果需要在update delete 中使用表别名的方法,必须按照一定的规则编写,否则将会出现相应 ...
- mssql sqlserver 使用sql脚本输出交替不同的背景色的html信息的方法分享
转自:http://www.maomao365.com/?p=6679 摘要: 下文将分享使用sql脚本输出交替变换的不同背景颜色的sql脚本的方法分享,如下所示: 实验环境:sqlserver 20 ...
- 纯JS编写打地鼠游戏
这个游戏是本人前不久刚入门编写的游戏,感觉里面代码很LOW但是对于新手来说很一般般吧~ 没有上传音乐文件了 运行效果: 上代码(HTML+JS): <!DOCTYPE html> < ...
- 平衡二叉树(Balanced Binary Tree 或 Height-Balanced Tree)又称AVL树
平衡二叉树(Balanced Binary Tree 或 Height-Balanced Tree)又称AVL树 (a)和(b)都是排序二叉树,但是查找(b)的93节点就需要查找6次,查找(a)的93 ...
- Unity 琐碎(4) 可视化辅助调试Giamos
Gizmos 类 可以在代码中绘制一些输出结果或者中间输出内容,比如计算后的包围盒等等 类变量 方法 作用 color 控制输出颜色 matrix Set the gizmo matrix used ...
