隐马尔可夫模型HMM(二)概率计算问题
摘自
1.李航的《统计学习方法》
2.http://www.cnblogs.com/pinard/p/6955871.html
一、概率计算问题
上一篇介绍了概率计算问题是给定了λ(A,B,π),计算一个观测序列O出现的概率,即求P(O|λ)。
用三种方法,直接计算法,前向算法,后向算法。
考虑隐马尔可夫模型(一)中的盒子球模型。
假设Q={1,2,3,4}, V = {红,白},在给定λ(A,B,π)的条件下,其中:
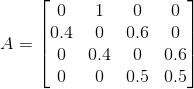 ,
, 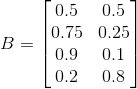 ,
,

求O=(红,白,红)的概率。
二、直接计算法
说通俗一点,就是暴力求解,穷举法。
- 所有可能的状态序列I,则状态序列I的概率为P(I|λ)
- 对于固定的状态序列I,则观测序列为O的概率P(O|I,λ)
- 联合概率为P(O,I|λ) = P(O|I,λ)P(I|λ)
- 则最后所求为P(O|λ) = ΣP(O|I,λ)P(I|λ)
状态集合有N个,一共有T个状态序列,所以状态序列的可能性为NT,每一种状态序列都要相应乘以T个观测概率矩阵,所以最后的时间复杂度为O(TNT)。
三、前向计算法
记αi(j)为部分观测序列为o1.....ot切ot状态为qj的概率。
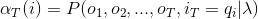
首先,记alphai(j)为第i次观测下状态为j,观测值为O(i)的概率,bj(i)为j状态下观测值为O(i)的概率, 暂时记i=1为红球,i=2为白球, aij为矩阵A中i行j列。
1、第一次观测为红球
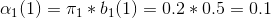


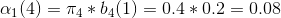
2、第二次观测为白球

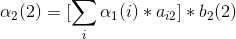
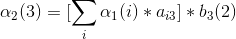
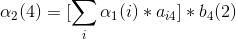
3、第三次观测
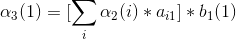
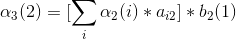
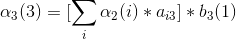
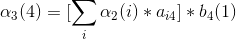
4、最后结果
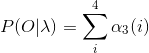
四、后向计算方法
βt(i)为On, On-1.... Ot观测序列且在Ot时刻状态为qi的概率:
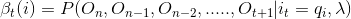
五、总结
根据前向传播算法,可以得到一些相关概率和期望。
1、给定模型输入λ和观测O,在时刻t处于状态qi 的概率为γt(i)。
(1)记γt(i):
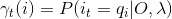
(2)由前向概率和后向概率表达式α和β可得:
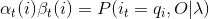
(3)因此:

(4)因此得到γt(i)
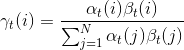
2、给定模型λ和观测O,在时刻t处于状态qi,且在时刻t+1处于状态qj的概率为εt(i, j)。
(1)记εt(i, j):
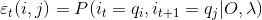
(2)通过前向后向计算可以得到:

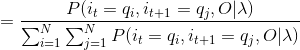
(3)由于:
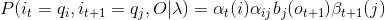
(4)因此:
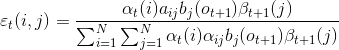
3、在观测O下由状态i出现的期望值:

4、在观测O下由状态i转移的期望值
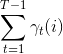
5、在观测O下由状态i转移到状态j的期望值:
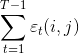
隐马尔可夫模型HMM(二)概率计算问题的更多相关文章
- 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比算法 ...
- 隐马尔可夫模型HMM与维特比Veterbi算法(二)
隐马尔可夫模型HMM与维特比Veterbi算法(二) 主要内容: 前向算法(Forward Algorithm) 穷举搜索( Exhaustive search for solution) 使用递归降 ...
- 隐马尔科夫模型HMM学习最佳范例
谷歌路过这个专门介绍HMM及其相关算法的主页:http://rrurl.cn/vAgKhh 里面图文并茂动感十足,写得通俗易懂,可以说是介绍HMM很好的范例了.一个名为52nlp的博主(google ...
- 猪猪的机器学习笔记(十七)隐马尔科夫模型HMM
隐马尔科夫模型HMM 作者:樱花猪 摘要: 本文为七月算法(julyedu.com)12月机器学习第十七次课在线笔记.隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来 ...
- 隐马尔科夫模型HMM(一)HMM模型
隐马尔科夫模型HMM(一)HMM模型基础 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比 ...
- 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比算法 ...
- 隐马尔科夫模型HMM(四)维特比算法解码隐藏状态序列
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数 隐马尔科夫模型HMM(四)维特比算法解码隐藏状态 ...
- 用hmmlearn学习隐马尔科夫模型HMM
在之前的HMM系列中,我们对隐马尔科夫模型HMM的原理以及三个问题的求解方法做了总结.本文我们就从实践的角度用Python的hmmlearn库来学习HMM的使用.关于hmmlearn的更多资料在官方文 ...
- HMM:隐马尔可夫模型HMM
http://blog.csdn.net/pipisorry/article/details/50722178 隐马尔可夫模型 隐马尔可夫模型(Hidden Markov Model,HMM)是统计模 ...
- 机器学习之隐马尔科夫模型HMM(六)
摘要 隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来描述一个含有隐含未知参数的马尔科夫过程.其难点是从可观察的参数中确定该过程的隐含参数,然后利用这些参数来作进一步 ...
随机推荐
- CodeForces - 589B(暴力)
题目链接:http://codeforces.com/problemset/problem/589/B 题目大意:告诉你n 个矩形,知道矩形的长度和宽度(长和宽可以互换),每个矩形的长度可以剪掉一部分 ...
- 搭建简易的WebServer(基于pyhton实现简易Web框架 使用socket套接字)
1. 使用web底层socket的方式实现简易服务器的搭建,用来理解学习 # 1.导入socket模块 import socket import re import gevent import sys ...
- Git同步远程fork的项目
通过fork创建的项目,如果远程仓库代码进行了更新,本地需要同步的话,可以在git上创建一个上游仓库 步骤 运行git remote add upstream https://github.com/O ...
- VS Code汉化
F1搜索 Configure Language { // Defines VS Code's display language. // See https://go.microsoft.com/fw ...
- MVC过滤器处理Session过期
一.自定义一个Action过滤器 public class CheckSession: ActionFilterAttribute { public override void OnActionExe ...
- django2用模板代码图标字体丢失报404 cJZKeOuBrn4kERxqtaUH3T8E0i7KZn-EPnyo3HZu7kw.woff
以前开发网站,不是用php就是用c#或java写后端,跟后端繁重麻烦的代码相比,前端的html+css+JavaScript简直就简单的不算技术,相比之下,工作量也不大. 但如果用django框架,使 ...
- 测试利器 Postman
一.安装 官网:https://www.getpostman.com/ Postman是一个Chrome的一个插件工具,我们可以通过Chrome的应用商店进行进行搜索并安装,安装完成会在桌面上显示一个 ...
- http uri唯一标识
URI:唯一标识并且信息资源(简单理解为:发邮件的地址,身份证号).uri包括url 比如通过查找一个uri,找到一张图片“https://timgsa.baidu.com/timg?image&am ...
- Codeforces Round #518 (Div. 2) B LCM
传送门 https://www.cnblogs.com/violet-acmer/p/10163375.html 题解: 这道题有点意思,有点数学的味道. 根据定义“[a,b] / a”可得这求得是l ...
- c#中数组的总结
Array数组: 基本定义:string[] Scences={"sky","star","sun"} 或者 int[] Scences= ...
