Go斐波拉契数列(Fibonacci)(多种写法)

1 前言

斐波拉契数列有递归写法和尾递归和迭代写法。

2 代码

//recursion
func fib(n int) int{
	if n < 2{
		return n
	}else{
		return fib(n-1) + fib(n-2)
	}
 
}
 
func fibcore(n int) (int,int){
	if n < 2{
		return 0,n
	}else{
		a,b := fibcore(n-1)
		return b,a+b
	}
 
}
 
//tail recursion
func fib2(n int)(int){
	_,b:= fibcore(n)
	return b
}
 
//iteration
func fib3(max int)(int){
	n:=0
	a,b:=0,1
	for {
		if n < max{
			a,b = b,a+b
			n ++
		}else{
			break
		}
	}
	return b
}

3 性能分析

测试第40个的数列值

递归

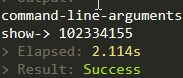
尾递归（参数是40,100都大约是这个时间量）

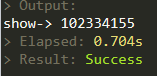
迭代（参数是40,100都大约是这个时间量）

说明：本质上尾递归就是迭代，只是写法略有差别