8皇后问题(c++/python实现)

问题描述：在8*8的国际象棋盘上摆放8个皇后，使其不能互相攻击，即任何两个皇后都不能处于同一行、同一列或者同一斜线上，问有多少种摆法。

算法分析：

　　利用3个数组分表来标记冲突，数组a、b、c。

　　a数组代表列冲突，a[0]~a[7]代表0~7列，如果a[0]=1，则表示第0列已有皇后。

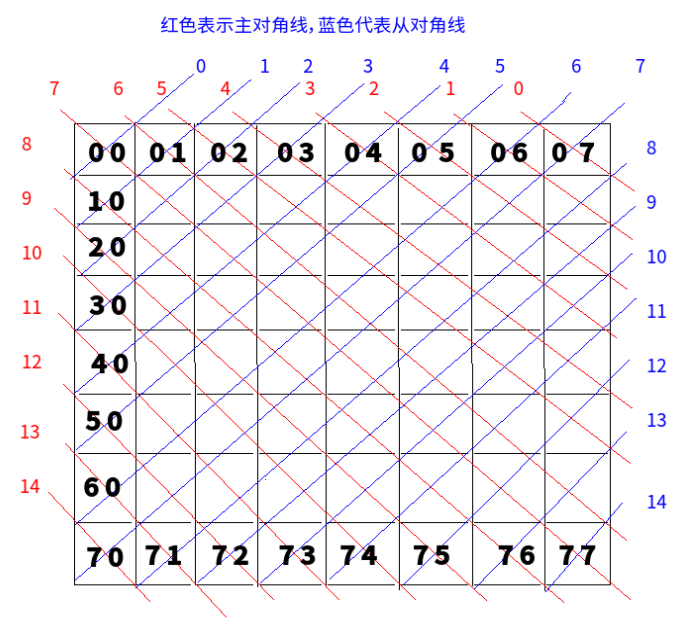
　　b数组带表主对角线冲突，为b[行-列+7]，即b[0]~b[14]中如果为1，表示该主对角线有皇后(如下图)。

　　c数组带表从对角线冲突，为c[行+列]，即c[0]~c[14]中如果为1，表示该从对角线有皇后(如下图)。　　

c++实现如下：

#include <iostream>

using namespace std;

static char Queen[][];
static int a[];
static int b[];
static int c[];
static int iQueenNum=; //记录总的棋盘状态数

void qu(int i);//第i行

int main()
{
    int iLine,iColumn;
    for(iLine=;iLine<;iLine++)//初始化棋盘为‘*’
    {
        a[iLine]=;//列标记初始化，表示无列冲突
        for(iColumn=;iColumn<;iColumn++)
        {
            Queen[iLine][iColumn]='*';
        }
    }
    //主、从对角线标记初始化，表示没有冲突
    for(iLine=;iLine<;iLine++)
    {
        b[iLine]=c[iLine]=;
    }
    qu();
    return ;
}

void qu(int i)
{
    int iColumn;
    for(iColumn=;iColumn<;iColumn++)
    {
        if(a[iColumn]==&&b[i-iColumn+]==&&c[i+iColumn]==)
        {
            Queen[i][iColumn]='@';//放皇后
            a[iColumn]=;//标记，下一次该列上下不能放皇后
            b[i-iColumn+]=;//标记，下一次该主对角线上下不能放皇后
            c[i+iColumn]=;//标记，下一次该从对角线上下不能放皇后
            if(i<)qu(i+);//如果行还没有遍历完，进入下一行
            else//否则输出
            {
                //输出棋盘状态
                int iLine,iColumn;
                cout<<"第"<<++iQueenNum<<"种状态为："<<endl;
                for(iLine=;iLine<;iLine++)
                {
                    for(iColumn=;iColumn<;iColumn++)
                    {
                        cout<<Queen[iLine][iColumn];
                    }
                    cout<<endl;
                }
                cout<<endl;
            }
            //如果前次的皇后放置导致后面的放置无论如何都不能满足要求，则回溯，重置
            Queen[i][iColumn]='*';
            a[iColumn]=;
            b[i-iColumn+]=;
            c[i+iColumn]=;
        }
    }
}

python实现如下：

#-*- coding:utf-8 -*-

global Queue,a,b,c,queenNum
Queue=[['*' for i in range(0,8)] for i in range(0,8)]
a=[0 for i in range(0,8)]
b=[0 for i in range(0,15)]
c=[0 for i in range(0,15)]
queenNum=0
'''
    Queue表示整个棋盘
    a表示列的冲突
    b表示正对角冲突
    c表示从对角冲突
    queenNum表示第几种摆法
'''

def fun(num):
    global Queue, a, b, c, queenNum
    for icolumn in range(0,8):  #总共8行
        if a[icolumn]==0 and b[num-icolumn+7]==0 and c[num+icolumn]==0: #满足3个条件
            Queue[num][icolumn]='@'
            a[icolumn]=1    #该列不能放入皇后
            b[num-icolumn+7]=1  #该正列不能放入皇后
            c[num+icolumn]=1    #该从列不能放入皇后
            if num<7:
                fun(num+1)
            else:   #7行放满了，输出
                queenNum+=1
                print '第%d种情况：'%queenNum
                for j in range(0,8):
                    print ' '.join(Queue[j])
                print '\n'
            #回溯
            Queue[num][icolumn]='*'
            a[icolumn]=0
            b[num-icolumn+7]=0
            c[num+icolumn]=0
if __name__=='__main__':
    fun(0)