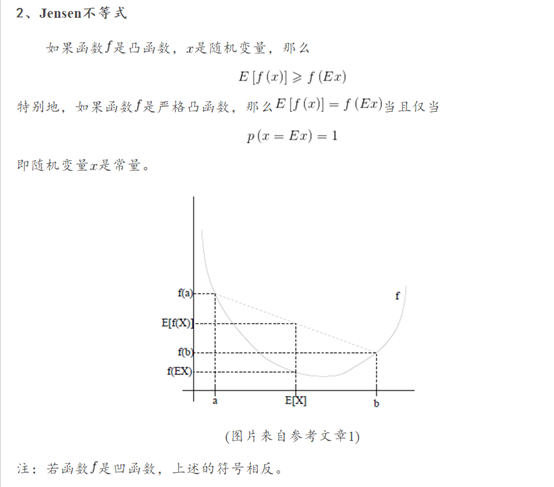
Jensen不等式
Jensen不等式的更多相关文章
- 机器学习数学|微积分梯度jensen不等式
机器学习中的数学 觉得有用的话,欢迎一起讨论相互学习~Follow Me 原创文章,如需转载请保留出处 本博客为七月在线邹博老师机器学习数学课程学习笔记 索引 微积分,梯度和Jensen不等式 Tay ...
- 数学分析中jensen不等式由浅入深进行教学(转)
中国知网:数学分析中Jensen不等式由浅入深进行教学
- Jensen 不等式
若f(x)为区间I上的下凸(上凸)函数,则对于任意xi∈I和满足∑λi=1的λi>0(i=1,2,...,n),成立: \[f(\sum ^{n} _{i=1} \lambda _{i}x_{i ...
- 归并排序、jensen不等式、非线性、深度学习
前言 在此记录一些不太成熟的思考,希望对各位看官有所启发. 从题目可以看出来这篇文章的主题很杂,这篇文章中我主要讨论的是深度学习为什么要"深"这个问题.先给出结论吧:"深 ...
- 【数学基础篇】---详解极限与微分学与Jensen 不等式
一.前述 数学基础知识对机器学习还有深度学习的知识点理解尤为重要,本节主要讲解极限等相关知识. 二.极限 1.例子 当 x 趋于 0 的时候,sin(x) 与 tan(x) 都趋于 0. 但是哪一个趋 ...
- 从Jensen不等式到Minkowski不等式
整理即证 参考资料: [1].琴生不等式及其加权形式的证明.Balbooa.https://blog.csdn.net/balbooa/article/details/79357839.2018.2 ...
- 凸函数与Jensen不等式
这个是在凸优化里面看的,在EM算法中看有用到,所以用latex写了篇回忆用的小短文,现在不会把latex产生的pdf怎么转变成放到这里的内容. 所以我选择直接贴图. 这个pdf可以在我的资源里找到. ...
- MM bound 与 Jensen's inequality
MM bound 与 Jensen's inequality 简森不等式 在使用最大似然估计方法求解模型最优解的时候,如果使用梯度下降(GD or SGD)或者梯度上升(GA or SGA),可能收敛 ...
- Machine Learning Algorithms Study Notes(6)—遗忘的数学知识
机器学习中遗忘的数学知识 最大似然估计( Maximum likelihood ) 最大似然估计,也称为最大概似估计,是一种统计方法,它用来求一个样本集的相关概率密度函数的参数.这个方法最早是遗传学家 ...
随机推荐
- photoshop 笔记
替换颜色 (图像)—(调整)—(替换颜色)—点下你想换掉的绿色----拖动下方的滑 块—(色相)拖到最大—(饱合度)调到最小----(明度)调到最大 OK 发现对你不想变色的图像稍微有点影响,但只是一 ...
- Servlet拓展
一. 概念 1.Servlet(Server Applet)是Java Servlet的简称,称为小服务程序或服务 连接器,用Java编写的服务器端程序,主要功能在于交互式地浏览和修改数据, ...
- Running Elixir in Docker Containers
转自:https://www.poeticoding.com/running-elixir-in-docker-containers/ One of the wonderful things abou ...
- C#遍历菜单项
(1)横向遍历 ToolStripMenuItem foreach (ToolStripMenuItem con in this.MainMenuStrip.Items) { ...
- 让使用SQLite的.NET应用自适应32位/64位系统
如果一个.NET应用要自适应32位/64位系统,只需要在项目的“目标平台”设置为“Any CPU”.但是如果应用中使用了SQLite,情况就不同了. SQLite的.NET开发包来自是System.D ...
- MongoDB之 写安全(Write Concern)
MongoDB Write Concern,简称MongoDB写入安全机制,是一种客户端设置,用于控制写入安全的级别.Write Concern 描述了MongoDB写入到mongod单实例,副本集, ...
- java 同步代码块与同步方法
同步代码块 synchronized (obj) { // 代码块 } obj 为同步监视器,以上代码的含义为:线程开始执行同步代码块(中的代码)之前,必须先获得对同步监视器的锁定. 代码块中的代码是 ...
- Golang client绑定本地IP和端口
有时需要指定网络通信时本地使用的IP地址和端口号. 在Go语言中可通过定义 Dialer 中LocalAddr 成员实现. Dialer结构定义如下: // A Dialer contains opt ...
- Pyhanlp自然语言处理中的新词识别
新词发现 本“新词发现”模块基于信息熵和互信息两种算法,可以在无语料的情况下提取一段长文本中的词语,并支持过滤掉系统中已存在的“旧词”,得到新词列表. 调用方法 静态方法 一句话静态调用接口已经封装到 ...
- SpringBoot进阶之web进阶
1.表单验证: 实体类添加: @Min(value = 18 ,message = "未成年少女禁止入内!")最小值限制为18,如果小于18则返回message中的信息 注入校验, ...
