Logistic Regression – Geometric Intuition

Everybody who has taken a machine learning course probably knows the geometric intuition behind a support vector machine (SVM, great book): A SVM is a large margin classifier. In other words, it maximizes the geometric distance between the decision boundary and the classes of samples. Often you’ll find plots similar to this one:

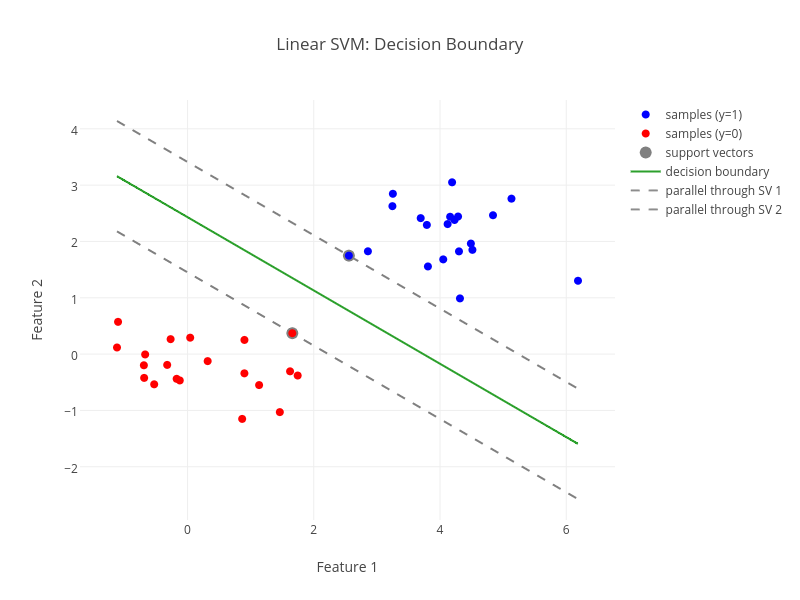
But what about logistic regression? What is the geometric intuition behind it and how does it compare to linear SVMs? Let’s find out.

Geometric intuition behind logistic regression

First, a quick reminder about the definition of the logistic function, given features:

With that out of the way, let’s dive into the geometric aspects of logistic regression, starting with a toy example of only one feature:

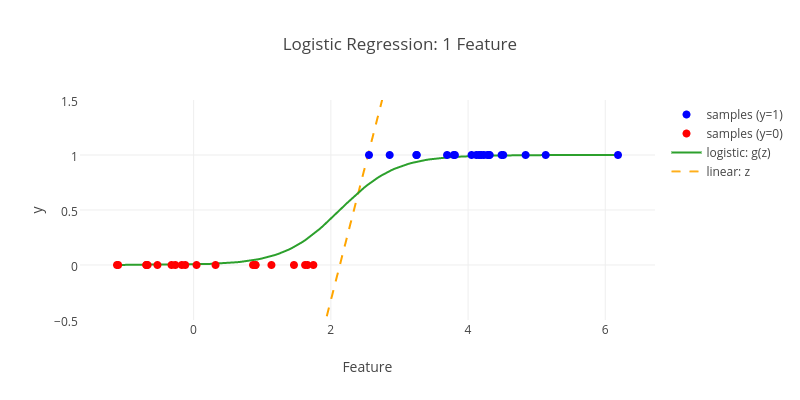
The blue samples of our feature data belong to class , while the red dots are supposed to get assigned to . As we can see in the figure above, our data is fully separable and the logistic regression is able to demonstrate this property. From a geometric perspective, the algorithm essentially adds a new dimension for our dependent variable and fits a logistic function to the arising two-dimensional data in such a way that it separates the samples as good as possible within the range of . Once we have such a fitted curve, the usual method of prediction is to assign to everything and vice versa.

When thinking about logistic regression, I usually have its tight connection to linear regression somewhere in the back of my head (no surprise, both have “regression” as part of their names). Therefore, I was wondering what the line would look like and added it to the plot. As we can easily see, differs significantly from the potential result of a linear regression for the given input data. While that was to be expected, I think it’s still nice to confirm it visually.

Note two details of the plot: For one, the logistic curve is not as steep as you might expect at first. This is due to the use of regularization, which logistic regression basically can’t live without. Second, for and not, as my intuition initially suggested, for . Not sure if this is particularly helpful, but I find it interesting nonetheless.

So far, so good. But what happens when we introduce an additional dimension? Let’s have a look at such a two feature scenario (feel free to pinch and zoom the plot):

What we see is the surface of the fitted logistic function for a classification task with two features. This time, instead of transforming a line to a curve, the equivalent happened for a plane. To make it easier to understand how to carry out predictions given such a model, the following plot visualizes the data points projected onto the surface of the logistic regression function:

Now we can again make decisions for our class based on a threshold , which usually is :

So much about the geometric intuition behind logistic regression. Let’s see how that compares to linear SVMs.

Comparison of logistic regression to linear SVM

First of all, notice that with logistic regression we can use the value of a sample as a probability estimate for . The responsive 3D-plots above created with the help of plotly’s fantastic library illustrate this property of logistic regression very well. I have yet to come across a real-world classification task where such probability estimates are not at least somewhat useful. Alas, SVMs (in their original version) aren’t able to provide them. Due to the way the model works, all it can tell you is whether a sample belongs to class or not.

I think at this point the most effective way of comparing logistic regression to linear SVM geometrically, is to add the decision boundary of logistic regression to the initial figure of the post. To make this happen, we need to project the decision boundary of the three-dimensional plot above onto the two-dimensional feature space. Doing so, we end up with the following figure:

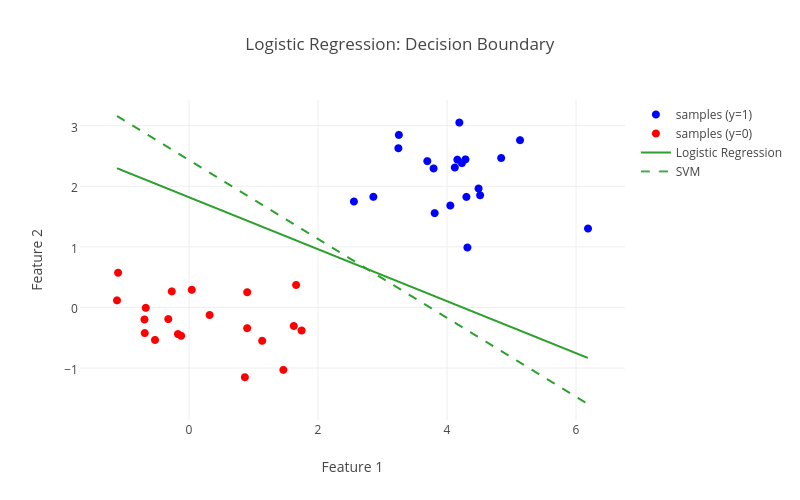
As we can see, the logistic regression does not follow the same large margin characteristic as a linear SVM. I’ll leave it to you to decide which is the better fit for the given data.

If you’d like to know further differences between logistic regression and linear SVMs aside from the geometrically motivated ones mentioned here, have a look at the excellent answers on quora.

The code for generating the plots of this post can be found on github.