Java的二分搜索树

定义

二分搜索树是二叉树(不包含重复元素)。

二分搜索树的每个节点的值，大于左子树的所有节点的值，小于其右子树的所有节点的值。

每一棵子树也是二分搜索树。

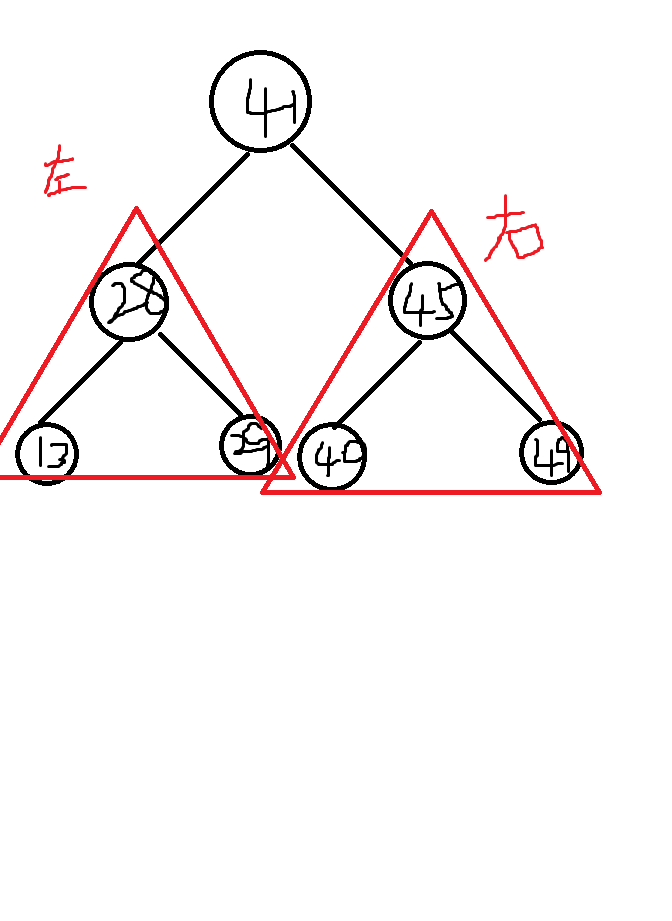
二叉树搜索树必须要有比较，继承Comparable类

插入元素

package com.dsideal;

public class BST<E extends Comparable<E>> {

    private class Node
    {
        private E e;
        //左右孩子
        private Node left,right;

        public Node(E e)
        {
            this.e = e;
            left = null;
            right = null;
        }

    }
    //根节点
    private Node root;
    //二叉树元素个数
    private int size;

    private BST()
    {
        root = null;
        size = 0;
    }

    //二叉树有几个节点
    public int size()
    {
        return size;
    }

    //二叉树是否为空
    public boolean isEmpty()
    {
        return size == 0;
    }

    public void add(E e)
    {
        root = add(root,e);
    }

    //向根添加元素
    private Node add(Node node,E e)
    {
        if(node == null)
        {
            size ++;
            return new Node(e);
        }

        if (e.compareTo(node.e) < 0)
        {
            node.left = add(node.left,e);
        }else if(e.compareTo(node.e) > 0)
        {
            node.right = add(node.right,e);
        }

        return node;
    }

}

二分搜索树的前序遍历，访问该节点是在左右子树之前。

private void preOrder(Node node)
    {
        if (node == null)
        {
            return;
        }
        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

二分搜索树的中序遍历，结果是排序的。

 //二分搜索树的中序排序
    public void inOrder()
    {
        inOrder(root);
    }

    private void inOrder(Node node)
    {
        if (node == null)
        {
            return;
        }
        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

二分搜索树的后序遍历

    //二分搜索树的后序遍历
    public void postOrder()
    {
        preOrder(root);
    }

    public void postOrder(Node node)
    {
        if (node == null)
        {
            return;
        }
        preOrder(node.left);
        preOrder(node.right);
        System.out.println(node.e);
    }

二分搜索树前序遍历非递归实现

    public void preOrderNR()
    {
        Stack<Node> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty())
        {
            Node cur = stack.pop();
            System.out.println(cur.e);
            if (cur.right != null)
            {
                stack.push(cur.right);
            }
            if (cur.left != null)
            {
                stack.push(cur.left);
            }
        }
    }

二分搜索树的层序遍历，最短路径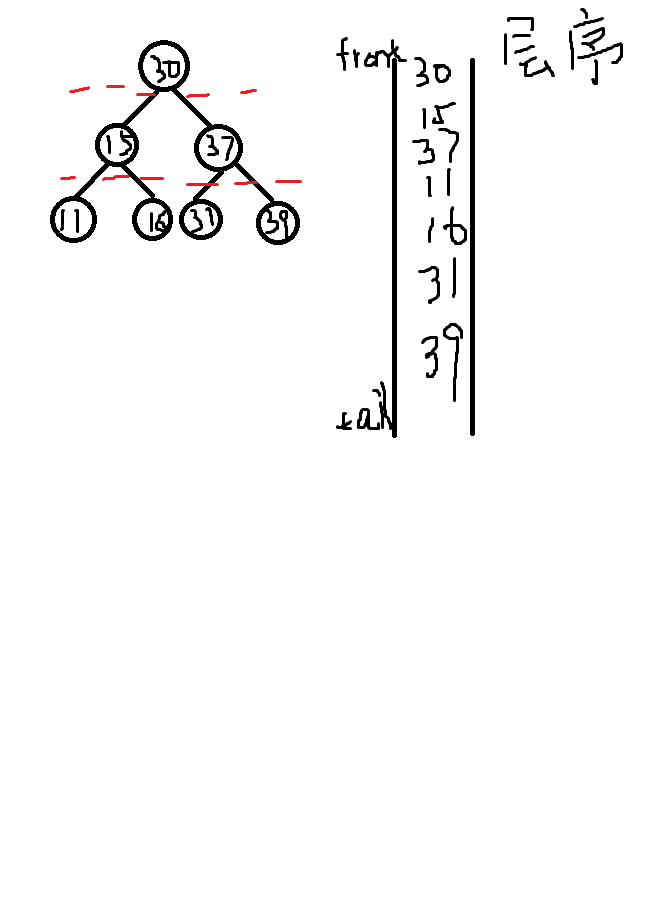

public void levelOrder()
    {
        Queue<Node> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty())
        {
            Node cur = queue.remove();
            System.out.println(cur.e);
            if (cur.left != null)
            {
                queue.add(cur.left);
            }
            if (cur.right != null)
            {
                queue.add(cur.right);
            }
        }
    }

重写toString

@Override
    public String toString()
    {
        StringBuffer res = new StringBuffer();
        generateBSTString(root,0,res);
        return res.toString();
    }

    private void generateBSTString(Node node, int depth, StringBuffer res)
    {
        if (node == null)
        {
            res.append(generateBSTString(depth) + "null\n");
            return;
        }
        res.append(generateBSTString(depth) + node.e + "\n");
        generateBSTString(node.left,depth + 1,res);
        generateBSTString(node.right,depth + 1,res);
    }

    public String generateBSTString(int depth)
    {
        StringBuffer res = new StringBuffer(" ");
        for (int i = 0; i < depth; i++) {
            res.append("--");
        }
        return res.toString();
    }

删除最大值和最小值

    //二分数的最大值
    public E maxNode()
    {
        if (isEmpty())
        {
            throw new IllegalArgumentException("BST is empty");
        }
        return maxNode(root).e;
    }

    private Node maxNode(Node node)
    {
        if (node.right == null)
        {
            return node;
        }
        return maxNode(node.right);
    }
    //二分数的最小值
    public E minNode()
    {
        if (isEmpty())
        {
            throw new IllegalArgumentException("BST is empty");
        }
        return minNode(root).e;
    }

    private Node minNode(Node node)
    {
        if (root.left == null)
        {
            return node;
        }
        return minNode(node.left);
    }

    public E removeMax()
    {
        E cur = maxNode();
        root = removeMax(root);
        return cur;
    }
    //删除最大值,返回根
    private Node removeMax(Node node)
    {
        if (node.right == null)
        {
            Node rightNode = node.left;
            node.left = null;
            size --;
            return rightNode;
        }
        node.right = removeMax(node.right);
        return node;
    }

    public E removeMin()
    {
        E cur = minNode();
        root = removeMin(root);
        return null;
    }

    private Node removeMin(Node node)
    {
        if (node.left == null)
        {
            Node leftNode = node.right;
            node.right = null;
            size--;
            return leftNode;
        }
        node.left = removeMin(node.left);
        return node;
    }

删除节点

    //删除二分搜索树的节点
    private Node remove(Node node, E e)
    {
        if (node == null)
        {
            return null;
        }
        if (e.compareTo(node.e) < 0)
        {
            node.left = remove(node.left,e);
            return node;
        }else if (e.compareTo(node.e) > 0)
        {
            node.right = remove(node.right,e);
            return node;
        }else{
            if (node.right == null)
            {
                Node leftNode = node.left;
                node.left = null;
                size --;
                return leftNode;
            }
            if (node.left == null)
            {
                Node righNode = node.right;
                node.right = null;
                size--;
                return righNode;
            }

            Node successor = minNode(node.right);
            successor.right = removeMin(node.right);
            successor.left = node.left;

            node.right = node.left = null;
            return successor;
        }

    }