poj 2142 The Balance
| Time Limit: 5000MS | Memory Limit: 65536K | |
Description
You are asked to help her by calculating how many weights are required.
Input
The end of the input is indicated by a line containing three zeros separated by a space. It is not a dataset.
Output
- You can measure dmg using x many amg weights and y many bmg weights.
- The total number of weights (x + y) is the smallest among those pairs of nonnegative integers satisfying the previous condition.
- The total mass of weights (ax + by) is the smallest among those pairs of nonnegative integers satisfying the previous two conditions.
No extra characters (e.g. extra spaces) should appear in the output.
Sample Input
700 300 200
500 200 300
500 200 500
275 110 330
275 110 385
648 375 4002
3 1 10000
0 0 0
Sample Output
1 3
1 1
1 0
0 3
1 1
49 74
3333 1
Source
#include<cstdio>
#include<algorithm>
using namespace std;
int exgcd(int a,int b,int &x,int &y)
{
if(!b) {x=; y=; return a;}
int d=exgcd(b,a%b,x,y);
int t=x; x=y; y=t-a/b*y;
return d;
}
int main()
{
int a,b,c;
while(scanf("%d%d%d",&a,&b,&c)!=EOF)
{
if(!a&&!b&&!c) return ;
bool f=false;
if(a<b) swap(a,b),f=true;
int x,y;
int d=exgcd(a,b,x,y);
int x0=c/d*x,y0=c/d*y;
int t=d*y0/a;
a/=d; b/=d;
int add=0x7fffffff,mul=0x7fffffff;
int ansx,ansy;
for(int i=t-;i<=t+;i++)
{
x=x0+i*b; y=y0-i*a;
if(x<) x=-x;
if(y<) y=-y;
if(x+y<add)
{
add=x+y;
ansx=x;ansy=y;
mul=a*x+b*y;
}
else if(x+y==add)
{
if(a*x+b*y<mul)
{
ansx=x;ansy=y;
mul=a*x+b*y;
}
}
}
if(!f) printf("%d %d\n",ansx,ansy);
else printf("%d %d\n",ansy,ansx);
}
}
poj 2142 The Balance的更多相关文章
- POJ.2142 The Balance (拓展欧几里得)
POJ.2142 The Balance (拓展欧几里得) 题意分析 现有2种质量为a克与b克的砝码,求最少 分别用多少个(同时总质量也最小)砝码,使得能称出c克的物品. 设两种砝码分别有x个与y个, ...
- POJ 2142 The Balance(exgcd)
嗯... 题目链接:http://poj.org/problem?id=2142 AC代码: #include<cstdio> #include<iostream> using ...
- POJ 2142 The Balance【扩展欧几里德】
题意:有两种类型的砝码,每种的砝码质量a和b给你,现在要求称出质量为c的物品,要求a的数量x和b的数量y最小,以及x+y的值最小. 用扩展欧几里德求ax+by=c,求出ax+by=1的一组通解,求出当 ...
- POJ 2142 The Balance (解不定方程,找最小值)
这题实际解不定方程:ax+by=c只不过题目要求我们解出的x和y 满足|x|+|y|最小,当|x|+|y|相同时,满足|ax|+|by|最小.首先用扩展欧几里德,很容易得出x和y的解.一开始不妨令a& ...
- POJ 2142 The balance | EXGCD
题目: 求ax+by=c的一组解,使得abs(x)+abs(y)尽量小,满足前面前提下abs(ax)+abs(by)尽量小 题解: exgcd之后,分别求出让x尽量小和y尽量小的解,取min即可 #i ...
- POJ - 2142 The Balance(扩展欧几里得求解不定方程)
d.用2种砝码,质量分别为a和b,称出质量为d的物品.求所用的砝码总数量最小(x+y最小),并且总质量最小(ax+by最小). s.扩展欧几里得求解不定方程. 设ax+by=d. 题意说不定方程一定有 ...
- POJ 2142 - The Balance [ 扩展欧几里得 ]
题意: 给定 a b n找到满足ax+by=n 的x,y 令|x|+|y|最小(等时令a|x|+b|y|最小) 分析: 算法一定是扩展欧几里得. 最小的时候一定是 x 是最小正值 或者 y 是最小正值 ...
- The Balance POJ 2142 扩展欧几里得
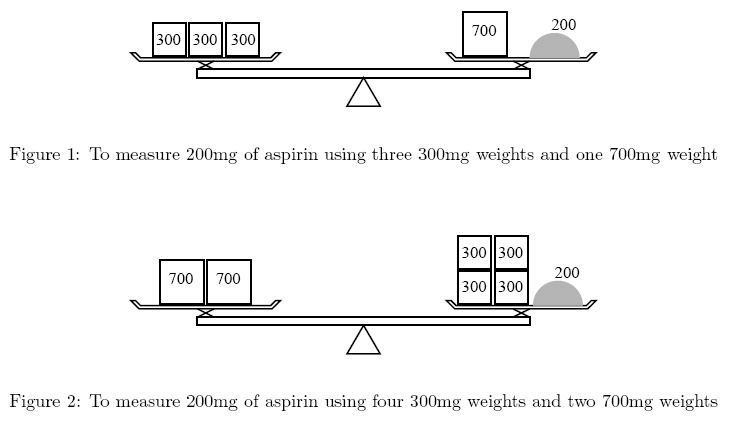
Description Ms. Iyo Kiffa-Australis has a balance and only two kinds of weights to measure a dose of ...
- POJ 2142:The Balance
The Balance Time Limit: 5000MS Memory Limit: 65536K Total Submissions: 4781 Accepted: 2092 Descr ...
随机推荐
- Xcode 9.0 新增功能大全
Xcode是用于为Apple TV,Apple Watch,iPad,iPhone和Mac创建应用程序的完整开发人员工具集.Xcode开发环境采用tvOS SDK,watchOS SDK,iOS SD ...
- C#总结(六)EventBus事件总线的使用-自己实现事件总线
在C#中,我们可以在一个类中定义自己的事件,而其他的类可以订阅该事件,当某些事情发生时,可以通知到该类.这对于桌面应用或者独立的windows服务来说是非常有用的.但对于一个web应用来说是有点问题的 ...
- 解决Android Studio 3.0导入module依赖后unable to merge index
解决Android Studio 3.0导入module依赖后unable to merge index 项目需要使用im, 在项目里导入了腾讯im的几个module依赖, 项目无法编译, 报错una ...
- UML那些事
什么是UML?它的全名:Unified Modeling Language,统一建模语言.最近我用到了uml,顺便重温了下这些知识.知乎上有一个讨论话题:uml还有用吗?这个讨论挺有意思的,看完后,受 ...
- java ssm框架实现分页功能 (oracle)
java web 实现分页功能 使用框架:ssm 数据库:oracle 话说 oracle 的分页查询比 mysql 复杂多了,在这里简单谈一下: 查询 前十条数据: SELECT * FROM( S ...
- windows下编译caffe报错:error MSB4062: 未能从程序集 E:\NugetPackages\OpenCV.2.4.10\......的解决办法
参考博客:http://blog.csdn.net/u013277656/article/details/75040459 在windows上编译caffe时,用vs打开后会自动加载还原NugetPa ...
- input依次输入密码
原理: 一个真正的可以输入的input框,opacity: 0,设定位层级:(视图不可见的) 再来6(n)个input,readyonly,用来显示,type为password,设置好样式:(视图可见 ...
- Shiro【授权、整合Spirng、Shiro过滤器】
前言 本文主要讲解的知识点有以下: Shiro授权的方式简单介绍 与Spring整合 初始Shiro过滤器 一.Shiro授权 上一篇我们已经讲解了Shiro的认证相关的知识了,现在我们来弄Shiro ...
- three.js 实现全景以及优化(2)
继昨天全景实现后,再做了一个全景图切换实验; code:https://github.com/Thinkia/threejs_/blob/master/test/test1-panorama/inde ...
- Android库项目中的资源ID冲突
1.前言 Android Studio对模块化开发提供的一个很有用的功能就是可以在主项目下新建库项目(Module),但是在使用库项目时却有一个问题就是资源ID冲突,因为编译时SDK会自动帮我们处理这 ...
