【无语凝噎（wordless）】

·题目：

        西施与范蠡泛舟而去……不对，场景不对，咳咳。在甄嬛前往蓬莱洲之前，她与皇上在碧桐书院告别。为了这可能会长达数月的离别，两个人都似乎有很多话要对对方说，却都无语凝噎。这时，皇上突然发话：“嬛嬛啊(桓桓？)，既然你我都说不出话来，那这时间也不好打发，我们来数三角形吧。”为了满足皇上突发而来的童趣，甄嬛欣然陪同了。可这……纸上是一张n*m的格子方阵，即有(n+1)*(m+1)个格点。每个格子都是边长为1的正方形。而他们要数的，则是任取3个格点作为三角形的顶点所形成的直角三角形且该三角形面积为s/2的个数。甄嬛数的头都晕了，她现在只想知道满足条件的三角形个数 mod 1000000007。

输入格式：第一行3个正整数n，m，s, 意义如题

输出格式：仅一个整数，为甄嬛与满足条件的三角形个数 mod (10^9+7)

样例输入：1 1 1

样例输出：4

数据范围：

对于10%的数据：n<=10
对于另外40%的数据：s为质数
对于100%的数据：1<=n,m,s<=10⁸

时间限制： 1S

空间限制： 128M

·题目混乱，述大意：

     给定长度为n*m的相同正方形方格组成的棋盘，求出使用格点组成的三角形个数，答案取模1000000007。(n,m<=10⁸)。

·分析：

      在草稿纸上画图时容易发现一些普遍规律和特例，此时大米饼认为应该先里找出总体的方法，再进行特例的处理(如去重),这样很美妙。一个非常简单的思路是，设这个三角形的边长为a,b,那么在棋盘上就有如下摆法：

    

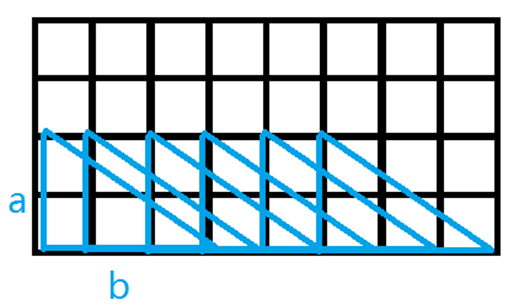
     同时要算上棋盘旋转90^o后的情况，不要忘记一个三角形可以在同一个长方形里有四种摆法，所以对于这个形状的三角形的个数P可以表示为:

     P=(n-a+1)*(m-b+1)*4+(n-b+1)*(m-a+1)*4

     读题一会儿后意识到一个问题是三角形的边可以是斜着的。上文的天真方法连正确答案都无法得出：

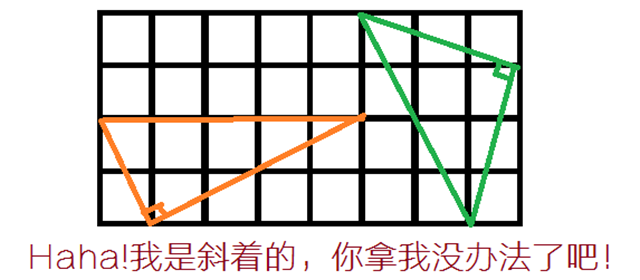
     在经历初中数学洗礼的我们开始回想起中考时的一些琐碎，发现好像很多几何题都是这样子的——有关相似直角三角形。清晰地发现，这些三角形的直角边无非是由两个相似的直角三角形的斜边组成：

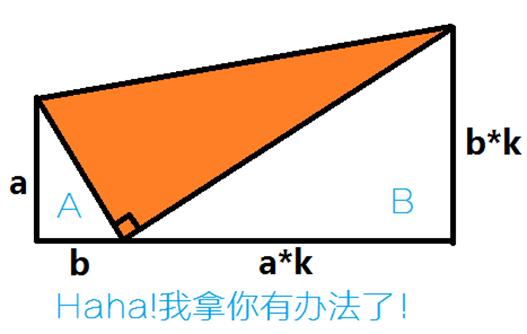
     依照这个思路，做一些便于代码书写的分析。首先使用a,b表示出橙色三角形的面积S=(a²+b²)*k[注意,k不一定偏要为整数，想一想，不为什么]。我们看一看数据范围：n,m<=100000000,开方后为10000，说明最坏情况循环下循环次数：10⁸。不过，这里我们需要保证a,b,ak,bk均为整数，也就是分解数——“与分解有关的时间复杂度稳定性很差”，我们可以直接暴力枚举a,b，找到所有满足面积公式条件的二元组(a,b)，并由此可以推出对应的k值。

     与此同时，一个更加振奋人心的消息——上文那种边与格子平行的情况可以看做(a,b)其中一个为0的情况，所以我们争取一起处理。

     这样看来，似乎只需要进行一个二重循环枚举a,b然后使用类似于上文的天真方法计算答案就可以了。在激动之余，你发现还有一些特殊情况。

     为了有序性和避免重复，我们规定枚举二元组(a,b)必须满足k的值大于等于1。我们先列出一般情况的答案计算方法。对于一组(a,b)构成面积为S的三角形的个数P计算方法：
    

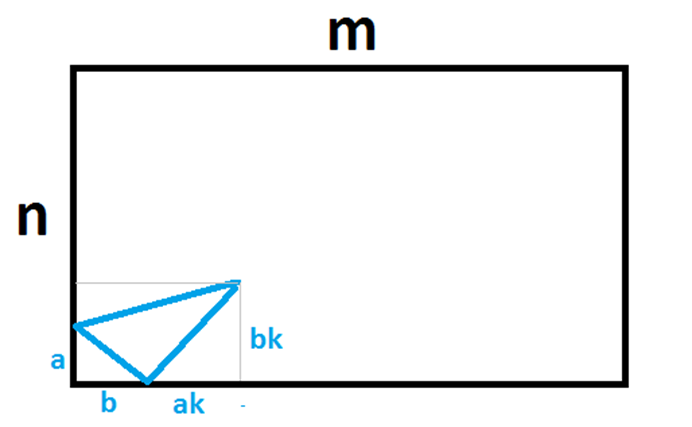
    对于这个三角形，我们只需要求出其所在的最小矩形的长宽就可以了。由于a,b的大小关系不确定。所以：

     宽长度为：max(a,bk),长长度为：b+ak

   我们设长宽分别为p,q,那么S的个数为：

     P=(n-p+1)*(m-q+1)*4+(n-p+1)*(m-q+1)*4

    最后我们着眼于两种特殊情况的处理：

   [1] k==1:

      由于a,b大小不定，所以如果(a,b)满足,那么(b,a)也是合法的，此时相当于计算了8次，但是我们发现，由于k值为1，所以相似三角形为等腰，重复计算了，所以处理方式是除以二。

   [2] a==0||b==0：

     这表明是一个直角边和格子边平行的直角三角形。设u>0,如果二元组(u,0)合法，那么(0,u)同样合法，但是！(u,0),(0,u)形成的三角形形状完全相同，而(u,v),(v,u)[v>0]形成的三角形形状是相同或者不同，但是相同的情况被[1]的处理方式而排除，可是(u,0)(0,u)的重复计算没有排除。随意处理方式也是除以二。

     考试结束后其实很多STD的写法是将(a,b)中是否有0进行分开计算，这样更容易理解。但是追求更深刻理解和短码的大米饼毫不犹豫地视作一种情况讨论。代码来啦：

 #include<stdio.h>
 #include<algorithm>
 #define ll long long
 #define M 1000000007
 #define go(i,a,b) for(ll i=a;i<=b;i++)
 using namespace std;
 ll n,m,s,t,res,ans,A,B,T,X,Y;
 ll Cal(ll a,ll b){return max(1ll*,n-a+)*max(1ll*,m-b+)%M;}
 int main()
 {
     scanf("%lld%lld%lld",&n,&m,&s);
     go(a,,M){if(a*a>s)break;
     go(b,a?:,M){if((res=a*a+b*b)>s)break;
         if(1ll*a*s%res||1ll*b*s%res)continue;
         A=a*s/res,B=b*s/res;T=res==s?:;
         if(a==||b==)T/=;X=b+A;Y=max(a,B);
         (ans+=T*Cal(X,Y)+T*Cal(Y,X))%=M;
     }}printf("%lld",(ans%M+M)%M);return ;
 }//Paul_Guderian

如果青春是一捧鲜花，我愿把它洒给你，

如果生命是一场燃烧的旧梦，

我愿在梦醒前燃烬……   ————汪峰《忧郁的眼睛》