[NOIp 2014]联合权值

Description

无向连通图G 有n 个点，n - 1 条边。点从1 到n 依次编号，编号为 i 的点的权值为W i ，每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ，若它们的距离为2 ，则它们之间会产生Wu×Wv 的联合权值。

请问图G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

Input

输入文件名为link .in。

第一行包含1 个整数n 。

接下来n - 1 行，每行包含 2 个用空格隔开的正整数u 、v ，表示编号为 u 和编号为v 的点之间有边相连。

最后1 行，包含 n 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。

Output

输出文件名为link .out 。

输出共1 行，包含2 个整数，之间用一个空格隔开，依次为图G 上联合权值的最大值

和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对10007 取余。

Sample Input

Sample Output

20 74

HINT

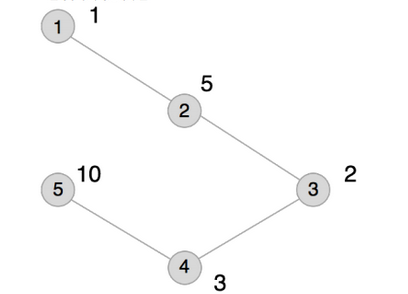
本例输入的图如上所示，距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30% 的数据，1 < n≤ 100 ；

对于60% 的数据，1 < n≤ 2000；

对于100%的数据，1 < n≤ 200 , 000 ，0 < wi≤ 10, 000 。

题解

抓取有用信息:

1、$n$个点,$n-1$条边,实际上是一棵树;

2、点$(u,v)$算答案当且仅当距离为$2$(仔细审题,不是$≥2$),那就是两个点中间隔了一个点。

60分算法:

1、枚举中间点$x$,然后把与$x$相连的点取出来,然后一一枚举它们形成的点对即可;

2、时间复杂度$O(n^2)$。

100分算法:

1、考虑优化$60$分算法中统计的那部分,求最大值的话,权值最大的点和权值次大的点的乘积,就是经过这个点的最大权值点对;

2、求和的话可以这样考虑:
$$ans=a1a2+(a1+a2)*a3+(a1+a2+a3)*a4......$$

3、所以我们可以枚举每一个元素,并将当前元素的权值与之前所有元素的权值和相乘,然后把所有的结果加起来即可。

4、时间复杂度$O(n)$。

注意取模。

 #include <set>

 #include <map>

 #include <ctime>

 #include <cmath>

 #include <queue>

 #include <stack>

 #include <vector>

 #include <cstdio>

 #include <string>

 #include <cstring>

 #include <cstdlib>

 #include <iostream>

 #include <algorithm>

 #define LL long long

 #define Max(a, b) ((a) > (b) ? (a) : (b))

 #define Min(a, b) ((a) < (b) ? (a) : (b))

 using namespace std;

 const int MOD = ;

 const int N = ;

 struct tt{

     int to, next;

 }edge[N*+];

 int path[N+], top;

 int n, u, v;

 int w[N+];

 LL maxans = ;

 int tolans;

 void add(int u, int v){

     edge[++top].to = v;

     edge[top].next = path[u];

     path[u] = top;

 }

 int main(){

     scanf("%d", &n);

     for (int i = ; i < n; i++){

   　　  scanf("%d%d", &u, &v);

  　　   add(u, v);

    　　 add(v, u);

     }

     for (int i = ; i <= n; i++)

    　　 scanf("%d", &w[i]);

     for (int u = ; u <= n; u++){

         LL max1 = , max2 = ;

     　　int tol = ;

   　　  for (int i = path[u]; i; i=edge[i].next){

     　　    LL c = w[edge[i].to];

       　　  tolans = (tolans+tol*c) %MOD;

         　　tol = (tol+c)%MOD;

        　　 if (c > max2) swap(max2, c);

        　　 if (max2 > max1) swap(max1, max2);

        　　 maxans = Max(maxans, (LL)max1*max2);

    　　 }

     }

     printf("%lld %d\n", maxans, (*tolans)%MOD);

     return ;

 }