附录D——自动微分（Autodiff）

本文介绍了五种微分方式，最后两种才是自动微分。

前两种方法求出了原函数对应的导函数，后三种方法只是求出了某一点的导数。

假设原函数是$f(x,y) = x^2y + y +2$，需要求其偏导数$\frac{\partial f}{\partial x}$和$\frac{\partial f}{\partial y}$，以便应用于梯度下降等算法。

1、手工求导

该方法比较简单，就是自备纸笔，应用基本的求导规则，以及链式求导法则，人工求导。缺点是对于复杂函数容易出错。幸运的是，这一计算过程可由计算机帮我们完成，这就是符号微分。

2、符号微分（Symbolic Differentiation）

如图D-1所示，使用符号微分的方法，计算函数$g(x,y) = 5 + xy$的偏导数。该图左侧代表函数$g(x,y)$，右侧代表$g(x,y)$关于$x$的偏导数$\frac{\partial g}{\partial x} = 0 + (0 \times x + y \times 1) = y$（同样的，可以求得$\frac{\partial g}{\partial y}$）。

图D-1 符号微分

该算法首先求叶子节点关于$x$的偏导数，然后沿着树向上，求得其他节点关于自变量的偏导数。这与手工求导所使用的规则是一样的。

如果函数复杂，该算法生成的树将十分庞大，性能不高。而且无法对很随意的代码求导，例如：

def my_func(a, b):
    z = 0
    for i in range(100):
        z = a * np.cos(z + i) + z * np.sin(b - i)
    return z 

3、数值微分（Numerical Differentiation）

这是根据导数的定义来求解的。函数$h(x)$在$x_0$点的导数为：

$h'(x) = \lim_{\varepsilon \rightarrow 0} \frac{h(x_0 + \varepsilon) - h(x_0)}{\varepsilon}$

我们取一个很小的$\varepsilon$，带入公式进行计算即可。该方法所得结果不够精确，参数过多时计算量也比较大。但是计算起来很简单，可用于校验手工算出的导数是否正确。

如果有1000个参数，至少需要调用$h(x)$1001词，来求得所有偏导数。

4、前向自动微分（Forward-Mode Autodiff）

该算法依赖一个虚数（dual numbers，这让我想起来oracle的虚表。难度dual可以表示虚无的意思？） $\varepsilon$，满足$\varepsilon^2 = 0$但是$\varepsilon \neq 0$（姑且理解为一阶无穷小吧）。

由于$\varepsilon$是无穷小，因此满足$h(a + b \varepsilon) = h(a) + b \times h'(a)\varepsilon$。因此，算出$h(a + \varepsilon) $可以同时得到$h(a)$和$h'(a)$，如图D-2所示。

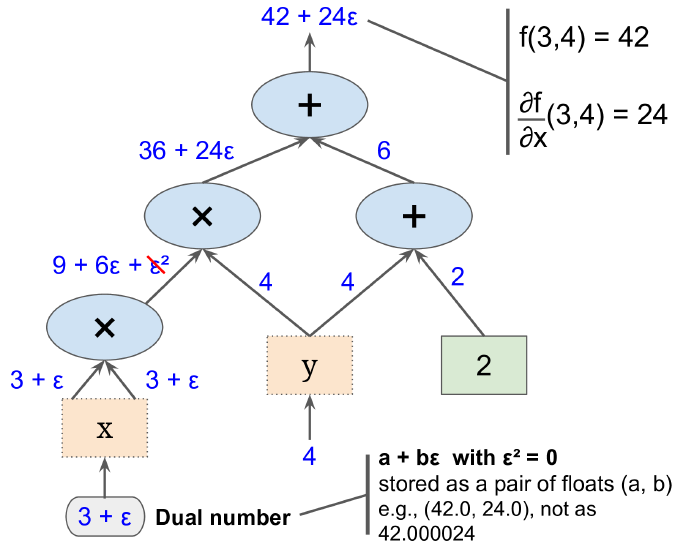
图D-2 前向自动微分

上图值计算了$\frac{\partial f}{\partial x}(3,4)$，同样的方法可以算的$\frac{\partial f}{\partial y}(3,4)$。

如果有1000个参数，需要遍历上图1000次，来求得所有偏导数。

5、反向自动微分（Reverse-Mode Autodiff）

这是TensorFlow所采用的自动微分算法。如图D-3所示，该算法首先前向（也就是从输入到输出）计算每个节点的值，然后反向（从输出到输入）计算所有的偏导数。

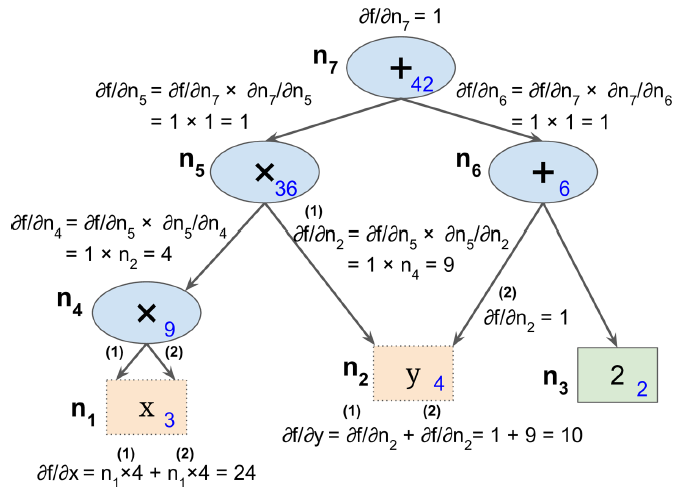
图D-3 反向自动微分

反向计算时应用链式求导法则：

$\frac{\partial f}{\partial x} = \frac{\partial f}{\partial n_i} \times \frac{\partial n_i}{\partial x}$

由于$n_7$就是输出节点，$f = n_7$，因此$\frac{\partial f}{\partial n_7} = 1$。

该算法强大且精确，尤其是输入很多，输出很少时。假如函数有10个输出（不管输入是1千，2万还是更多），求得所有偏导数需要对上图遍历11次。

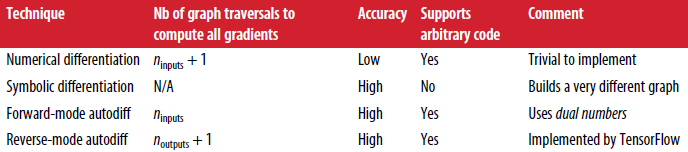
各个算法比较：