n-grama

一、N-Gram的原理(这个词出现在句子中出现的概率)

N-Gram是基于一个假设：第n个词出现与前n-1个词相关，而与其他任何词不相关。（这也是隐马尔可夫当中的假设。）整个句子出现的概率就等于各个词出现的概率乘积。各个词的概率可以通过语料中统计计算得到。假设句子T是有词序列w1,w2,w3...wn组成，用公式表示N-Gram语言模型如下：

P(T)=P(w1)*p(w2)*p(w3)***p(wn)=p(w1)*p(w2|w1)*p(w3|w1w2)***p(wn|w1w2w3...)

一般常用的N-Gram模型是Bi-Gram和Tri-Gram。分别用公式表示如下：

Bi-Gram:　　P(T)=p(w1|begin)*p(w2|w1)*p(w3|w2)***p(wn|wn-1)

Tri-Gram:　　P(T)=p(w1|begin1,begin2)*p(w2|w1,begin1)*p(w3|w2w1)***p(wn|wn-1,wn-2)

• 注意上面概率的计算方法：P(w1|begin)=以w1为开头的所有句子/句子总数；p(w2|w1)=w1,w2同时出现的次数/w1出现的次数。以此类推。（这里需要进行平滑）

二、N-Gram的应用

根据上面的分析，N-Gram（有时也称为N元模型）是自然语言处理中一个非常重要的概念，通常在NLP中，它主要有两个重要应用场景：

（1）、人们基于一定的语料库，可以利用N-Gram来预计或者评估一个句子是否合理。

（2）、另外一方面，N-Gram的另外一个作用是用来评估两个字符串之间的差异程度。这是模糊匹配中常用的一种手段。

1、N-gram在两个字符串的模糊匹配中的应用

首先需要介绍一个比较重要的概念：N-Gram距离。

（1）N-gram距离

它是表示，两个字符串s，t分别利用N-Gram语言模型来表示时，则对应N-gram子串中公共部分的长度就称之为N-Gram距离。例如：假设有字符串s，那么按照N-Gram方法得到N个分词组成的子字符串，其中相同的子字符串个数作为N-Gram距离计算的方式。具体如下所示：

字符串：s="ABC"，对字符串进行分词，考虑字符串首尾的字符begin和end，得到begin，A，B，C，end。这里采用二元语言模型，则有：（begin,A）、（A,B）、（B,C）、（C,end）。

字符串：t="AB"，对字符串进行分词，考虑字符串首尾的字符begin和end，得到begin，A，B，end。这里采用二元语言模型，则有：（begin,A）、（A,B）、（B,end）。

此时，若求字符串t与字符串s之间的距离可以用M-(N-Gram距离)=0。

然而，上面的N—gram距离表示的并不是很合理，他并没有考虑两个字符串的长度，所以在此基础上，有人提出非重复的N-gram距离，公式如下所示：

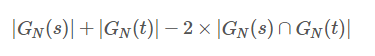
上面的字符串距离重新计算为：

　　　　　　4+3-2*3=1

2、N-Gram在判断句子有效性上的应用

假设有一个字符串s="ABC",则对应的BI-Gram的结果如下：（begin,A）、（A,B）、（B,C）、（C,end）。则对应的出现字符串s的概率为：

P(ABC)=P(A|begin)*P(B|A)*P(C|B)*P(end|C)。

3、N-Gram在特征工程中的应用

在处理文本特征的时候，通常一个关键词作为一个特征。这也许在一些场景下可能不够，需要进一步提取更多的特征，这个时候可以考虑N-Gram，思路如下：

以Bi-Gram为例，在原始文本中，以每个关键词作为一个特征，通过将关键词两两组合，得到一个Bi-Gram组合，再根据N-Gram语言模型，计算各个Bi-Gram组合的概率，作为新的特征。