hdu 1253 胜利大逃亡 (广搜)

题目链接

Problem Description

Ignatius被魔王抓走了,有一天魔王出差去了,这可是Ignatius逃亡的好机会.

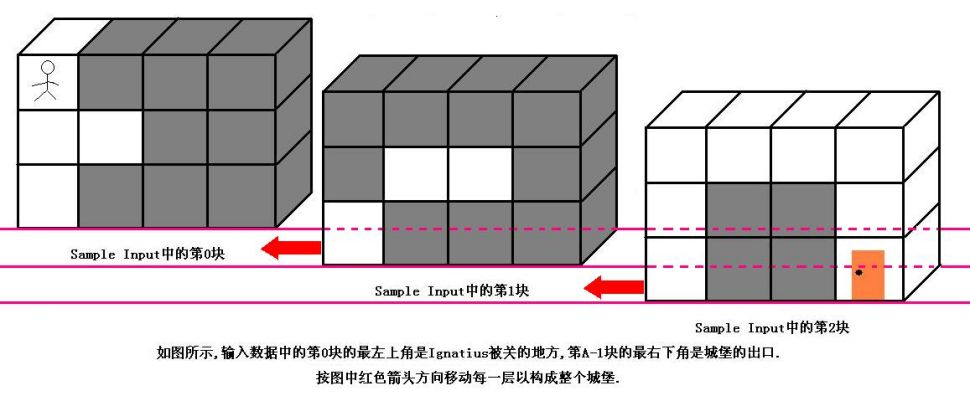
魔王住在一个城堡里,城堡是一个ABC的立方体,可以被表示成A个B*C的矩阵,刚开始Ignatius被关在(0,0,0)的位置,离开城堡的门在(A-1,B-1,C-1)的位置,现在知道魔王将在T分钟后回到城堡,Ignatius每分钟能从一个坐标走到相邻的六个坐标中的其中一个.现在给你城堡的地图,请你计算出Ignatius能否在魔王回来前离开城堡(只要走到出口就算离开城堡,如果走到出口的时候魔王刚好回来也算逃亡成功),如果可以请输出需要多少分钟才能离开,如果不能则输出-1.

Input

输入数据的第一行是一个正整数K,表明测试数据的数量.每组测试数据的第一行是四个正整数A,B,C和T(1<=A,B,C<=50,1<=T<=1000),它们分别代表城堡的大小和魔王回来的时间.然后是A块输入数据(先是第0块,然后是第1块,第2块......),每块输入数据有B行,每行有C个正整数,代表迷宫的布局,其中0代表路,1代表墙.(如果对输入描述不清楚,可以参考Sample Input中的迷宫描述,它表示的就是上图中的迷宫)

特别注意:本题的测试数据非常大,请使用scanf输入,我不能保证使用cin能不超时.在本OJ上请使用Visual C++提交.

Output

对于每组测试数据,如果Ignatius能够在魔王回来前离开城堡,那么请输出他最少需要多少分钟,否则输出-1.

Sample Input

1

3 3 4 20

0 1 1 1

0 0 1 1

0 1 1 1

1 1 1 1

1 0 0 1

0 1 1 1

0 0 0 0

0 1 1 0

0 1 1 0

Sample Output

11

分析：

特别简单的一个广搜的过程，就是走一个立方体的一个对角线的过程，中间毫无障碍物什么的阻碍，相对来说是比较简单的，但是在走的过程中要考虑道剪纸，不然的话可能会T。

代码：

#include<cmath>
#include<iostream>
#include<stdio.h>
#include<queue>
#include<string.h>
using namespace std;
int a,b,c,t;
int Map[55][55][55];
int vis[55][55][55];
struct Node
{
    int x,y,z;
    int step;
};
struct Node1
{
    int x,y,z;
} flg[]= {{0,0,1},{0,0,-1},{0,1,0},{0,-1,0},{1,0,0},{-1,0,0} };//六个方向走时对应的坐标变化
int abs(int x)//绝对值
{
    return x<0?-x:x;
}

int bfs( )
{
    Node Now,Next;
    Now.x=0;
    Now.y=0;
    Now.z=0;
    Now.step=0;
    queue<Node> q;
    q.push(Now);
    while(!q.empty())
    {
        Now=q.front();
        q.pop();
        if(Now.x==a-1&&Now.y==b-1&&Now.z==c-1&&Now.step<=t)
        {
            return Now.step;
        }
        for(int i=0; i<6; i++)
        {
            Next.x=Now.x+flg[i].x;
            Next.y=Now.y+flg[i].y;
            Next.z=Now.z+flg[i].z;
            if(Next.x>=0&&Next.x<a&&Next.y>=0&&Next.y<b&&Next.z>=0&&Next.z<c&&!Map[Next.x][Next.y][Next.z]&&!vis[Next.x][Next.y][Next.z])
            {
                Next.step=Now.step+1;
                vis[Next.x][Next.y][Next.z]=1;
                if(abs(Next.x-a+1)+abs(Next.y-b+1)+abs(Next.z-c+1)+Next.step>t)//由于行走只能朝6个固定方向，这里是对剩下时间里能否走到出口进行预判，如果走最短路径依然不能再规定时间内到达出口，明显是不行的,当然不加这个判断也能AC，只是比较消耗时间
                    continue;
                q.push(Next);
            }
        }
    }
    return -1;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        memset(Map,0,sizeof(Map));
        memset(vis,0,sizeof(vis));
        scanf("%d%d%d%d",&a,&b,&c,&t);
        for(int i=0; i<a; i++)
            for(int j=0; j<b; j++)
                for(int k=0; k<c; k++)
                    scanf("%d",&Map[i][j][k]);
        vis[0][0][0]=1;
        int ans=bfs();
        printf("%d\n",ans);
    }
    return 0;
}