D. GCD Counting（树上dp）

题目链接：http://codeforces.com/contest/1101/problem/D

题目大意：给你n个点，每个点都有权值，然后给你边的关系，问你树上的最大距离。（这里的最大距离指的是这条路径上的所有数最大gcd>1）。

 具体思路：首先，我们可以找出对于一个父亲节点，他和子节点能够在不是互素的前提下，对于他们每一个因子的个数。

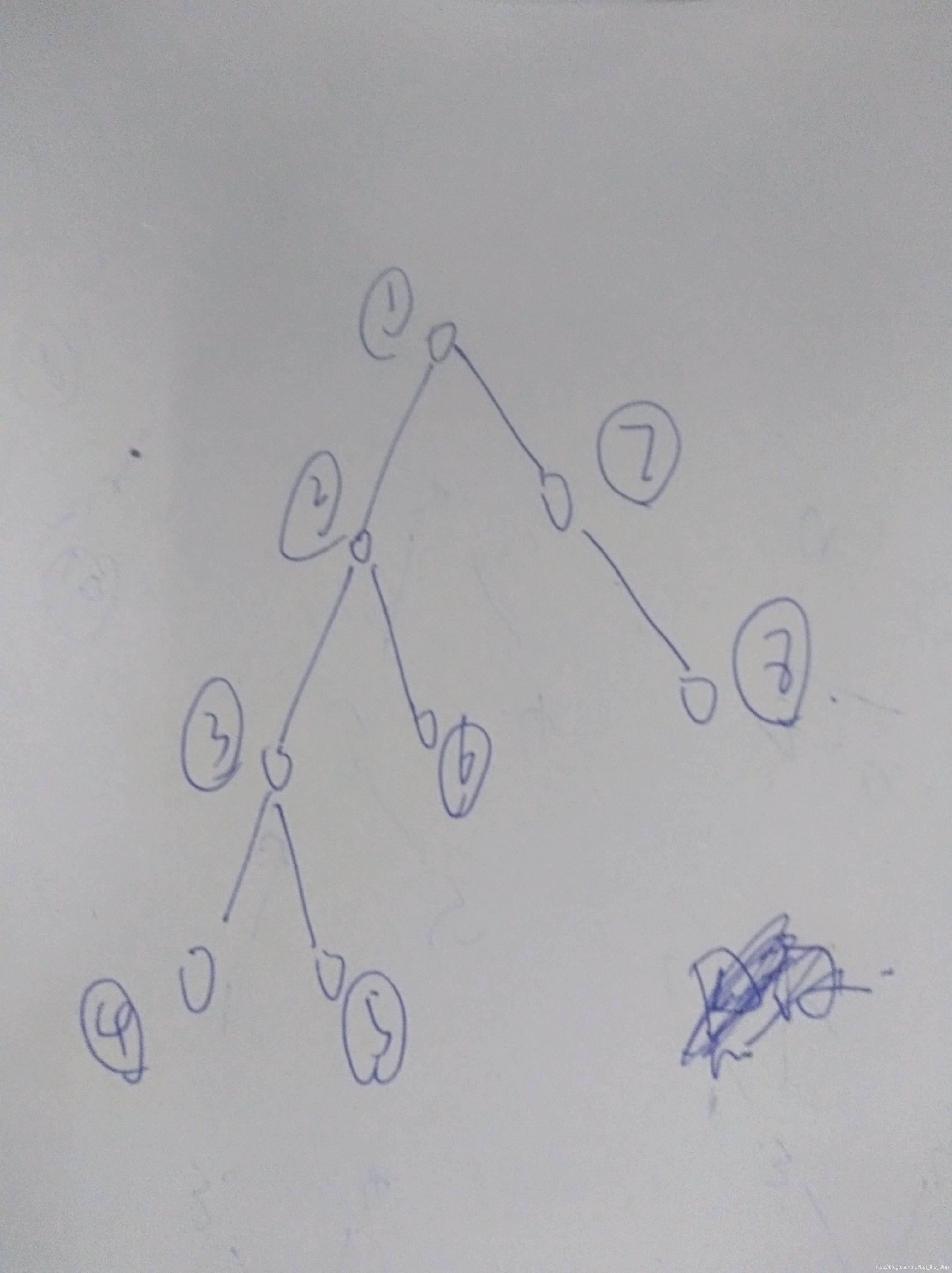
然后我们先dfs到底部，然后看他的每一个子节点之间产生的最大公因数是不是1，如果不是的话，我们就求这条路径上的最大值，在求最大值的时候，我们还是按照树的结构来，如图所示，从4号节点开始，4号节点更新之后会回到上一层，也就是3号节点，然后再求3号节点的所有因子和4号节点的因子是不是互素的，如果不是就从不是互素的这些状态里面找出一个最大值，然后在更新3号节点，这样更新下去就可以了。

注意：应该是先求最大状态再去更新父亲节点，如果先更新再去找最大值的话，会有一部分路径是重复的。举个例子，对于2，3,6这三个点，正确的解法是先求2和当前3号节点的最大距离，然后更新2号节点，然后再轮到6号节点，这个时候2号节点里面存储的是和3号节点之间的关系，我们再去求和6号节点之间的关系，这样就不会有路径重复了。

AC代码：

 #include<bits/stdc++.h>
 using namespace std;
 # define ll long long
 const int maxn = 4e5+;
 int a[maxn],num,head[maxn],maxx;
 map<int,int>dis[maxn];
 struct node
 {
     int nex;
     int to;
 } edge[maxn];
 void init()
 {
     maxx=;
     num=;
     memset(head,-,sizeof(head));
 }
 int gcd(int n,int m)
 {
     if(n<m)
         swap(n,m);
     return n%m==?m:gcd(m,n%m);
 }
 void addedge(int fr,int to)
 {
     edge[num].nex=head[fr];
     edge[num].to=to;
     head[fr]=num++;
 }
 void dfs(int fr,int rt)
 {
     if(a[fr]>)
     {
         dis[fr][a[fr]]=;
     }
     for(int i=head[fr]; i!=-; i=edge[i].nex)
     {
         int to=edge[i].to;
         if(to==rt)continue;
             dfs(to,fr);
         for(auto t1:dis[fr])
         {
             for(auto t2:dis[to])
             {
                 if(gcd(t1.first,t2.first)!=)
                 {
                     maxx=max(maxx,t1.second+t2.second);
                 }
             }
         }
         for(auto t1:dis[to])
         {
             int tmp=gcd(a[fr],t1.first);
             if(tmp==)
                 continue;
             dis[fr][tmp]=max(dis[fr][tmp],t1.second+);
         }
     }
 }
 int main()
 {
     init();
     int n;
     scanf("%d",&n);
     int t1,t2;
     for(int i=; i<=n; i++)
     {
         scanf("%d",&a[i]);
         if(a[i]!=)
             maxx=;
     }
     for(int i=; i<=n-; i++)
     {
         scanf("%d %d",&t1,&t2);
         addedge(t1,t2);
         addedge(t2,t1);
     }
     dfs(,);
     printf("%d\n",maxx);
     return ;
 }