随手练——博弈论入门 leetcode - 486. Predict the Winner

题目链接：https://leetcode.com/problems/predict-the-winner/

1.暴力递归

当前数组左边界：i，右边界：j；

对于先发者来说，他能取到的最大值是：max(arr[i] + second(arr, i + 1, j), arr[j] + second(arr, i, j - 1));

（arr[i] + 作为后发者，在 i+1 到 j 上取得的值），（arr[j] + 作为后发者，在 i 到 j-1 上取得的值） 中大的一个。

对于后发者来说，他是被动的，他只能得到 先发者选剩下的，相对较差的那个，min(first(arr, i + 1, j), first(arr, i, j - 1));

（作为先发者，在 i+1 到 j 上取得的值），（作为先发者，在 i 到 j-1 上取得的值）中小的一个。

class Solution {
public:
    int first(vector<int>&arr,int i,int j) {
        if (i == j)return arr[i];
        , j), arr[j] + second(arr, i, j - ));
    }
    int second(vector<int>&arr, int i, int j) {
        ;
        , j), first(arr, i, j - ));
    }
    bool PredictTheWinner(vector<int>& arr) {
        , arr.size() - );
        //这个s用arr数组的sum减出来 效率更高.
        , arr.size() - );
        if (f >= s)return true;
        return false;
    }
};

2.改进暴力递归

将后发者的函数，嵌套在形参中。

第一个如果也是用求出数组的sum来减的话，两个效率应该是没什么区别的。

class Solution {
public:
    int first(vector<int>&arr, int i, int j) {
        if (i == j)return arr[i];
         == j)return max(arr[i], arr[j]);

        return max(
            arr[i] + min(first(arr, i + , j), first(arr, i + , j - )),
            arr[j] + min(first(arr, i, j - ), first(arr, i + , j - )));
    }
    bool PredictTheWinner(vector<int>& nums) {
        ;
        ; i < nums.size(); i++) {
            sum += nums[i];
        }
        , nums.size() - );
        if (sum - f <= f)return true;
        return false;
    }
};

3.动态规划

我们可以根据递归（第一个递归）的写法，改成DP，两个表都是只用得到 斜上三角部分。

先发者的表对角线是arr[i]，i = j 只有一个元素，后发者的对角线是0。

观察递归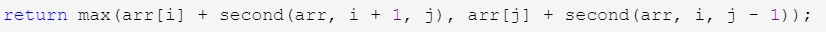  

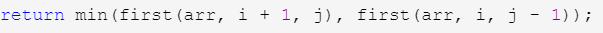
以图中为例，这个first[i][j]和second[i][j]依赖的都是橙色的四个的值。

class Solution {
public:
    ][] = {  };
    ][] = {  };
    bool PredictTheWinner(vector<int>& arr) {
        ; j < arr.size(); j++){
            f[j][j] = arr[j];
            ; i >= ; i--) {
                f[i][j] = max(arr[i] + s[i + ][j], arr[j] + s[i][j - ]);
                s[i][j] = min(f[i + ][j], f[i][j - ]);
            }
        }
        ][arr.size() - ] >= s[][arr.size() - ];
    }
};

第二个递归也是可以改成动态规划的，只用一个first数组。不过需要初始化除了对角线，还有 first[i][i+1] （0 ≤ i < arr.length）置的值。