PAT 甲级 1146 Topological Order

https://pintia.cn/problem-sets/994805342720868352/problems/994805343043829760

This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.

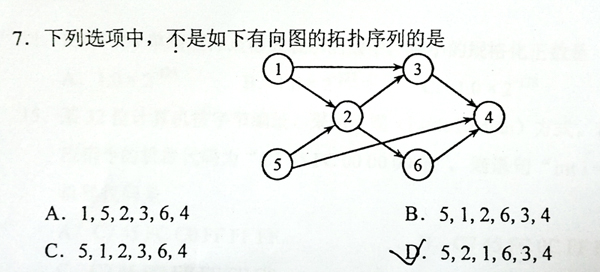
Input Specification:

Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 1,000), the number of vertices in the graph, and M (≤ 10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.

Output Specification:

Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.

Sample Input:

6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6

Sample Output:

3 4

代码：

#include <bits/stdc++.h>
using namespace std;

int N, M, K;
int topo[1010][1010];
int num[1010];
map<int, int> mp;

int main() {
    scanf("%d%d", &N, &M);
    memset(topo, 0, sizeof(topo));
    while(M --) {
        int a, b;
        scanf("%d%d", &a, &b);
        topo[a][b] = 1;
    }

    scanf("%d", &K);
    vector<int> ans;
    for(int k = 0; k < K; k ++) {
        bool flag = true;
        for(int i = 0; i < N; i ++)
            scanf("%d", &num[i]);

        for(int i = N - 1; i >= 1; i --) {
            for(int j = i - 1; j >= 0; j --) {
                if(topo[num[i]][num[j]]) {
                    flag = false;
                    break;
                }
            }
        }
        if(!flag) ans.push_back(k);
    }

    for(int i = 0; i < ans.size(); i ++)
        printf("%d%s", ans[i], i != ans.size() - 1 ? " " : "\n");
    return 0;
}

　　建立有向图 输入的每一组数据从后向前暴力如果走得通的话就是 false

FHFHFH