一、关于二叉树：

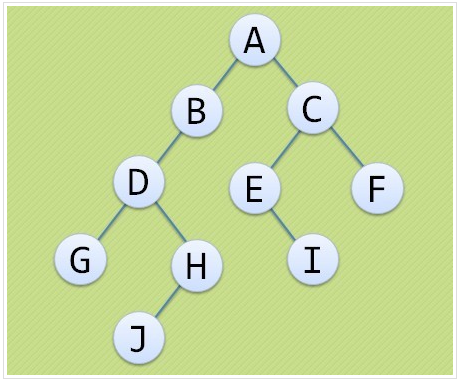
截图来自：https://segmentfault.com/a/1190000000740261

温馨提示：学习以及使用二叉树概念，心中永远有这么一个图，对于理解和接受二叉树有很大的帮助。

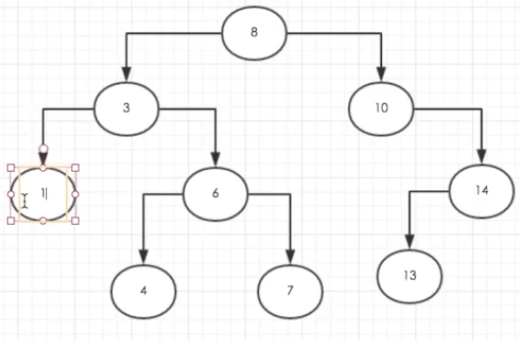
截图来自慕课：http://www.imooc.com/video/15749

　　关于二叉树概念，百度百科一大篇，百度一大堆，我也是看各种博客文章；

贴几个传送门

  1.  https://segmentfault.com/a/1190000000740261
  2.  
  3.  http://code.tutsplus.com/articles/data-structures-with-javascript-tree--cms-23393
  4.  
  5.  https://www.nczonline.net/blog/2009/06/09/computer-science-in-javascript-binary-search-tree-part-1/

二、整理的名词:

  1.  二叉树的高：二叉树的层级就是二叉树的高，有几层就是高是多少
  2.  二叉树的根：二叉树最上边没有父亲节点的第一个节点就是整个二叉树的根节点
  3.  二叉树的叶子：二叉树最下边没有孩子节点的最后一层的节点就是二叉树的叶子（就像一棵树的叶子，最末端）
  4.  二叉树特点：左边的孩子小于右边孩子的值，左边孩子值小于父亲节点的值，右边孩子的值大于父亲节点的值。【又称排序二叉树】

三、二叉树的实现

　　——用javascript生成一个二叉树：

代码：

  1.      function BinaryTree(){
  2.          var Node = function(key){
  3.              this.key = key;
  4.              this.left = null;
  5.              this.right = null;
  6.          };
  7.          var oRoot = null;
  8.          var insertNode = function(node,newNode){
  9.              if(newNode.key < node.key){
  10.                  if(node.left === null){
  11.                      node.left = newNode;
  12.                  }else{
  13.                      insertNode(node.left,newNode);
  14.                  }
  15.              }else{
  16.                  if(node.right === null){
  17.                      node.right = newNode;
  18.                  }else{
  19.                      insertNode(node.right,newNode);
  20.                  }
  21.              }
  22.          }
  23.          this.insert = function(key){
  24.              var newNode = new Node(key);
  25.              if(!(oRoot === null)){
  26.                  insertNode(oRoot,newNode)
  27.              }else{
  28.                  oRoot = newNode;
  29.              }
  30.          };
  31.      }
  32.      var nodeArr = [8,3,10,1,6,14,4,7,13];
  33.      var binaryTree = new BinaryTree();
  34.      nodeArr.forEach(function(key){
  35.          binaryTree.insert(key);
  36.      })

javascript实现二叉树结构

ps：因为是看慕课的视频跟着做的，我把代码整理下来分析了一次、以下贴分析的代码：

  1.  function BinaryTree(){//封装一个二叉树的函数
  2.          var Node = function(key){//设置一个节点函数，根节点的key是值，left表示左箭头，right表示右箭头
  3.              this.key = key;
  4.              this.left = null;
  5.              this.right = null;
  6.          };
  7.          var oRoot = null;//准备一个根节点的坑。
  8.          var insertNode = function(node,newNode){//“寻找节点位置并插入节点”函数，传参为当前节点和要加入的新节点
  9.              // 因为二叉树的数据结构特点就是根节点左边的元素值比根节点小，右边的大、。
  10.              if(newNode.key < node.key){//如果新节点比当前节点小，那就扔到左边
  11.                  if(node.left === null){//扔到左边前，先看看左边有没有空位子
  12.                      node.left = newNode;//有位子，就把这个值扔到这里
  13.                  }else{
  14.                      insertNode(node.left,newNode);//若左边没有空位子（即左边已经有了根节点，那么再次执行插入节点函数，同时比较的数变成左边这个根节点的值和新值的大小了。
  15.                  }
  16.              }else{//如果新节点比当前节点大，那就扔到右边
  17.                  if(node.right === null){//扔到右边前，看看有没有地方
  18.                      node.right = newNode;//有地方直接扔进去
  19.                  }else{
  20.                      insertNode(node.right,newNode);//没地方，那就重新遍历，遍历换成比较右边占着茅坑的这个值和要放进来的新值的大小
  21.                  }
  22.              }
  23.          }
  24.          this.insert = function(key){//"插入根节点"函数
  25.              var newNode = new Node(key);//传进来的key值，作为新值
  26.              if(!(oRoot === null)){//如果第一层的根节点不为空
  27.                  insertNode(oRoot,newNode);//往根节点的下一层插入去,执行“寻找节点位置并插入节点”函数，根据二叉树的数据结构特点和原则【根节点左边的元素值比根节点小，右边的元素值比根节点大】判断性的寻找正确的位置并插入
  28.              }else{
  29.                  oRoot = newNode;//根节点为空，就是整个树还为空，那就让这个值作为根节点占住根节点的位、
  30.              }
  31.          };
  32.      }
  33.  var nodeArr = [8,3,10,1,6,14,4,7,13];//要遍历的数组
  34.  var binaryTree = new BinaryTree();//把整个自定义的二叉树函数送给这个变量指针
  35.  nodeArr.forEach(function(key){//遍历数组，并传入要遍历的值
  36.      binaryTree.insert(key);//执行二叉树函数的"插入根节点"函数，开始插入函数。
  37.  })

四、二叉树的遍历

　　中序遍历

　　　　顺序(左中右)：先访问当前节点的左子树直到左子树为空，再打印当前值，最后访问当前节点的右子树

　　　　作用：用于排序一个数组，从小到大升序排列。

　　前序遍历

　　　　顺序(中左右)：先访问并打印当前节点的值，然后访问当前节点的左子树，最后访问当前节点的右子树

　　　　作用：复制一个已有的二叉树结构，性能是最高的。比重新创造一个新的二叉树的效率高十倍多。

　　后序遍历

　　　　顺序(左右中)：先访问当前节点的左子树，然后访问当前节点的右子树，最后访问并打印当前节点值

　　　　作用：用于操作系统和文件系统的遍历上。

1、中序遍历

源码：

  1.   // 中序遍历函数封装
  2.  var inOrderTraverseNode = function(node,callback){
  3.        if(node !== null){
  4.           inOrderTraverseNode(node.left,callback);//这种在函数身体里边再调用函数自身的方法真的要注意使用！
  5.           callback(node.key);
  6.           inOrderTraverseNode(node.right,callback);
  7.       }
  8.   }
  9.   // 增加遍历的api接口
  10.   this.inOrderTraverse = function(callback){
  11.       inOrderTraverseNode(oRoot,callback);
  12.  }

中序遍历 Code

中序遍历源码解析

  1. <script>
  2. //在原来二叉树函数的基础上继续补充
  3. 	function BinaryTree(){
  4. 		// 中序遍历函数封装
  5. 		var inOrderTraverseNode = function(node,callback){//接收根节点的值和回调函数
  6. 			if(node !== null){//首先判断,二叉树的当前节点里边有没有内容
  7. 				inOrderTraverseNode(node.left,callback);//如果该节点左边有分节点（左边有孩子）那么在左孩子的位置基础上，再次调用中序遍历函数，并把当前左孩子的值传给函数。直到找不到左孩子时这个才会停止，函数会一层一层的嵌套。那么，直到最后一层的叶子级别的左孩子，就不会继续调用这个函数了，也就是会遍历到树的最左下角的那个节点了。
  8. 				//这种在函数身体里边再调用函数自身的方法真的要注意使用！
  9. 				callback(node.key);//输出当前的值
  10. 				inOrderTraverseNode(node.right,callback);//再看看这个节点上有没有右节点，如果有，就站在右节点的位置上，再次执行这个函数，那么下次遍历的就会是这个右节点的左孩子是否存在了。
  11. 			}
  12. 		}
  13. 		// 增加遍历的api接口
  14. 		this.inOrderTraverse = function(callback){//后期调用
  15. 			inOrderTraverseNode(oRoot,callback);//接口内，调用中序遍历函数，并且传入当前的根节点的值和回调函数。传oRoot是因为要从根节点开始。
  16. 		}
  17. 	};
  18.  
  19. 	var callback = function(key){// 增加遍历的自定义效果的回调函数
  20. 		console.log(key);//每次遍历后输出当前的遍历值。
  21. 	};
  22.  
  23. 	binaryTree.inOrderTraverse(callback);// 调用封装好的遍历方法api，以实现遍历二叉树的目标。
  24. </script>

2、前序遍历

（ps：由于和中序遍历的结构基本一致，只是遍历的顺序稍有改变，不再做具体的分析。）

  1.  <!DOCTYPE html>
  2.  <html lang="en">
  3.  <head>
  4.      <meta charset="UTF-8">
  5.      <title>二叉树的前序遍历</title>
  6.      <meta name="author" content="xing.org1^">
  7.      <meta name="description" content="二叉树的遍历之前序遍历法。">
  8.      <meta name="description" content="中序遍历的作用是数组从小到大按照升序排列，前序遍历的作用是用来复制一个已有的二叉树结构，利用性能是最高的。用前序遍历复制的二叉树，效率要比重新构造一个二叉树高得多">
  9.  </head>
  10.  <body>
  11.      <h3>前序遍历的特点就是遍历次序的不一样，先打印当前节点，然后访问当前节点的左子树，再然后打印当前节点的右子树</h3>
  12.      <h4>用前序遍历拷贝一个二叉树，只需要依次遍历所有的子节点就好了。</h4>
  13.      <script>
  14.          var arr = [1,8,34,67,23,2];
  15.          var newArr = [];
  16.          var binaryTree = new BinaryTree();
  17.          console.log("原数组为："+arr)
  18.          var callBack = function(key){
  19.              console.log("复制——"+key);
  20.              newArr.push(key);
  21.          }
  22.          arr.forEach(function(key){
  23.              binaryTree.startCreateBinary(key);
  24.          });
  25.          binaryTree.startTraverseBinary(callBack);
  26.          console.log("最后复制出数组为："+newArr);
  27.  
  28.          // 二叉树
  29.          function BinaryTree(){
  30.              var Node = function(key){
  31.                  this.key = key;
  32.                  this.left = null;
  33.                  this.right = null;
  34.              };
  35.              var oRoot = null;
  36.              this.startCreateBinary = function(key){
  37.                  var newNode = new Node(key);
  38.                  if(oRoot){
  39.                      createBinary(oRoot,newNode)
  40.                  }else{
  41.                      oRoot = newNode;
  42.                  }
  43.              }
  44.  
  45.              var createBinary = function(node,newNode){
  46.                  if(node.key > newNode.key){
  47.                      // 这里欠缺思考：如果当前值和根节点的值相等呢？放哪边？
  48.                      if(node.left){
  49.                          createBinary(node.left,newNode);
  50.                      }else{
  51.                          node.left = newNode;
  52.                      }
  53.                  }else{
  54.                      if(node.right){
  55.                          createBinary(node.right,newNode);
  56.                      }else{
  57.                          node.right = newNode;
  58.                      }
  59.                  }
  60.              };
  61.  
  62.              this.startTraverseBinary = function(callback){
  63.                      traverseBinary(oRoot,callback);
  64.              };
  65.              // 前序遍历
  66.              var traverseBinary = function(node,callback){
  67.                  if(node){
  68.                      callback(node.key);
  69.                      traverseBinary(node.left,callback);
  70.                      traverseBinary(node.right,callback);
  71.                  }
  72.              };
  73.          }
  74.      </script>
  75.  </body>
  76.  </html>

二叉树结构生成和前序遍历

3、后序遍历

  1.  <!DOCTYPE html>
  2.  <html lang="en">
  3.  <head>
  4.      <meta charset="UTF-8">
  5.      <meta name="author" content="xing.org1^">
  6.      <meta name="description" content="二叉树的遍历之后序遍历法。">
  7.      <title>后序遍历</title>
  8.  </head>
  9.  <body>
  10.      <h3>访问顺序：先访问左子树，在访问右子树，最后访问当前节点的值</h3>
  11.      <h3>作用：应用到操作系统、文件系统的遍历之中</h3>
  12.      <h3>由下边代码可以看到，他把数组给反过来了，反着输出了一遍</h3>
  13.      <script>
  14.      var arr = [23,1,82,845,9,25,0];
  15.      var newArr = [];
  16.      var binaryTree = new BinaryTree();
  17.      var callBack = function(key){
  18.          console.log(key);
  19.          newArr.push(key);
  20.      }
  21.      arr.forEach(function(key){
  22.          binaryTree.startCreateBinary(key);
  23.      });
  24.      binaryTree.startTraveralBinary(callBack);
  25.      console.log(newArr);
  26.      // 二叉树
  27.          function BinaryTree(){
  28.              var Node = function(key){
  29.                  this.key = key;
  30.                  this.left = null;
  31.                  this.right = null;
  32.              };
  33.              // 创建
  34.              var oRoot = null;
  35.              this.startCreateBinary = function(key){
  36.                  var newNode = new Node(key);
  37.                  if(oRoot){
  38.                      createBinary(oRoot,newNode);
  39.                  }else{
  40.                      oRoot = newNode;
  41.                  }
  42.              }
  43.              var createBinary = function(node,newNode){
  44.                  if(node.key > newNode.key){//这里特别注意，比较的是值的大小，不是两个函数，一定要加.key属性！！！
  45.                      if(node.left){
  46.                          createBinary(node.left,newNode);
  47.                      }else{
  48.                          node.left = newNode;
  49.                      }
  50.                  }else{
  51.                      if(node.right){
  52.                          createBinary(node.right,newNode);
  53.                      }else{
  54.                          node.right = newNode;
  55.                      }
  56.                  }
  57.              };
  58.  
  59.              // 遍历
  60.              this.startTraveralBinary = function(callback){
  61.                  traveralBinary(oRoot,callback);
  62.              }
  63.              var traveralBinary = function(node,callback){
  64.                  if(node){
  65.                      traveralBinary(node.left,callback);
  66.                      traveralBinary(node.right,callback);
  67.                      callback(node.key);
  68.                  }else{
  69.                      console.log("没有结构，不用遍历！");
  70.                  }
  71.              };
  72.          };
  73.      </script>
  74.  </body>
  75.  </html>

二叉树结构生成和后序遍历

二叉树的结构生成和中序遍历——示例解析：

中序遍历二叉树生成排序数组

  1. <!DOCTYPE html>
  2. <html lang="en">
  3. <head>
  4. 	<meta charset="UTF-8">
  5. 	<meta name="author" content="郭菊锋">
  6. 	<meta name="description" content="二叉树中序遍历分析">
  7. 	<title>中序遍历二叉树生成排序数组</title>
  8. </head>
  9. <body>
  10. 	<script>
  11. 		function tree(){//封装一个二叉树的函数
  12. 			// 创建一个空的根节点，根节点的值是参数key，创建left表示左箭头，创建right表示右箭头
  13. 			var oNode = function(key){
  14. 				this.key = key;
  15. 				this.left = null;
  16. 				this.right = null;
  17. 			}
  18. 			// 开始构造二叉树 api
  19. 			// 创建并确定第一层的根节点
  20. 			var oRoot = null;//空的根节点，准备一个根节点的坑。
  21. 			this.startTree = function(key){//"插入根节点"函数，设置一个开始的接口方法
  22.  
  23. 				var newNode = new oNode(key);//每次执行都创建一个新的节点，传进来的key值作为新值。
  24. 				if (!(oRoot === null)) {//如果第一层的根节点不为空
  25. 					binaryTree.createTree(oRoot,newNode)
  26. 					//第一个值以后的值,把他们当做新节点给了根的孩子们，让他们依次当爸爸妈妈。
  27. 					//往根节点的下一层插入去,执行“寻找节点位置并插入节点”函数，根据二叉树的数据结构特点和原则【根节点左边的元素值比根节点小，右边的元素值比根节点大】判断性的寻找正确的位置并插入
  28. 				} else {
  29. 					//else,根节点为空，就是整个树还为空，那就让这个值作为根节点占住根节点的位、
  30. 					oRoot = newNode;//把第一次创建的节点给了根。
  31. 				}
  32. 			}
  33. 			// 创造二叉树 api
  34. 			// 在子层依次按规律寻找位置存放新节点
  35. 			this.createTree = function(node,newNode){//设置一个创造的方法
  36. 				//“寻找节点位置并插入节点”函数，参数为当前节点和要加入的新节点
  37. 				// 因为二叉树的数据结构特点就是根节点左边的元素值比根节点小，右边的大、。
  38. 				console.log(newNode)
  39. 				if(newNode.key < node.key){//后边的新值比当前值小的话，放左边，否则放右边
  40. 				//如果新节点比当前节点小，那就扔到左边.特别注意这里比较的是节点的值，如果你错误地比较节点的话，将永远都是走else流程的。
  41. 					if(node.left === null){//扔到左边前，先看看左边有没有空位子，没位置也放不下，没位置就在左边这里继续和左边的值判断，如果小于左边的值，放左边值的孩子层的左边，反之大就放右边
  42. 						node.left = newNode;//左边有位子（即为空值），就把这个值扔到这里
  43. 					}else{
  44. 						binaryTree.createTree(node.left,newNode);//若左边没有空位子（即左边已经有了根节点，那么再次执行插入节点函数，同时比较的数变成左边这个根节点的值和新值的大小了。也就是站在node.left的基础上，以node.left作为新的根节点去查找他的下一级进行再次判断，看看newNode是放到他下边的左边还是右边
  45. 						//注意上边如果是var声明的函数，则不用binaryTree这么调，如果是通过this.加给binaryTree的方法，那么需要通过binaryTree来调用这个接口。
  46. 					}
  47. 					// 接下来同左边了
  48. 				}else{//如果新节点比当前节点大，那就扔到右边
  49. 					if(node.right === null){//扔到右边前，看看有没有地方
  50. 						node.right = newNode;//有地方直接扔进去
  51. 					}else{
  52. 						binaryTree.createTree(node.right,newNode);//没地方，那就重新遍历，遍历换成比较右边占着茅坑的这个值和要放进来的新值的大小
  53. 					}
  54. 				}
  55. 			};
  56. 			// 遍历二叉树的接口 api
  57. 			this.startLDR = function(callback){
  58. 				centerTraverse(oRoot,callback);//接口内，调用中序遍历函数，并且第一次调用，传入当前的根节点的值和回调函数。传oRoot是因为要从根节点开始。
  59. 			}
  60. 			// 遍历二叉树——中序遍历函数
  61. 			//中序遍历的顺序就是左根右，所以先node.left、再node.key、最后node.right
  62. 			var centerTraverse = function(node,callback){//用var声明（所以后期调用就不用父亲的权限了，区别于this声明）一个中序遍历函数，接收参数为节点的值和回调函数
  63. 				if(!(node === null)){//首先判断,二叉树的当前节点里边有没有内容
  64. 					centerTraverse(node.left,callback);//这种在函数身体里边再调用函数自身的方法真的要注意使用！
  65. 					//如果该节点左边有分节点（左边有孩子）那么在左孩子的位置基础上，再次调用中序遍历函数，并把当前左孩子的值传给函数。直到找不到左孩子时这个才会停止，函数会一层一层的嵌套。那么，直到最后一层的叶子级别的左孩子，就不会继续调用这个函数了，也就是会遍历到树的最左下角的那个节点了。
  66. 					callback(node.key);//得到当前遍历的值然后当参数传给callback函数，然后。看自己的需求，遍历到当前值时自己需要什么操作就写在callback里。我这里只用了console.log输出当前的值,和push把当前值放进新数组里以求得到顺序遍历后的新排序函数。
  67. 					centerTraverse(node.right,callback);//再看看这个节点上有没有右节点，如果有，就站在右节点的位置上，再次执行这个函数，那么下次遍历的就会是这个右节点的左孩子是否存在了。
  68. 				}
  69. 			}
  70. 		};
  71. 		// 执行二叉树，整理数组
  72. 		var arr = [8,3,16,12,18,39,20,23];//准备一个数组
  73. 		var binaryTree = new tree();//把封装好的二叉树函数给一个变量指针
  74. 		arr.forEach(function(key){//利用forEach循环函数，依次将数组中的值放在二叉树中
  75. 			binaryTree.startTree(key);
  76. 		})
  77. 		var aT = [];
  78. 		var callback = function(key){//回调函数，用于二叉树执行遍历后，接收返回的值。
  79. 			console.log(key);//依次输出值用于调试
  80. 			aT.push(key);//利用push把每次输出的值放到空数组中，生成一个新的排序数组
  81. 		}
  82. 		binaryTree.startLDR(callback);//调用遍历函数接口，执行遍历二叉树的命令
  83. 		console.log(aT);
  84. 	</script>
  85. </body>
  86. </html>

四、二叉树的节点查找：

1.查找最小值：

　　其实就是一直遍历，从根节点开始，找当前节点的左孩子，直到某个节点没有左孩子了，那么这个节点就是整个二叉树的最小值了

（因为左孩子里的值比节点的值小，右节点的比当前节点的大。这是一个固定规律。）

  1.  if(node){
  2.      if(node.left){
  3.          node = node.left;
  4.          return searchMinBinary(node);
  5.      }else{
  6.          return node.key;
  7.      }
  8.  }
  9.  return null;

if方法

  1.  if(node){
  2.      while(node && node.left !== null){
  3.          node = node.left;
  4.      }
  5.      return node.key;
  6.  }
  7.  return null

while方法

2.查找最大值：

　　同样的，从根节点一直向右找，找当前节点的右孩子，直到找到某个节点他没有右节点的时候，那么这个节点就是整个二叉树的最大值。

  1.  if(node){
  2.      while(node && node.right !== null){
  3.          node = node.right;
  4.      }
  5.      return node.key;
  6.  }
  7.  return null;

while方法

3.查找对应值：

　　从根节点开始，先判断当前节点与给定节点的值是否一样，一样就是这个节点的值。

　　不一样就判断给定的值和当前节点的值的大小，

　　若给定值小于当前节点的值就向左（进入当前节点的左子树进行比对）查找，

　　若大于当前节点的值就向右（进入当前节点的右子树进行比较）查找。

　　若最终找不到给定的值，就是没有这个值，查找失败。

  1.  if(node){
  2.      if(node.key == newNode){
  3.          return node.key;
  4.      }else if(node.key > newNode){
  5.          node = node.left;
  6.          return searchBinary(node,newNode);
  7.      }else{
  8.          node = node.right;
  9.          return searchBinary(node,newNode);
  10.      }
  11.  }
  12.  console.log("没有结果");

if判断查找对应值

三种查找情况的示例代码及分析：

  1.  <!DOCTYPE html>
  2.  <html lang="en">
  3.  <head>
  4.      <meta charset="UTF-8">
  5.      <meta name="author" content="xing.org1^">
  6.      <meta name="description" content="二叉树的节点查找">
  7.      <title>二叉树的节点查找</title>
  8.  </head>
  9.  <body>
  10.      <h4>查找节点的理念就是：看这个节点是不是在二叉树当中。</h4>
  11.      <h4>应用：广泛</h4>
  12.      <h4>方法分为三种：</h4>
  13.      <ol>
  14.          <li>查找二叉树节点的最小值：其实就是一直遍历，从根节点开始，找当前节点的左孩子，直到某个节点没有左孩子了，那么这个节点就是整个二叉树的最小值了（因为左孩子里的值比节点的值小，右节点的比当前节点的大。这是一个固定规律。）</li>
  15.          <li>查找二叉树节点的最大值：同样的，从根节点一直向右找，找当前节点的右孩子，直到找到某个节点他没有右节点的时候，那么这个节点就是整个二叉树的最大值。</li>
  16.          <li>二叉树节点中查找给定的相应节点的值：从根节点开始，先判断当前节点与给定节点的值是否一样，一样就是，不一样就判断给定的值和当前节点的值的大小，若给定值小于当前节点的值就向左（进入当前节点的左子树进行比对）查找,若大于当前节点的值就向右（进入当前节点的右子树进行比较）查找。若最终找不到给定的值，就是没有这个值，查找失败。</li>
  17.      </ol>
  18.      <script>
  19.          var    arr = [3416,33,423,212,12];
  20.          var binaryTree = new BinaryTree();
  21.          arr.forEach(function(key){
  22.              binaryTree.startCreateBinary(key);
  23.          });
  24.          // 调用接口，查找二叉树的最小值。
  25.          var minArr = binaryTree.startSearchBinary("min");
  26.          var maxArr = binaryTree.startSearchBinary("max");
  27.          console.log("最小值为："+minArr);
  28.          console.log("最大值为："+maxArr)
  29.          var searchNum = binaryTree.startSearchBinaryNum(1);
  30.          console.log(searchNum);
  31.          // 二叉树
  32.          function BinaryTree(){
  33.              var Node = function(key){
  34.                  this.key = key;
  35.                  this.left = null;
  36.                  this.right = null;
  37.              };
  38.              var oRoot = null;
  39.              this.startCreateBinary = function(key){
  40.                  var newNode = new Node(key);
  41.                  if(oRoot){
  42.                      createBinary(oRoot,newNode);
  43.                  }else{
  44.                      oRoot = newNode;
  45.                  }
  46.              };
  47.              var createBinary = function(node,newNode){
  48.                  if(node.key > newNode.key){//这里是比较两个值的大小，在这里栽坑十几次了！！！
  49.                      if(node.left){
  50.                          createBinary(node.left,newNode);
  51.                      }else{
  52.                          node.left = newNode;
  53.                      }
  54.                  }else{
  55.                      if(node.right){
  56.                          createBinary(node.right,newNode);
  57.                      }else{
  58.                          node.right = newNode;
  59.                      }
  60.                  }
  61.              };
  62.              // 查找并返回二叉树节点(最大值/最小值)
  63.              this.startSearchBinary = function(type){
  64.                  if(type === "min"){
  65.                      return searchMinBinary(oRoot);
  66.                  }else{
  67.                      return searchMaxBinary(oRoot);
  68.                  }
  69.              };
  70.              var searchMinBinary = function(node){
  71.                  if(node){
  72.                      // 这里判断是否有左子树的方法除了while还可以用if方法！
  73.                      if(node.left){
  74.                          // 这里，当本节点有左子节点时，应该把左子树当做新的根节点重新查找
  75.                          node = node.left;//函数内部，数值身份的转换。
  76.                          return searchMinBinary(node);//这里依然递归调用的话，会导致虽然找到最小的1，但是找最小值的函数是嵌套在父元素的，等找完最小值后还会执行父节点剩下的函数，也就是后边return 2那里。所以最后返回的都将是2。所以解决方法是这里return出去，让他停止继续递归。霍哈哈哈，所以我自己写的if判断的写法是有用的。
  77.                      }else{
  78.                          // 查找左子树一直找不到的时候应该怎么办？返回当前值啊！就是node的key值啊！
  79.                          return node.key;
  80.                      }
  81.                  }
  82.                      return null;
  83.  
  84.                  // while方法
  85.                  // if(node){
  86.                  //     while(node && node.left !== null){
  87.                  //         node = node.left;
  88.                  //     }
  89.                  //     return node.key;
  90.                  // }
  91.                  // return null//连二叉树都是空的话，那就直接返回空。
  92.              };
  93.              var searchMaxBinary = function(node){
  94.                  if(node){
  95.                      while(node && node.right !== null){
  96.                          node = node.right;
  97.                      }
  98.                      return node.key;
  99.                  }
  100.                  return null;
  101.              };
  102.              // 查找某个特定的值
  103.              this.startSearchBinaryNum = function(key){
  104.                  return searchBinary(oRoot,key)
  105.              }
  106.              var searchBinary = function(node,newNode){
  107.                  if(node){
  108.                      if(node.key == newNode){
  109.                          return node.key;
  110.                      }else if(node.key > newNode){
  111.                          node = node.left;
  112.                          // searchBinary(node,newNode);//这种写法导致我每次都是嵌套遍历，然后最后结果都是console.log("没有结果");后来发现，这里也应该有return，不然即使找到了相应的值，但是语句还是会继续执行所以导致最后都是不正确的值！
  113.                          return searchBinary(node,newNode);
  114.                      }else{
  115.                          node = node.right;
  116.                          return searchBinary(node,newNode);
  117.                      }
  118.                  }
  119.                  console.log("没有结果");
  120.              };
  121.          }
  122.      </script>
  123.  </body>
  124.  </html>

二叉树的节点查找示例分析

五、二叉树的节点删除：

　1.删除叶子节点 --> 叶子节点的特点：左右子节点都为空；

　　方法：通过判断找到这个叶子节点（特点是：node.left === null && node.right === null）,然后把这个节点改成node = null；就是删除了

  1. // 删除二叉树的叶子节点
  2. this.startRemoveNode = function(key){//创建一个删除的接口，传进一个要删除的值
  3. 	oRoot = removeLeafNode(oRoot,key);//调用删除方法，传入两个值，第一次要比较的根节点和传进来的值。
  4. };
  5. // 删除叶子节点方法
  6. var removeLeafNode = function(node,key){
  7. 	if(node === null){//判断整个二叉树是否为空
  8. 		return null;
  9. 	}//
  10. 	if(key < node.key){//判断要删除的值与当前节点的值是否相等
  11. 		node.left = removeNode(node.left,key);//如果不相等，那就站在node.left这个节点上，继续调用一遍删除节点的函数
  12. 		return node;//如果他的子节点刚好是要删除的那个，删完回来后返回node
  13. 	}else if(key > node.key){//同理node.left
  14. 		node.right = removeNode(node.right,key);
  15. 		return node;
  16. 	}else{//当前节点的值刚好等于要删除的值，
  17. 		if(node.left === null && node.right === null){//并且符合叶子节点的特点：左右子节点都为空；
  18. 			node = null;//把当前节点设为空表示删除这个节点了。
  19. 			return node;
  20. 		}
  21. 	}
  22. };

　2.删除中间节点（即有子节点的节点）

　　1）如果左右孩子都是空（即叶子节点）：直接删除 (node=null) 即可

　　代码见上边“删除叶子节点”。

　　2）左孩子为空：没有左孩子的情况，删了以后让父节点直接指向该节点的右孩子；

　　

  1. if(node.left === null){//如果中间节点只有右孩子
  2. 	node = node.right;
  3. 	return node;
  4. }

　

　　3）右孩子为空：没有右孩子的情况，删了以后让父节点直接指向该节点的左孩子；

  1. if(node.right === null){//如果中间节点只有左孩子
  2. 	node = node.left;// 即右子节点为空，则将本节点等于他的左节点
  3. 	return node;
  4. }

　　

　　4）如果左右孩子都存在：左右孩子都有，删除本节点后，找到右子节点里边，最左边的子节点（也就是右孩子下边最小的值，最底层的最小的左子孙子）；让这个左子孩子的值等于当前值。再从新找到这个值删掉。（也就相当于把当前节点右孩子中最左边最小的叶子元素移动到并替换了当前节点）；

  1. // 找到最小值节点
  2. var findMinNode = function(node){
  3. 	if(node) {
  4. 		while(node && node.left !== null){
  5. 			node = node.left;
  6. 		}
  7. 		return node;
  8. 	}
  9. 	return null;
  10. }
  11. // 找到这个中间节点的右孩子的最小的左孩子，然后把值复制下来，再把这个孩子删除掉（相当于把这个孩纸移动过来了)
  12. var aux = findMinNode(node.right);
  13. node.key = aux.key;
  14. node.right = removeNode(node.right,aux.key);

　　

 删除节点的方法汇总：

  1. <script>
  2. 	var arr = [23,15,54,1,6213,17];
  3. 	console.log(arr);
  4. 	var binaryTree = new BinaryTree();
  5. 	arr.forEach(function(key){
  6. 		binaryTree.startCreateBinary(key);
  7. 	});
  8. 	binaryTree.startRemoveNode(1);
  9. 	console.log(arr);
  10. 	function BinaryTree(){
  11. 		var Node = function(key){
  12. 			this.key = key;
  13. 			this.left = null;
  14. 			this.right = null;
  15. 		}
  16. 		var oRoot = null;
  17. 		this.startCreateBinary = function(key){
  18. 			var newNode = new Node(key);
  19. 			if(oRoot){
  20. 				createBinary(oRoot,newNode);
  21. 			}else{
  22. 				oRoot = newNode;
  23. 			}
  24. 		};
  25. 		var createBinary = function(node,newNode){
  26. 			if(node.key > newNode.key){
  27. 				if(node.left){
  28. 					createBinary(node.left,newNode);
  29. 				}else{
  30. 					node.left = newNode;
  31. 				}
  32. 			}else{
  33. 				if(node.right){
  34. 					createBinary(node.right,newNode);
  35. 				}else{
  36. 					node.right = newNode;
  37. 				}
  38. 			}
  39. 		};
  40. 		// 找到最小值节点
  41. 		var findMinNode = function(node){
  42. 			if(node) {
  43. 				while(node && node.left !== null){
  44. 					node = node.left;
  45. 				}
  46. 				return node;
  47. 			}
  48. 			return null;
  49. 		}
  50. 		// 删除二叉树的叶子节点
  51. 		this.startRemoveNode = function(removeKey){//创建一个删除的接口，传进一个要删除的值
  52. 			oRoot = removeNode(oRoot,removeKey);//调用删除方法，传入两个值，第一次要比较的根节点和传进来的值。
  53. 		};
  54. 		// 删除叶子节点方法+删除中间节点的方法
  55. 		var removeNode = function(node,removeKey){
  56. 			if(node === null){//判断整个二叉树是否为空
  57. 				return null;
  58. 			}//
  59. 			if(removeKey < node.key){//判断要删除的值与当前节点的值是否相等
  60. 				node.left = removeNode(node.left,removeKey);//如果不相等，那就站在node.left这个节点上，继续调用一遍删除节点的函数
  61. 				return node;//如果他的子节点刚好是要删除的那个，删完回来后返回node
  62. 			}else if(removeKey > node.key){//同理node.left
  63. 				node.right = removeNode(node.right,removeKey);
  64. 				return node;
  65. 			}else{//当前节点的值刚好等于要删除的值，
  66. 				// 如果左右两个节点都没有（就是叶子节点）
  67. 				if(node.left === null && node.right === null){//并且符合叶子节点的特点：左右子节点都为空；
  68. 					node = null;//把当前节点设为空表示删除这个节点了。
  69. 					return node;
  70. 				};
  71.  
  72. 				//删除中间节点（即有子节点的节点)
  73. 					// 如果左子节点为空，则将本节点等于他的右节点
  74. 				if(node.left === null){//如果中间节点只有右孩子
  75. 					node = node.right;
  76. 					return node;
  77. 				}else if(node.right === null){//如果中间节点只有左孩子
  78. 					node = node.left;// 即右子节点为空，则将本节点等于他的左节点
  79. 					return node;
  80. 				}
  81. 					// 如果左右两个节点都有
  82. 				// 找到这个中间节点的右孩子的最小的左孩子，然后把值复制下来，再把这个孩子删除掉（相当于把这个孩纸移动过来了)
  83. 				var aux = findMinNode(node.right);
  84. 				node.key = aux.key;
  85. 				node.right = removeNode(node.right,aux.key);
  86. 			}
  87. 		};
  88. 	}
  89. </script>

　　

~完

JS - 二叉树算法实现与遍历 (更新中...)的更多相关文章

  1. leetcode 257. 二叉树的所有路径 包含（二叉树的先序遍历、中序遍历、后序遍历）

    给定一个二叉树,返回所有从根节点到叶子节点的路径. 说明: 叶子节点是指没有子节点的节点. 示例: 输入: 1 / \2 3 \ 5 输出: ["1->2->5", & ...

  2. 百度前端学院js课堂作业合集+分析(更新中...)

    第一课:简陋的登录框 <!DOCTYPE html> <html lang="en"> <head> <meta charset=&quo ...

  3. JS基础知识再整理..........不断更新中

    1.JS的五种基本数据类型:字符串.数值.布尔.null.underfined. 2.在JS中,字符串.数值.布尔三种数据类型,有其属性和方法: 3.字符串的三种常用方法[.indexof()..su ...

  4. js 二叉树算法

    //生成二叉树 function binarySearchTree() { let Node = function(key) { this.key = key; this.left = null; t ...

  5. 常用JS、jquery 命令（不断更新中）

    设置用户粘贴板中的文本信息:window.clipboardData.setData('Text', location.href); 获取用户粘贴板中的文本信息: window.clipboardDa ...

  6. L2-006 树的遍历 （25 分) （根据后序遍历与中序遍历建二叉树）

    题目链接:https://pintia.cn/problem-sets/994805046380707840/problems/994805069361299456 L2-006 树的遍历 (25 分 ...

  7. PTA L2-006 树的遍历-二叉树的后序遍历+中序遍历，输出层序遍历 团体程序设计天梯赛-练习集

    L2-006 树的遍历(25 分)   给定一棵二叉树的后序遍历和中序遍历,请你输出其层序遍历的序列.这里假设键值都是互不相等的正整数. 输入格式: 输入第一行给出一个正整数N(≤),是二叉树中结点的 ...

  8. [leetcode]_根据二叉树的先序遍历(后序遍历) + 中序遍历 重建二叉树

    题目1:Construct Binary Tree from Preorder and Inorder Traversal 给定一棵二叉树的先序遍历和中序遍历,求重建二叉树. 思路: 1.先序遍历的第 ...

  9. js坑爹笔试题目汇总（持续更新中）

    把你的面试官问倒,你就是一个合格的面试者了,以下总结一些易错的js笔试题目,会持续更新中.欢迎关注 1,考察this var length = 10 function fn(){ alert(this ...

随机推荐

  1. 每天一个linux命令:Linux 目录结构

    对于每一个Linux学习者来说,了解Linux文件系统的目录结构,是学好Linux的至关重要的一步.,深入了解linux文件目录结构的标准和每个目录的详细功能,对于我们用好linux系统至关只要,下面 ...

  2. SSL 证书服务推荐

    最近要用到ssl.故做了一些搜索 1.Let's Encrypt:免费,快捷,支持多域名(不是通配符),三条命令即时签署+导出证书.缺点是暂时只有三个月有效期,到期需续签. 2.StartSSL免费D ...

  3. maven2中snapshot快照库和release发布库的应用

    在之前的文章中介绍了maven2中snapshot快照库和release发布库的区别和作用,我今天这里要介绍的是如何在项目中应用snapshot和release库,应用snapshot和release ...

  4. Maven最佳实践-distributionManagement

    分发构件至远程仓库 mvn install 会将项目生成的构件安装到本地Maven仓库,mvn deploy 用来将项目生成的构件分发到远程Maven仓库.本地Maven仓库的构件只能供当前用户使用, ...

  5. 安卓开发笔记——打造万能适配器(Adapter)

    为什么要打造万能适配器? 在安卓开发中,用到ListView和GridView的地方实在是太多了,系统默认给我们提供的适配器(ArrayAdapter,SimpleAdapter)经常不能满足我们的需 ...

  6. Android 代码自动提示功能

    Eclipse for android 实现代码自动提示智能提示功能,介绍 Eclipse for android 编辑器中实现两种主要文件 java 与 xml 代码自动提示功能,解决 eclips ...

  7. CStringArray error C2248: 'CObject::CObject' : cannot access private member declared in class

    在开发中将一个字符串分割,并将子字符串保存在CStringArray中,专门写了一个函数,如下: SplitStringToCString(CString str, TCHAR tszSplit, C ...

  8. kettle教程二

    转载:http://www.cnblogs.com/limengqiang/archive/2013/01/16/KettleApply2.html 1.应用场景 这里简单概括一下几种具体的应用场景, ...

  9. v9定时发布的简单实现方法[支持静态生成]

    将以下代码放到 api/count.php 文件最后 的 ?>之前 //add 定时发布审核功能 $modelid = $modelid ? $modelid : intval($_GET['m ...

  10. 用VS2012不能打开VS2010的项目

    应该是装过sql2012或者sql2008,自带的那个visual studio,你可以直接在外面打开VS2012,然后用里面的文件去打开项目.而不要直接双击那个解决方案的文件.