[備註] 安裝與整合 xUnit 測試框架＠VS2012

開發環境：Visual Studio 2012, Update 1 (必須)。

說明：VS2012 已整合各測試框架的 Test Runner，包括 NUnit, xUnit 等。藉由標準的介面，可讓各類測試框架於 VS2012 內的 Test Explorer 歸納測試方法 (methods)，並執行測試、瀏覽測試結果。

xUnit 可說是繼老牌 NUnit 的後起之秀。關於兩者之間的比較，可參考－xuint和其他的單元測試框架的比較。個人尤為欣賞 xUnit 的 DDT (Data Driven Test)的機制－Theory，可參考這一篇－xUnit Theory, the Data Driven Unit Test。

xUnit Theory 可讓測試方法具有參數 (parameters)，而能接收多個資料來源 (InlineData, PropertyData, ClassData, ExcelData, OleDB/Sql ServerData)的資料輸入，讓測試機制更能充分利用測試數據。一個 Theory 可參考如下的寫法。

 1: [Theory]
 2: [InlineData(1, 2, 3)]
 3: [InlineData(3, 4, 7)]
 4: [InlineData(30, 10, 40)]
 5: public void Add_AddDataValues_ReturnsExpectedResult(int first, int second, int expected)
 6: {
 7:     var actualResult = Calculator.Add(first, second);
 8:
 9:     Assert.Equal(expected, actualResult);
10: }

安裝：兩個 xUnit 套件是必要安裝的 (全於 VS2012 內安裝)。

1. xUnit.net runner for Visual Studio 2012 extension。
2. 利用 NuGet 安裝 xUnit.NET。

o xUnit.net runner for VS2012 extension：
在 VS2012 的選單－[Tools] → [Extensions and Updates]，搜尋「xUnit Test Runner」並安裝，然後重啟 VS2012 即可。

o 利用 NuGet 安裝 xUnit.NET：
這裡要注意的是，NuGet 套件管理員所安裝的套件是依附於 Solution/Projects 之內的。所以需要先新增一個 Solution/Project 的測試專案，然後再於該專案內右鍵點選「Manage NuGet Package ...」，搜尋「xUnit.NET」並安裝，隨即會安裝 xUnit test frameowkr 於該 Solution/Project 內並會自動新增其參考 (reference)。

※ 其實那只是下載 xunit.dll 並新增對其的參考。建議是安裝於單一測試專案內，而不是安裝於整個 solution 內。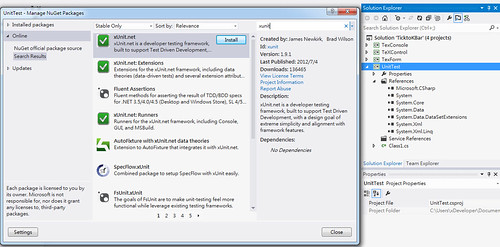

o 撰寫簡單的測試程式，並於 Test Explorer 內執行測試方法並觀察結果。

using Xunit;
public class MyTests
{
    [Fact]
    public void MyTest()
    {
        Assert.Equal(4, 2 + 2);
    }
}

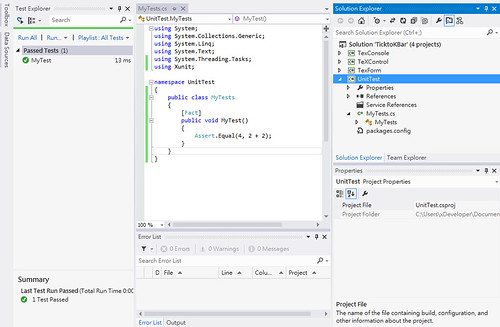
转自：http://www.kenming.idv.tw/install_xunit_test-framework_at_vs2012