POJ 1149 - PIGS - [最大流构图]

Time Limit: 1000MS Memory Limit: 10000K

Description

Mirko works on a pig farm that consists of M locked pig-houses and Mirko can't unlock any pighouse because he doesn't have the keys. Customers come to the farm one after another. Each of them has keys to some pig-houses and wants to buy a certain number of pigs. 
All data concerning customers planning to visit the farm on that particular day are available to Mirko early in the morning so that he can make a sales-plan in order to maximize the number of pigs sold. 
More precisely, the procedure is as following: the customer arrives, opens all pig-houses to which he has the key, Mirko sells a certain number of pigs from all the unlocked pig-houses to him, and, if Mirko wants, he can redistribute the remaining pigs across the unlocked pig-houses. 
An unlimited number of pigs can be placed in every pig-house. 
Write a program that will find the maximum number of pigs that he can sell on that day.

Input

The first line of input contains two integers M and N, 1 <= M <= 1000, 1 <= N <= 100, number of pighouses and number of customers. Pig houses are numbered from 1 to M and customers are numbered from 1 to N. 
The next line contains M integeres, for each pig-house initial number of pigs. The number of pigs in each pig-house is greater or equal to 0 and less or equal to 1000. 
The next N lines contains records about the customers in the following form ( record about the i-th customer is written in the (i+2)-th line): 
A K1 K2 ... KA B It means that this customer has key to the pig-houses marked with the numbers K1, K2, ..., KA (sorted nondecreasingly ) and that he wants to buy B pigs. Numbers A and B can be equal to 0.

Output

The first and only line of the output should contain the number of sold pigs.

Sample Input

3 3
3 1 10
2 1 2 2
2 1 3 3
1 2 6

Sample Output

7

从网上找了本宝典：[网络流建模汇总][Edelweiss].pdf，第一题就是这道题，看了之后那是恍然大悟，有一种醍醐灌顶的感觉，仿佛找寻到了最大流建图的入门诀窍

里面的描述是这样的：

华丽丽的分割线                                                                                                 begin

【题目大意】

有 M 个猪圈，每个猪圈里初始时有若干头猪。一开始所有猪圈都是关闭的。

依次来了 N 个顾客，每个顾客分别会打开指定的几个猪圈，从中买若干头猪。

每个顾客分别都有他能够买的数量的上限。每个顾客走后，他打开的那些猪圈中的猪，都可以被任意地调换到其它开着的猪圈里，然后所有猪圈重新关上。

问总共最多能卖出多少头猪。（1 <= N <= 100, 1 <= M <= 1000）

举个例子来说。有 3 个猪圈，初始时分别有 3、 1 和 10 头猪。

依次来了 3 个顾客，

第一个打开 1 号和 2 号猪圈，最多买 2 头；

第二个打开 1 号和 3 号猪圈，最多买 3 头；

第三个打开 2 号猪圈，最多买 6 头。

那么，最好的可能性之一就是第一个 顾客从 1 号圈买 2 头，然后把 1 号圈剩下的 1 头放到 2 号圈；

第二个顾客从 3 号圈买 3 头；

第三个顾客从 2 号圈买 2 头。

总共卖出 2+3+2=7 头。

【建模方法】 不难想象，这个问题的网络模型可以很直观地构造出来。就拿上面的例子来说， 可以构造出图 1 所示的模型（图中凡是没有标数字的边，容量都是∞）：

• 三个顾客，就有三轮交易，每一轮分别都有 3 个猪圈和 1 个顾客的结点。
• 从源点到第一轮的各个猪圈各有一条边，容量就是各个猪圈里的猪的初始 数量。

• 从各个顾客到汇点各有一条边，容量就是各个顾客能买的数量上限。

• 在某一轮中，从该顾客打开的所有猪圈都有一条边连向该顾客，容量都是 ∞。

• 最后一轮除外，从每一轮的 i 号猪圈都有一条边连向下一轮的 i 号猪圈， 容量都是∞，表示这一轮剩下的猪可以留到下一轮。

• 最后一轮除外，从每一轮被打开的所有猪圈，到下一轮的同样这些猪圈， 两两之间都要连一条边，表示它们之间可以任意流通。

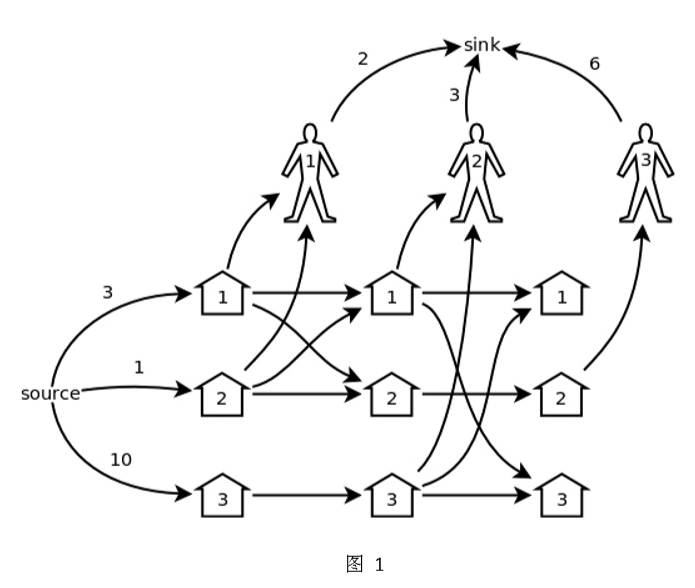
这个网络模型的最大流量就是最多能卖出的数量。图中最多有 2+N+M×N≈100,000 个结点。

这个模型虽然很直观，但是结点数太多了，计算速 度肯定会很慢。

其实不用再想别的算法，就让我们继续上面的例子，用合并的方 法来简化这个网络模型。

首先，最后一轮中没有打开的猪圈就可以从图中删掉了，也就是图 2 中红色 的部分，显然它们对整个网络的流量没有任何影响。

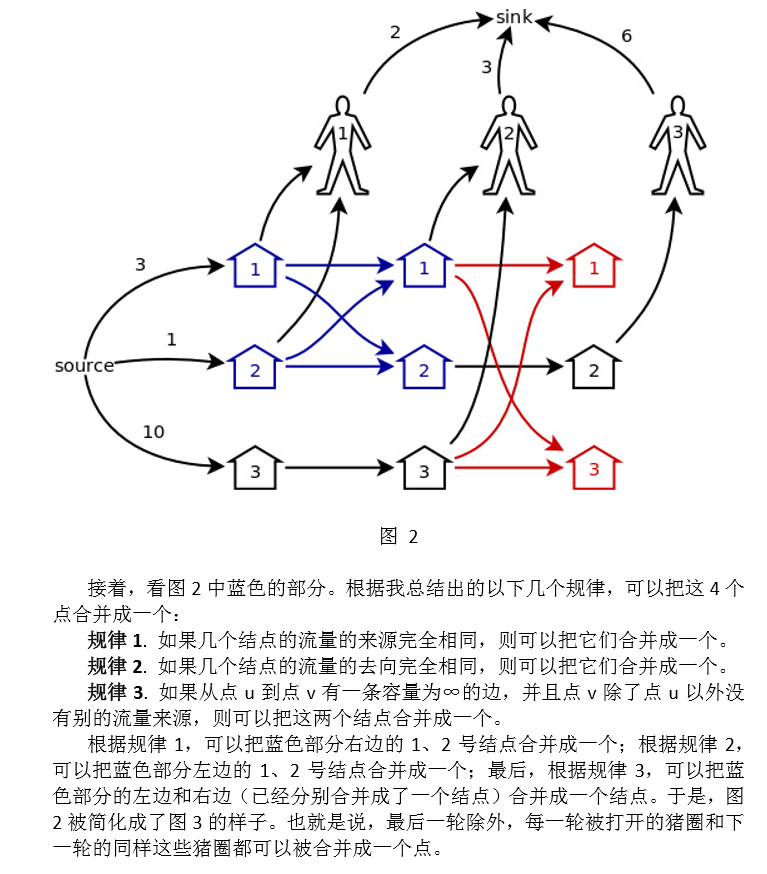
虽然我觉得他的思路非常的exciting，但是这里的三个简化规律我并不完全认同，网上也有一些人认为这三个规律有问题；就当他是对的吧，反正也想不出更好的简化办法……

但是我们先不管继续看下去：

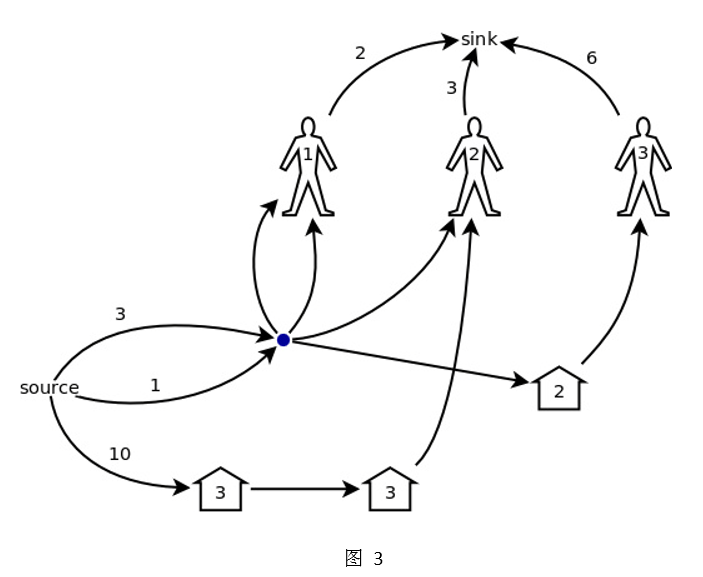
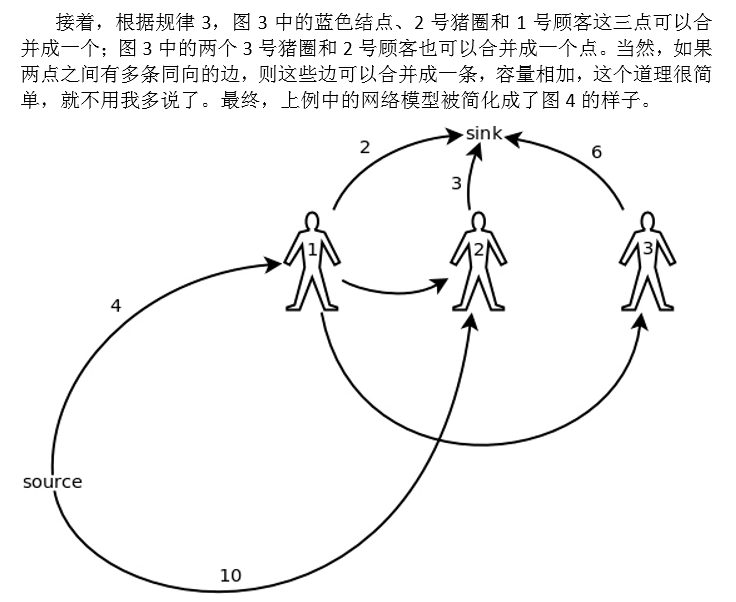
让我们从图 4 中重新总结一下构造这个网络模型的规则：

• 每个顾客分别用一个结点来表示。

• 对于每个猪圈的第一个顾客，从源点向他连一条边，容量就是该猪圈里的猪的初始数量。如果从源点到一名顾客有多条边，则可以把它们合并成一条，容量相加。

• 对于每个猪圈，假设有 n 个顾客打开过它，则对所有整数 i∈[1, n)，从该 猪圈的第 i 个顾客向第 i + 1 个顾客连一条边，容量为∞。

• 从各个顾客到汇点各有一条边，容量是各个顾客能买的数量上限。

•  拿我们前面一直在讲的例子来说：

　　1 号猪圈的第一个顾客是 1 号顾客，所以 从源点到 1 号顾客有一条容量为 3 的边；

　　1 号猪圈的第二个顾客是 2 号顾客，因 此从 1 号顾客到 2 号顾客有一条容量为∞的边；

　　2 号猪圈的第一个顾客也是 1 号 顾客，所以从源点到 1 号顾客有一条容量为 1 的边，和之前已有的一条边合并起 来，容量变成 4；

　　2 号猪圈的第二个顾客是 3 号顾客，因此从 1 号顾客到 3 号顾 客有一条容量为∞的边；

　　3 号猪圈的第一个顾客是 2 号顾客，所以从源点到 2 号 顾客有一条容量为 10 的边。

新的网络模型中最多只有 2 + N = 102 个结点，计算速度就可以相当快了。

可以这样理解这个新的网络模型：

　　对于某一个顾客，如果他打开了猪圈 h，则在他走后，他打开的所有猪圈里剩下的猪都有可能被换到 h 中，因而这些猪都有可能被 h 的下一个顾客买走。

　　所以对于一个顾客打开的所有猪圈，从该顾客到各猪圈的下一个顾客，都要连一条容量为∞的边。

华丽丽的分割线                                                                                                 end

嗯，其实我觉得最后这两句话才是精髓，这是本题一个相当优秀的模型，简练而不失准确；

刚拿到题目可以想象，我们很一下子就想出这样的模型，但是通过对于一个原始而粗糙的模型的简化、归纳，进而寻找规律（尽管这一步中，可能会出现一些问题）；

最后我们得到一个较为简洁明了的模型后，我们可以直接对这个模型进行验证，而不需要花大量时间在验证化简过程上。

在这样的模型指导下，代码就不是很难了……

（PS.由于Dinic算法对于重边的支持，所以我就没有像上面讲的那样，对重边进行合并……反正没几条边……我比较了一下合并和没合并的也没慢多少……）

 #include<cstdio>
 #include<cstdio>
 #include<cstring>
 #include<vector>
 #include<queue>
 #define MAXM 1003
 #define MAXN 103
 #define INF 0x3f3f3f3f
 using namespace std;
 struct Edge{
     int u,v,c,f;
 };
 struct Dinic
 {
     int s,t;
     vector<Edge> E;
     vector<int> G[MAXN];
     bool vis[MAXN]; //BFS使用
     int lev[MAXN];//记录层次
     int cur[MAXN]; //当前弧下标
     void addedge(int from,int to,int cap)
     {
         E.push_back((Edge){from,to,cap,});
         E.push_back((Edge){to,from,,});
         int m=E.size();
         G[from].push_back(m-);
         G[to].push_back(m-);
     }
     bool bfs()
     {
         memset(vis,,sizeof(vis));
         queue<int> q;
         q.push(s);
         lev[s]=;
         vis[s]=;
         while(!q.empty())
         {
             int now=q.front(); q.pop();
             for(int i=;i<G[now].size();i++)
             {
                 Edge edge=E[G[now][i]];
                 int nex=edge.v;
                 if(!vis[nex] && edge.c>edge.f)//属于残存网络的边
                 {
                     lev[nex]=lev[now]+;
                     q.push(nex);
                     vis[nex]=;
                 }
             }
         }
         return vis[t];
     }
     int dfs(int now,int aug)//now表示当前结点，aug表示目前为止的最小残量
     {
         if(now==t || aug==) return aug;//aug等于0时及时退出，此时相当于断路了
         int flow=,f;
         for(int& i=cur[now];i<G[now].size();i++)//从上次考虑的弧开始，注意要使用引用，同时修改cur[now]
         {
             Edge& edge=E[G[now][i]];
             int nex=edge.v;
             if(lev[now]+ == lev[nex] && (f=dfs(nex,min(aug,edge.c-edge.f)))>)
             {
                 edge.f+=f;
                 E[G[now][i]^].f-=f;
                 flow+=f;
                 aug-=f;
                 if(!aug) break;//aug等于0及时退出，当aug!=0,说明当前节点还存在另一个增广路分支
             }
         }
         return flow;
     }
     int maxflow()//主过程
     {
         int flow=;
         while(bfs())//不停地用bfs构造分层网络，然后用dfs沿着阻塞流增广
         {
             memset(cur,,sizeof(cur));
             flow+=dfs(s,INF);
         }
         return flow;
     }
 }dinic;
 int m,n;
 int pighouse[MAXM];//record the initial number of pigs in each pighouse
 int vis[MAXM];//如果这个猪圈已经有了第一个顾客，就标记
 int map[MAXN][MAXN];
 int main()
 {
     memset(vis,,sizeof(vis));
     memset(map,,sizeof(map));
     scanf("%d%d",&m,&n);//m pighouses, n customers
     dinic.s=, dinic.t=n+;
     for(int i=;i<=m;i++) scanf("%d",&pighouse[i]);
     for(int cus_id=;cus_id<=n;cus_id++)
     {
         int A,B,num;
         scanf("%d",&A);
         for(int j=;j<=A;j++)
         {
             scanf("%d",&num);
             if(!vis[num])//cus_id号顾客是num号pighouse的第一个顾客
             {
                 dinic.addedge(dinic.s,cus_id,pighouse[num]);
                 vis[num]=cus_id;//标记为customer的id，方便后面使用
             }
             else
             {
                 dinic.addedge(vis[num],cus_id,INF);
                 vis[num]=cus_id;
             }
         }
         scanf("%d",&B);
         if(B==) continue;
         dinic.addedge(cus_id,dinic.t,B);
     }
     printf("%d\n",dinic.maxflow());
 }

最大流的题，做起来真是让人心情愉悦呢妈个鸡如果不算把vis数组定义成bool类型然后WA5发的话，草草草……