逆向---02.je & jmp & jnz 、OD调试

上一篇：逆向---01.Nop、中文字符串搜索、保存修改后程序

OD调试基础：（01、02篇练手工具：https://pan.baidu.com/s/1kW2qlCz）

nop是删除跳转，你别问我，我看不见也听不见

je是条件跳转，满足条件就跳转，不满足就不跳转

jnz也是条件跳转，不满足条件就跳转

jmp是无条件跳转，管你啥呢，先跳再说

 （姑且可以这么理解）

快捷键：F2下断点、F8单步执行，F9运行，重新载入：点 << 按键 （在工具栏下方的图标栏中）

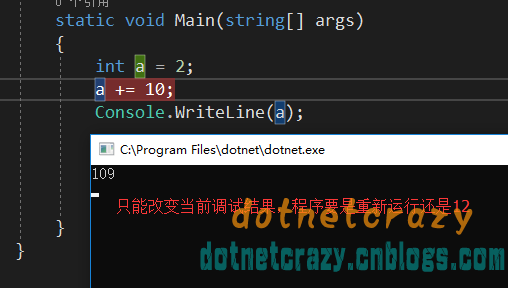
EIP是32位机的指令寄存器，Z标志位1~真，0~假（案例中1代表je跳转实现，0代表je跳转不实现）

OD寄存器修改或者标志位修改是不能保存修改的，一般用于调试（类似于VS调试时自己临时改变量的值，程序重新运行该怎么滴还怎么滴）

举个应用的栗子：

文章中有太基础部分如果看不懂就看上一篇

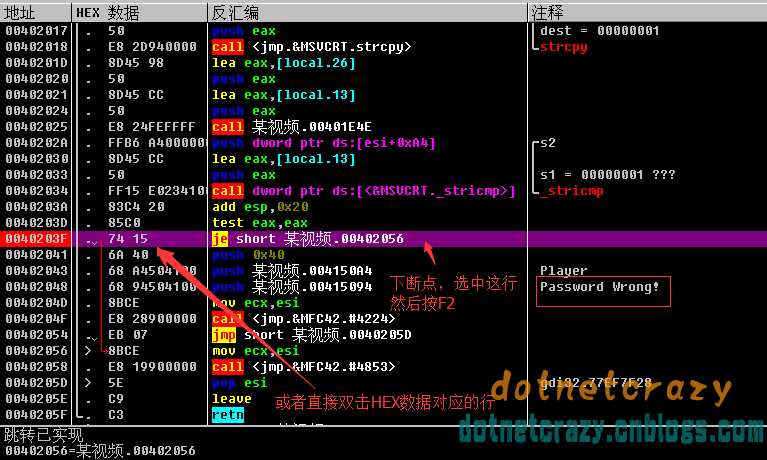
这是一个老版本的视频播放软件（有加密功能），先找关键词，Wrong (最好大小写一样)

字符串搜索后双击打开

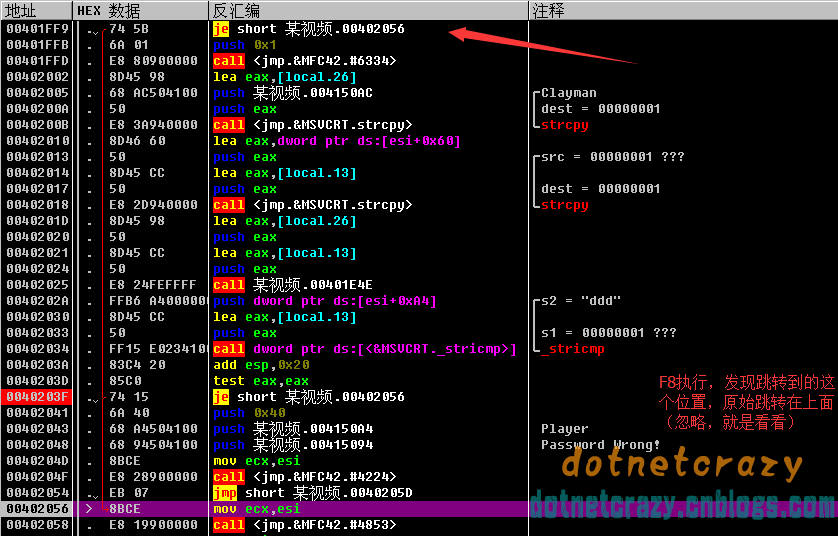
发现上面有一个跳转，下个断点看看F2（HEX数据窗口对应行处双击也可以），然后运行F9

扩充，断点有没有实现不是直接看，得调试的过程中看（红色跳转线代表跳转实现，灰色的代表跳转没实现）

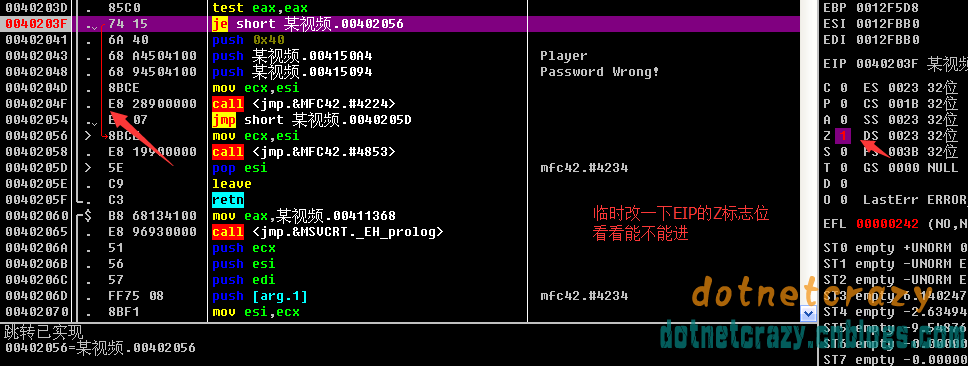
先Z标志位改下看看（双击就会取反0》1）Z标志位1~真，0~假（案例中1代表je跳转实现，0代表je跳转不实现）

F9继续运行，发现可以打开播放了，这时候还是伪破解（OD寄存器修改或者标志位修改是不能保存修改的）

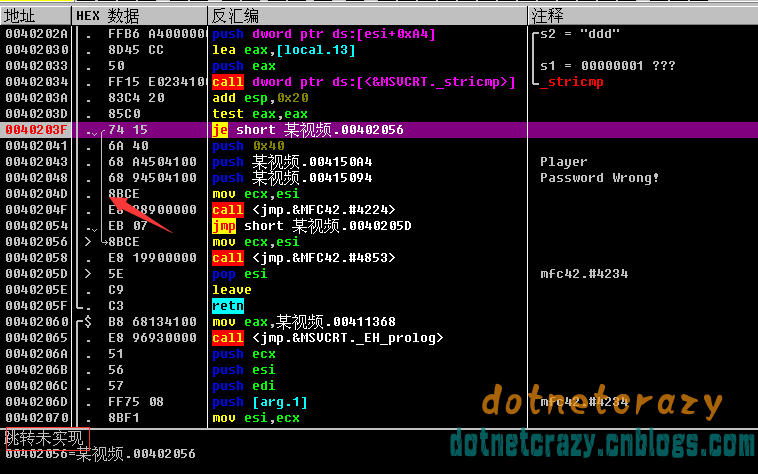
进入正常破解流程，je是条件跳转，想要无条件跳就来个jmp，双击反汇编窗口的这行，把je改成jmp（有些人是 je X0040....，在X前加个0，0x代表十六进制，工具问题可能会把0干掉了）

保存一下，过程从简，不明白的看第一课

KO了

下一篇：逆向---03.mov、test等汇编指令、EAX、关键Call、OD调试技巧