C语言与汇编衔接1

研究实验二

问题研究过程：

发问：C语言中的变量究竟是什么，通过下面的程序进行C语言中的变量的学习

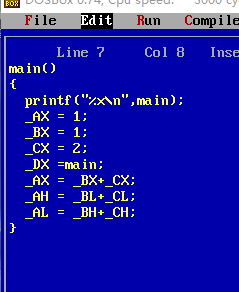
图1  URL.EXE函数

为了研究main函数的首地址，我首先自作聪明的用了一条_DX=main,这样一条语句，希望通过debug中的G命令执行完程序。通过DX的值得到main 的地址。但很不幸的是，最终DX的值为0000，并没有得到相应的程序执行结果。于是发问：

为什么这个程序没有得到执行。那个G命令到底执行了什么？

基于目前对汇编语言的理解，在这里一定要用main这个符号吗，可不可以换成别的符号？来标识所谓的主程序？

于是打算通过单步执行来进一步仔细研究到底发生了什么：

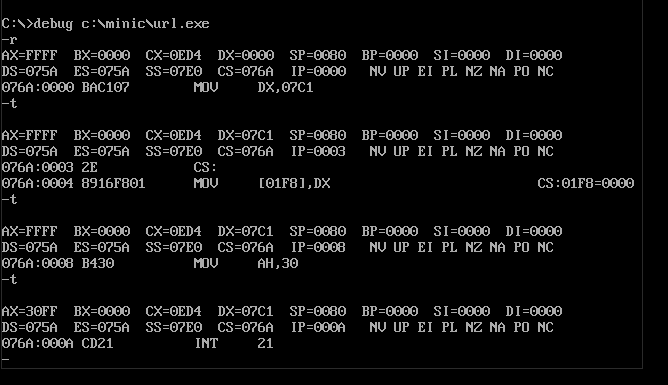
图2  单步执行结果

然而出现了一堆无关的代码，此时并不清楚这些代码是什么，即CS:IP所指的位置并不知道有什么具体用处。研究了很长时间，但是还是没有想到用debug找出URL的main的地址。因此直接进入三

在程序之前补一句代码，如图：

图3  显示main的地址

得到结果：

图4  main 的偏移地址

即得到了main的偏移地址

此处继续发问：

1. 书上所采用的单独写一个函数从原理上讲，并不合理，因为此处的main的地址非彼处的main的地址，没有道理认为两者就是同一个地址

然而事实是：两者的main确实是同一个标志！！！

用u cs:1fa查看，得到：

图5  显示结果

继续研究函数的本质：

图6  子程序调用程序清单

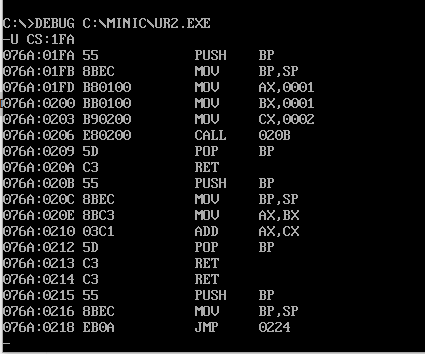
图7  子程序调用过程

可以发现，当执行f();的时候确实是通过call的方式，并且还可以看出，从本质上讲，计算机并不区分什么是主程序，什么是子程序，从汇编代码可以看出，main函数任然是一个被调用的子程序，并没有任何的特殊地位！！

通过研究发现：当把main换成其他标志时，进行编译连接的时候，会报错，于是推测，main是编译环境提供的一个标志，有其对应的固定地址。所以，在此回答上面体术的问题：main都是一样的，其表示的地址是一样的。

总结感悟：

通过实践得出的一个最重要的结论就是，c语言中所谓的函数其实本质就是子程序，即使是所谓的main（）函数，也是如此。而且汇编语言中的寄存器就是C语言中的变量这一概念。不过这些概念在学习汇编和C语言的时候已经形成了，所以对于本次研究，感觉收获并不是很多。