机器学习基石笔记:06 Theory of Generalization








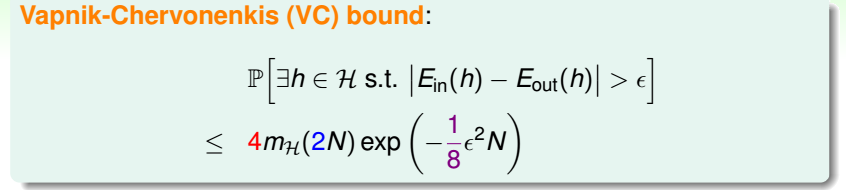
机器学习基石笔记:06 Theory of Generalization的更多相关文章
- 机器学习基石:06 Theory of Generalization
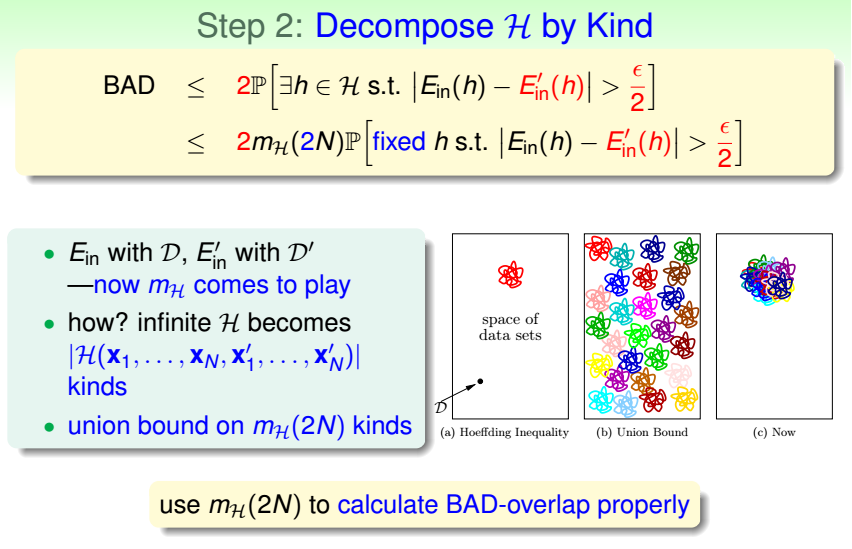
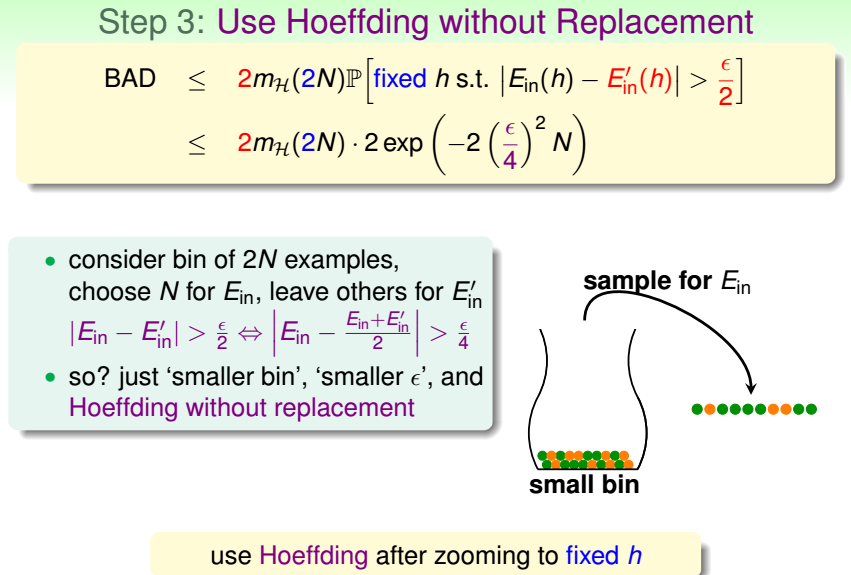
若H的断点为k,即k个数据点不能被H给shatter,那么k+1个数据点也不能被H给shatter,即k+1也是H的断点. 如果给定的样本数N是大于等于k的,易得mH(N)<2N,且随着N的增大 ...
- Coursera台大机器学习课程笔记5 -- Theory of Generalization
本章思路: 根据之前的总结,如果M很大,那么无论假设泛化能力差的概率多小,都无法忽略,所以问题转化为证明M不大,然后上章将其转化为证明成长函数:mh(N)为多项式级别.直接证明似乎很困难,本章继续利用 ...
- 机器学习基石笔记:01 The Learning Problem
原文地址:https://www.jianshu.com/p/bd7cb6c78e5e 什么时候适合用机器学习算法? 存在某种规则/模式,能够使性能提升,比如准确率: 这种规则难以程序化定义,人难以给 ...
- 机器学习基石笔记:04 Feasibility of Learning
原文地址:https://www.jianshu.com/p/f2f4d509060e 机器学习是设计算法\(A\),在假设集合\(H\)里,根据给定数据集\(D\),选出与实际模式\(f\)最为相近 ...
- 林轩田机器学习基石笔记4—Feasibility of Learning
上节课介绍了机器学习可以分为不同的类型.其中,监督式学习中的二元分类和回归分析是最常见的也是最重要的机器学习问题.本节课,我们将介绍机器学习的可行性,讨论问题是否可以使用机器学习来解决. 一.Lear ...
- 林轩田机器学习基石笔记3—Types of Learning
上节课我们主要介绍了解决线性分类问题的一个简单的方法:PLA.PLA能够在平面中选择一条直线将样本数据完全正确分类.而对于线性不可分的情况,可以使用Pocket Algorithm来处理.本节课将主要 ...
- 林轩田机器学习基石笔记2—Learning to Answer Yes/No
机器学习的整个过程:根据模型H,使用演算法A,在训练样本D上进行训练,得到最好的h,其对应的g就是我们最后需要的机器学习的模型函数,一般g接近于目标函数f.本节课将继续深入探讨机器学习问题,介绍感知机 ...
- 林轩田机器学习基石笔记1—The Learning Problem
机器学习分为四步: When Can Machine Learn? Why Can Machine Learn? How Can Machine Learn? How Can Machine Lear ...
- 06 Theory of Generalization
若H的断点为k,即k个数据点不能被H给shatter,那么k+1个数据点也不能被H给shatter,即k+1也是H的断点. 如果给定的样本数N是大于等于k的,易得mH(N)<2N,且随着N的增大 ...
随机推荐
- 记账本,C,Github,entity
package entity; public class Category { private int id; private String name; private int recordNumbe ...
- VS2015秘钥
Visual Studio Professional 2015简体中文版(专业版)KEY:HMGNV-WCYXV-X7G9W-YCX63-B98R2Visual Studio Enterprise 2 ...
- cdn贝四层协议配置端口映射TCP端口转发
端口映射就是将外网主机的IP地址的一个端口映射到内网中一台机器,提供相应的服务.当用户访问该IP的这个端口时,服务器自动将请求映射到对应局域网内部的机器上.端口映射有动态和静态之分 1.安装好节点后初 ...
- 515. Find Largest Value in Each Tree Row查找一行中的最大值
[抄题]: You need to find the largest value in each row of a binary tree. Example: Input: 1 / \ 3 2 / \ ...
- Head First Servlets & JSP 学习笔记 第十三章 —— 过滤器的威力
过滤器可能是最强大的Web应用开发工具了! 与Servlet非常类似,过滤器就是Java组件,请求发送到Servlet之前,可以用过滤器截获和处理请求:另外Servlet结束工作之后,但在响应发回给客 ...
- Socket 多线程编程
前面一片学习了TCP/IP的基础网络编程,并给出了简单的服务端与客户端通信交互的例子.还介绍了UPC的通信例子. 这次学习TCP/IP的多线程编程.因为涉及到TCP/IP一般都是多线程,服务端会一直监 ...
- git创建新的分支
1.本地创建一个新的分支 git branch develop 2.切换到新创建的分支 git checkout develop 3.将新的分支发布到gitlab上 git push origin d ...
- Spring Boot 整合mybatis 使用多数据源
本人想要实现一个项目里面多个数据库源连接,所以就尝试写一个demo,不多说,先贴结构,再贴代码,可以根据以下的顺序,直接copy解决问题. 首先,dao和resource下的mappers可以用myb ...
- 搭建RESTful API来使用Fabric Node SDK 开篇
在Balance-Transfer中,有关于Node SDK比较完备的例子. SDK的官方文档在这里:https://fabric-sdk-node.github.io/ Balance-Transf ...
- Linux 6上使用UDEV绑定共享存储
1.硬盘的查看方式 [root@cl6-11gr2-rac1 ~]# ls -ltr /dev/sd* brw-rw----. 1 root disk 8, 48 8月 16 13:34 /dev/s ...
