图之强连通、强连通图、强连通分量 Tarjan算法

原文地址：https://blog.csdn.net/qq_16234613/article/details/77431043

一、解释

在有向图G中，如果两个顶点间至少存在一条互相可达路径，称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。 
求解有向图的强连通分量算法有很多，例如Kosaraju，Gabow和Tarjan算法，其中Gabow和Tarjan算法时间复杂度要优于Kosaraju。 
理解： 
如果单纯将其看出图的话有点难以理解，但是当我们将其看成树，就很容易了。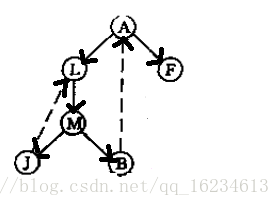 
 
如上图，如果两个点成强联通，那么显然在树中就会存在一个环，图中L-M-J-L和A-L-M-B-A成环所以组成的强联通分量。

二、Tarjan算法

Tarjan算法基于深度优先搜索树，其有两个重要变量DFN[u]：表示在深度搜索中遍历到该节点的次序。LOW(u)表示以u节点为树根，u及u以下树节点所能找到的最小次序号。注意Tarjan认为单个节点自身就是一个强联通分量，在处理数据时注意屏蔽。以上图为例，我们从A开始， 
A：DFN[1] = 1； LOW(1)=1 
L：DFN[2] = 2； LOW(2)=2 
M：DFN[3] = 3； LOW(3)=3 
J：DFN[4] = 4； LOW(4)=4 
这时我们在J节点继续往下搜索时，发现L节点我们已经搜索过了，且L：LOW(2)=2，我们发现J：LOW(4)=4>L：LOW(2)=2,因此我们将其赋值LOW(4)=2，这说明此时我们发现了一个环，代表一个强联通分量。 
下面继续： 
J：DFN[4] = 4； LOW(4)=2 
M：DFN[3] = 3； LOW(3)=2 
B：DFN[5] = 4； LOW(5)=5 
发现B到A： 
B：DFN[5] = 4； LOW(5)=1 
开始返回更新： 
M：DFN[3] = 3； LOW(3)=1 
L：DFN[2] = 2； LOW(2)=1 
A：DFN[1] = 1； LOW(1)=1 
发现DFN=LOW(1)，弹出栈。

void tarjan(int u){

    DFN[u]=LOW[u]=++time; //次序从1开始，初始时由于默认将DFN[u]=LOW[u]都置为次序号
    // 将当前节点压栈，置位在栈中，已访问。
    visit[u]=;
    s.push(u);
    instack[u]=;

    //取u节点的下一路径节点v,当没有v可取时也说明深度搜索已经到达当前最底部，这是我们函数返回寻找另一条路径。
    for(int j=;j<G[u].size();j++){
        int v=G[u][j];
        if(visit[v]==){
            tarjan(v);
            // 在深度搜索返回时，如果v节点下存在子树，要将u节点的LOW[u]更新。
            LOW[u]=min(LOW[u],LOW[v]);
        }
        else if(instack[v]){
            // v节点已经被访问，并且在栈中，说明在当前路径上存在环，此处只是赋值，但并不代表在u子树的底下的多个节点没有比当前环更大的环。无法作为深度终止条件。
            LOW[u]=min(LOW[u],DFN[v]);
        }
    }

    int m;
    int num=; //对一个环计数计数
    // 在深度搜索完结后返回时，判断DFN[u]==LOW[u]，相等说明找到了一个环，将栈中节点弹出。注意tarjan算法认为单个节点也为环。
    if(DFN[u]==LOW[u]){
        // 将栈中节点弹出，并计数
        do{
            m=s.top();
            s.pop();
            instack[m]=;
            num++;
        }while(m!=u);

        // 只有环内节点数大于两个才是真正环。
        if(num>){
            // n个点两两相交（互相到达），则有n*(n-1)/2条连接线
            total+=num*(num-)/;
        }
    }

}

关于为啥只用访问一次： 
开始疑惑，肯定会多条路径通过某一点，如果用visit记录访问记录的话，下一条路径不就会不能访问该点了吗？遂绘制丑图：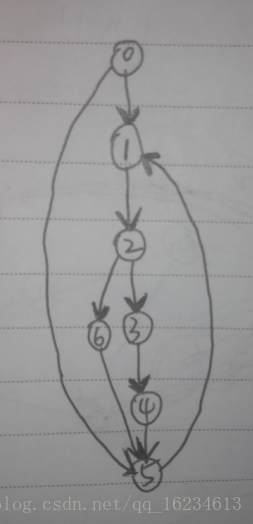 
 
如图当我们访问到6节点时发现有环，且到达底点，这时根据算法开始返回，同时将2-6-5这条环也遍历掉（此时5号已访问压栈且有LOW=1）。也就是说在返回到1号节点开始出栈时，我们已经把1号节点的子树全部访问了一遍，该成环的也做了标记。在1号节点下的子节点不会通向1号节点以上的节点，比如0号节点，不然1号只能算一个类似于2-6-5这条环。至于从0号到5号就不用再判断了。所以遍历一遍就行。我觉得巧妙之处在于在深度向前搜索过程并没有处理数据，而在深度返回过程中开始更新数据，记录找到的回路，并且到达子树根节点DFN[u]==LOW[u]才开始出栈。