Ouroboros Snake POJ - 1392（数位哈密顿回路）

看hdu 2894的题意  两个题一样

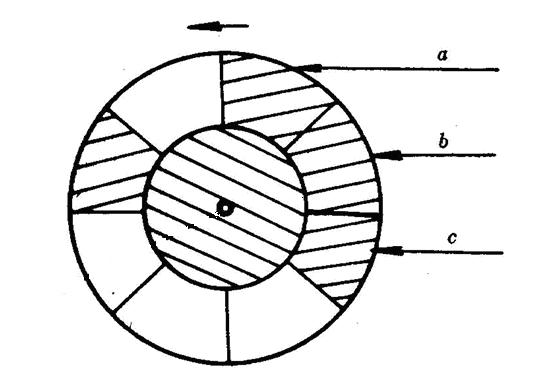
旋转鼓的表面分成m块扇形,如图所示(m=8)。图中阴影区表示用导电材料制成,空白区用绝缘材料制成,终端a、b和c是3（k=3）处接地或不是接地分别用二进制信号0或1表示。因此,鼓的位置可用二进制信号表示。试问应如何选取这8个扇形的材料使每转过一个扇形都得到一个不同的二进制信号,即每转一周,能得到000到111的8个数。

那我们现在把旋转鼓的表面分成m块扇形，每一份记为0或1，使得任何相继的k个数的有序组（按同一方向）都不同（就是这个2^m位的有序组  从每个位向后取k位 所组成的数的集合 即为0 ~ 2^(m - 1)），对固定的k，m最大可达到多少，并任意输出符合条件的一个这样的有序组。

这个题是先找出有序组 然后求第k个下标开始的n位数是多少

这个题和上题字母不同 这里n代表上题的k  k为第k位

解析：

　　想一下，n位二进制数是不是有2ⁿ种情况，那么对于那个2ⁿ位的数，我们起点从下标0开始取n位，然后起点每次都向后移一位，终点也后移一位，就这样对应了0~2^n-1 这些数

我们把每个长度位n的子串看做一个点，把 0 和 1 看成边，那么两个点  例如 0 ~（n-1）  和  1 ~ n  这两个点 如何联通的呢

当然是 0 ~ （n-1）位左移一位 再 + 1 或 0  得出1 ~ n 的

（u 到 v 时 起点后移一位 终点后移一位 ）

然后fleury就能求出字典序最小的路径

然后。。。别忘了它是一个循环吖，那么再在这个求出来的路径后边加上前 n-1 位使之构成循环  求第k个就好了

就是可以理解为：

前n个数为一个点u   后n个数为一个点v

u通过边1或0通往v和v’

求边所组成路径的最小序列

#include <iostream>
#include <cstdio>
#include <sstream>
#include <cstring>
#include <map>
#include <cctype>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
#include <cmath>
#include <bitset>
#define rap(i, a, n) for(int i=a; i<=n; i++)
#define rep(i, a, n) for(int i=a; i<n; i++)
#define lap(i, a, n) for(int i=n; i>=a; i--)
#define lep(i, a, n) for(int i=n; i>a; i--)
#define rd(a) scanf("%d", &a)
#define rlld(a) scanf("%lld", &a)
#define rc(a) scanf("%c", &a)
#define rs(a) scanf("%s", a)
#define pd(a) printf("%d\n", a);
#define plld(a) printf("%lld\n", a);
#define pc(a) printf("%c\n", a);
#define ps(a) printf("%s\n", a);
#define MOD 2018
#define LL long long
#define ULL unsigned long long
#define Pair pair<int, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define _  ios_base::sync_with_stdio(0),cin.tie(0)
//freopen("1.txt", "r", stdin);
using namespace std;
const int maxn = , INF = 0x7fffffff, LL_INF = 0x7fffffffffffffff;
int f[ << maxn], vis[ << maxn][], stk[ << maxn];
int n, k, tot;

void fleury(int u)
{
    for(int i = ; i <= ; i++)
    {
        if(!vis[u][i])
        {
            vis[u][i] = ;
            fleury(((u << ) + i) % f[n - ]);
            stk[tot++] = i;
        }
    }
}

int main()
{
    f[] = ;
    for(int i = ; i < ; i++)
        f[i] = f[i-] * ;
    while(cin >> n >> k && n + k)
    {
        mem(vis, );
        mem(stk, );
        tot = ;
        fleury();
        tot += n - ;
        tot -= k;
        int res = ;
        for(int i = ; i < n; i++)
            res = (res << ) + stk[tot - i];      // 别忘了这是一个栈 从后向前哩
        cout << res << endl;

    }

    return ;
}