样本失衡会对SVM的影响

假设正类样本远多于负类

1、线性可分的情况

假设真实数据集如下：

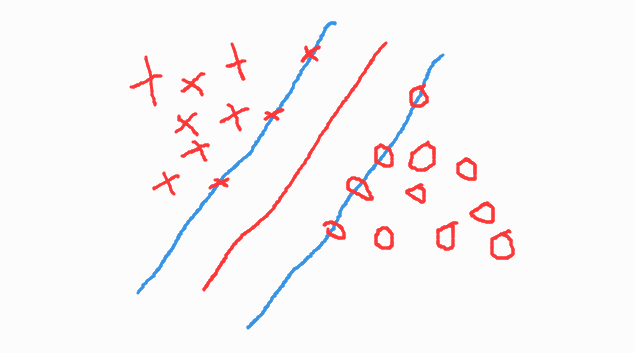
由于负类样本量太少，可能会出现下面这种情况

使得分隔超平面偏向负类。严格意义上，这种样本不平衡不是因为样本数量的问题，而是因为边界点发生了变化

2、线性不可分的情况

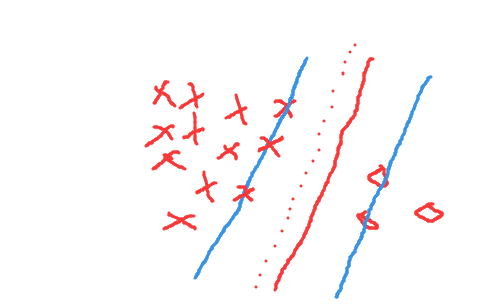
源数据以及理想的超平面情况如下：

很可能由于负类样本太少出现以下这种情况，超平面偏向负类

---

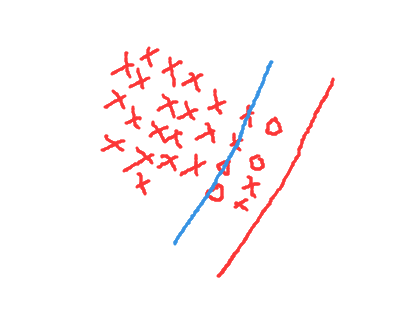
解决不平衡的方案：

【SVM对不平衡本身并不十分敏感】

【SVM的超平面只与支持向量有关，因此原离决策超平面的数据的多少并不重要】

1、过抽样（随机过抽样）

2、欠抽样（对多数类边界样本进行采样）（既能代表多数类样本分布特征, 又能对分类界面有一定影响的样本特性欠取样方法）

3、改进算法本身（代价敏感）

---

参考博客

　　   1)、对正例和负例赋予不同的C值，例如正例远少于负例，则正例的C值取得较大，这种方法的缺点是可能会偏离原始数据的概率分布；

2)、对训练集的数据进行预处理即对数量少的样本以某种策略进行采样，增加其数量或者减少数量多的样本，典型的方法如：随机插入法，缺点是可能出现

overfitting，较好的是：Synthetic Minority Over-sampling TEchnique(SMOTE)，其缺点是只能应用在具体的特征空间中，不适合处理那些无法用

特征向量表示的问题，当然增加样本也意味着训练时间可能增加；

3)、基于核函数的不平衡数据处理。