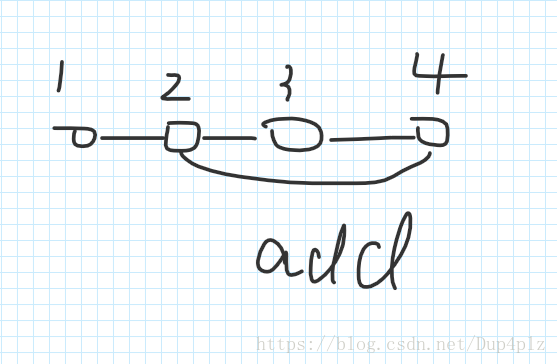HDU - 4081 Qin Shi Huang's National Road System 【次小生成树】

题目链接

http://acm.hdu.edu.cn/showproblem.php?pid=4081

题意

给出n个城市的坐标 以及 每个城市里面有多少人

秦始皇想造路 让每个城市都连通 （直接或者间接都可以）

然后 有一个特别厉害的大臣 可以造一条魔法路 不用耗费资金 但是要求 这条路链接的两座城市的人要尽量多

定义了一个 value = A/B

A = 魔法路链接的两座城市的总人数

B = 除了魔法路，其他路的总权值

求出最大的value

思路

首先我会想到最小生成树

然后我想让value 最大 我就想 能不能 去枚举每一条边 当做 魔法路

因为 求最小生成树 要保证 value 尽量小

然后枚举每一条边的时候

如果这条边已经在最小生成树里面了 那么此时的ans = (A[i] + A[j] / ans - G[i][j])

B = 答案 - 这条边

这个应该比较好理解

如果没有在最小生成树里面 ，那么此时的B = ans - Max[i][j]

为什么是这样呢。。

Max[i][j] 表示 从i - j 的最大边

因为 我们枚举的这条边 没有在 这条边 所以加入这条边之后 i - j 之间 就会形成一个环路

比如说 是这样的

自然就可以发现 我们在 2 - 4 之间已经在最小生成树里面的边 可以拆掉一条

那么拆哪一条呢，， 为了对答案有更大贡献，自然是边权最大的那条

AC代码

#include <cstdio>
#include <cstring>
#include <ctype.h>
#include <cstdlib>
#include <cmath>
#include <climits>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <map>
#include <stack>
#include <set>
#include <list>
#include <numeric>
#include <sstream>
#include <iomanip>
#include <limits>

#define CLR(a, b) memset(a, (b), sizeof(a))
#define pb push_back
#define bug puts("***bug***");
#define fi first
#define se second
#define stack_expand #pragma comment(linker, "/STACK:102400000,102400000")
#define syn_close   ios::sync_with_stdio(false);cin.tie(0);
//#define bug
//#define gets gets_s

using namespace std;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair <int, int> pii;
typedef pair <ll, ll> pll;
typedef pair <string, int> psi;
typedef pair <string, string> pss;
typedef pair <double, int> pdi;

const double PI = acos(-1.0);
const double E = exp(1.0);
const double eps = 1e-8;

const int INF = 0x3f3f3f3f;
const int maxn = 1e3 + 10;
const int MOD = 142857;

int n;
double G[maxn][maxn];

struct node
{
    int x, y, p;
    node() {}
    node(int x, int y, int p) : x(x), y(y), p(p) {}
    void read()
    {
        scanf("%d%d%d", &x, &y, &p);
    }
}point[maxn];

double dis(int a, int b)
{
    double d1 = (point[a].x - point[b].x) * (point[a].x - point[b].x) * 1.0;
    double d2 = (point[a].y - point[b].y) * (point[a].y - point[b].y) * 1.0;
    return sqrt(d1 + d2);
}

int used[maxn][maxn];
double Max[maxn][maxn];
double lowcost[maxn];
int pre[maxn];
int visit[maxn];

double ans;

int findMin()
{
    double Maxc = INF * 1.0;
    int flag = 0;
    for (int i = 1; i <= n; i++)
    {
        if (visit[i] == 0 && lowcost[i] < Maxc)
        {
            Maxc = lowcost[i];
            flag = i;
        }
    }
    return flag;
}

void prime()
{
    for (int i = 1; i <= n; i++)
    {
        visit[i] = 0;
        lowcost[i] = INF * 1.0;
        used[i][i] = 0;
        Max[i][i] = -INF * 1.0;
        for (int j = i + 1; j <= n; j++)
        {
            Max[i][j] = Max[j][i] = -INF * 1.0;
            used[i][j] = used[j][i] = 0;
        }
    }
    for (int i = 1; i <= n; i++)
    {
        lowcost[i] = Max[1][i] = G[1][i];
        pre[i] = 1;
    }
    pre[1] = -1;
    visit[1] = 1;
    ans = 0.0;
    for (int i = 2; i <= n; i++)
    {
        int k = findMin();
        visit[k] = 1;
        ans += lowcost[k];
        used[pre[k]][k] = used[k][pre[k]] = 1;
        for (int j = 1; j <= n; j++)
        {
            if (visit[j] == 1 && j != k)
                Max[j][k] = Max[k][j] = max(Max[j][pre[k]], lowcost[k]);
            if (visit[j] == 0 && lowcost[j] > G[k][j])
            {
                lowcost[j] = G[k][j];
                pre[j] = k;
            }
        }
    }
}

double smst()
{
    double Maxc = 0.0;
    for (int i = 1; i <= n; i++)
        for (int j = i + 1; j <= n; j++)
            if (used[i][j] == 0)
                Maxc = max(Maxc, (point[i].p + point[j].p) * 1.0 / (ans - Max[i][j]));
            else
                Maxc = max(Maxc, (point[i].p + point[j].p) * 1.0 / (ans - G[i][j]));
    return Maxc;
}

void clear()
{
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            G[i][j] = 0.0;
}

int main()
{
    int t;
    cin >> t;
    while (t--)
    {
        scanf("%d", &n);
        clear();
        for (int i = 1; i <= n; i++)
            point[i].read();
        for (int i = 1; i <= n; i++)
            for (int j = i + 1; j <= n; j++)
                G[i][j] = G[j][i] = dis(i, j);
        prime();
        printf("%.2lf\n", smst());
    }
}

/*
    先跑最小生成树
    然后去枚举每一条边 当做 magic road
    如果该边本来就在最小生成树当中 那么我就删去这条边 维护答案
    如果该边本来没有在最小生成树当中，那么我就删去i - j 中的最大边 维护答案
*/