Luogu 3625 [APIO2009]采油区域

想了很久的dp，看了一眼题解之后感觉自己被安排了。

发现从一个矩形中选择三个不相交的正方形一共只有六种取法。

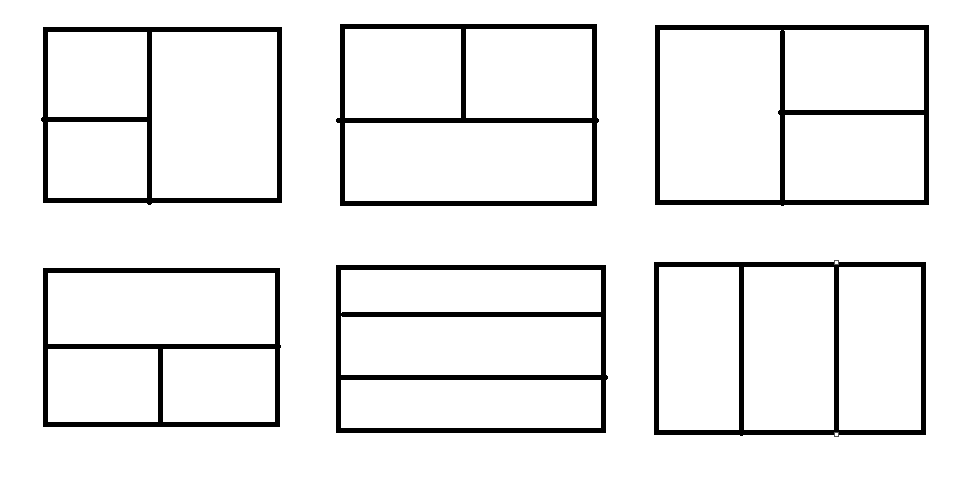
那么我们可以处理出四个值：

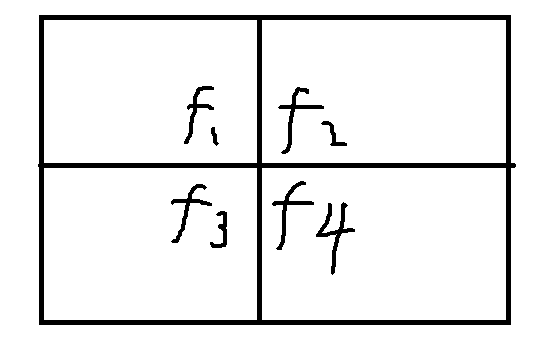
$f_{i, j}$分别表示以$(i, j)$为右下角，左下角，右上角，左上角的矩阵中选一个$k*k$正方形的最大值。

这样就可以算出前四种情况，后两种情况只要乱搞就可以了。

时间复杂度$O(nm)$。

Code：

#include <cstdio>
#include <cstring>
using namespace std;

const int N = ;

int n, m, k, ans, a[N][N], sum[N][N], s[N][N];
int f1[N][N], f2[N][N], f3[N][N], f4[N][N], r[N], c[N];

template <typename T>
inline void read(T &X) {
    X = ; char ch = ; T op = ;
    for(; ch > ''|| ch < ''; ch = getchar())
        if(ch == '-') op = -;
    for(; ch >= '' && ch <= ''; ch = getchar())
        X = (X << ) + (X << ) + ch - ;
    X *= op;
}

inline void chkMax(int &x, int y) {
    if(y > x) x = y;
}

inline int max(int x, int y) {
    return x > y ? x : y;
}

inline int max(int x, int y, int z) {
    return max(max(x, y), z);
}

int main() {
    read(n), read(m), read(k);
    for(int i = ; i <= n; i++)
        for(int j = ; j <= m; j++) {
            read(a[i][j]);
            sum[i][j] = sum[i][j - ] + a[i][j];
        }
    for(int i = ; i <= n; i++)
        for(int j = ; j <= m; j++)
            sum[i][j] += sum[i - ][j];
    for(int i = k; i <= n; i++)
        for(int j = k; j <= m; j++)
            s[i][j] = sum[i][j] + sum[i - k][j - k] - sum[i][j - k] - sum[i - k][j];

/*    for(int i = 1; i <= n; i++, printf("\n"))
        for(int j = 1; j <= m; j++)
            printf("%d ", s[i][j]);      */

    for(int i = ; i <= n; i++)
        for(int j = ; j <= m; j++)
            chkMax(f1[i][j], max(s[i][j], f1[i - ][j], f1[i][j - ]));
    for(int i = ; i <= n; i++)
        for(int j = m; j >= ; j--)
            chkMax(f2[i][j], max(s[i][j + k - ], f2[i - ][j], f2[i][j + ]));
    for(int i = n; i >= ; i--)
        for(int j = m; j >= ; j--)
            chkMax(f3[i][j], max(s[i + k - ][j + k - ], f3[i + ][j], f3[i][j + ]));
    for(int i = n; i >= ; i--)
        for(int j = ; j <= m; j++)
            chkMax(f4[i][j], max(s[i + k - ][j], f4[i + ][j], f4[i][j - ])); 

    ans = ;
    for(int i = k; i <= n - k; i++)
        for(int j = k; j <= m - k; j++) {
            chkMax(ans, f1[i][j] + f2[i][j + ] + f3[i + ][]);
            chkMax(ans, f1[i][j] + f2[n][j + ] + f4[i + ][j]);
            chkMax(ans, f1[n][j] + f2[i][j + ] + f3[i + ][j + ]);
            chkMax(ans, f1[i][m] + f4[i + ][j] + f3[i + ][j + ]);
        }

    for(int i = ; i <= n; i++)
        for(int j = ; j <= m; j++) {
            chkMax(r[i], s[i][j]);
            chkMax(c[j], s[i][j]);
        }

    for(int i = k; i <= n -  * k; i++)
        for(int j = i + k, mid = r[j]; j <= n - k; j++, chkMax(mid, r[j]))
            chkMax(ans, f1[i][m] + mid + f3[j + ][]);
    for(int i = k; i <= m -  * k; i++)
        for(int j = i + k, mid = c[j]; j <= m - k; j++, chkMax(mid, c[j]))
            chkMax(ans, f1[n][i] + mid + f2[n][j + ]);

    printf("%d\n", ans);
    return ;
}