[hdu1402]A * B Problem Plus(NTT)

解题关键：快速数论变换NTT模板。

注意$ans$数组的$ans[n]$一定要注意置$0$，或者结果从$n-1$开始遍历，这里很容易出错。

代码1：ACdreamer 的板子。

为什么要reverse序列至今没证明出来。=，=有懂的聚聚可以告诉本渣一下，万分感谢！！~~

经过聚聚们的指导，还是不太懂，最终从wiki上找到了比较易懂的证明~

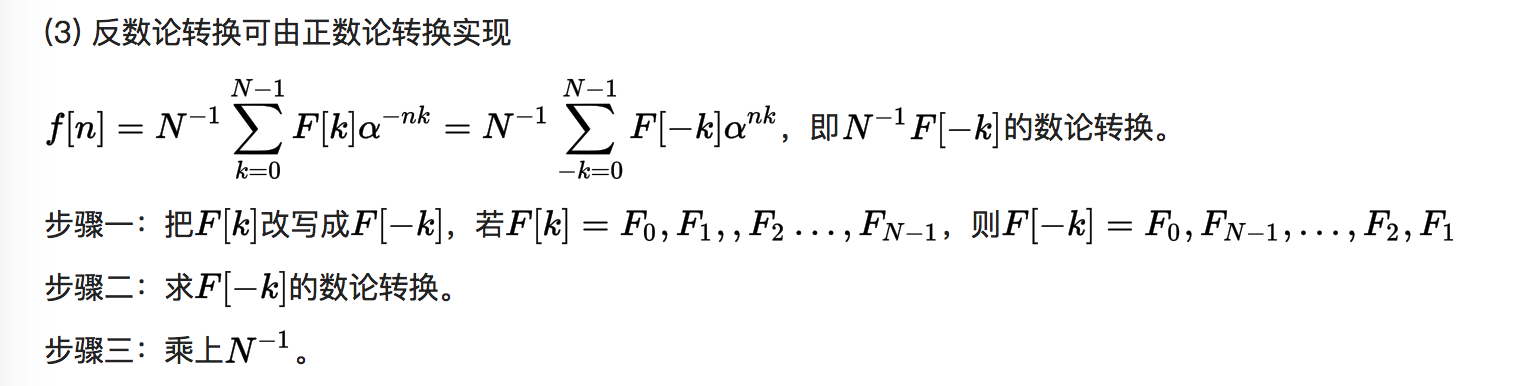
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll;
const int N=;
ll G=,P=,a[*N],b[*N],wn[];//P是费马素数
char s[N],t[N];
ll mod_pow(ll x,ll n,ll p) {
    ll res=;x%=p;
    while(n){
        if(n&) res=res*x%p;
        x=x*x%p;
        n>>=;
    }
    return res;
}
void getwn(){ for(int i=;i<;i++) wn[i]=mod_pow(G,(P-)/(<<i),P);}//预处理w
void NTT(ll x[],int n,int rev){
    ll w,u,v;
    for(int i=,j=;i!=n;i++){//构造逆序表
        if(i>j) swap(x[i],x[j]);
        for(int l=n>>;(j^=l)<l;l>>=);
    }
    for(int i=,ds=;i<n;i<<=,ds++)
        for(int j=;j<n;j+=i){
            w=;
            for(int k=j;k<j+i/;k++,w=w*wn[ds]%P){//蝴蝶操作
                u=x[k]%P;v=w*x[k+i/]%P;
                x[k]=(u+v)%P;
                x[k+i/]=(u-v+P)%P;
            }
        }
    if(rev==-){
        for(int i=;i<n/;i++) swap(x[i],x[n-i]);//把开始的wn求逆元合并到这里来了，通过什么性质至今没搞懂。
        w=mod_pow(n,P-,P);//乘n的逆元
        for(int i=;i<n;i++) x[i]=x[i]*w%P;
    }
}
void solve(){
    int i,n=,les=(int)strlen(s),let=(int)strlen(t);
    while(n<les+let) n<<=;
    for(i=;i<les;i++) a[i]=s[les-i-]-'';
    for(i=les;i<=n;i++) a[i]=;
    for(i=;i<let;i++) b[i]=t[let-i-]-'';
    for(i=let;i<=n;i++) b[i]=;
    NTT(a,n,);NTT(b,n,);
    for (i=;i<n;i++) a[i]=a[i]*b[i]%P;
    NTT(a,n,-);
    for(i=;i<n;i++)
        if(a[i]>=){//if可以不带
            a[i+]+=a[i]/;
            a[i]%=;
        }
    while(n>&&!a[n]) n--;
    for(;n>=;n--) printf("%lld",a[n]);
    printf("\n");
}
int main(){
    getwn();
    while(scanf("%s%s",s,t)!=EOF) solve();
    return ;
}

代码2：

完全按照fft转化而来

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll;
const int N=;
ll G=,P=,a[*N],b[*N],wn[],iwn[];//P是费马素数
char s[N],t[N];
ll mod_pow(ll x,ll n,ll p) {
    ll res=;x%=p;
    while(n){
        if(n&) res=res*x%p;
        x=x*x%p;
        n>>=;
    }
    return res;
}
void getwn(){
    for(int i=;i<;i++) wn[i]=mod_pow(G,(P-)/(<<i),P);
    for(int i=;i<;i++) iwn[i]=mod_pow(wn[i],P-,P);
}//预处理w
void NTT(ll x[],int n,int rev){
    ll w,u,v,wm;
    for(int i=,j=;i!=n;i++){//构造逆序表
        if(i>j) swap(x[i],x[j]);
        for(int l=n>>;(j^=l)<l;l>>=);
    }
    for(int i=,ds=;i<n;i<<=,ds++)
        for(int j=;j<n;j+=i){
            w=;
            if(rev==-) wm=iwn[ds];
            else wm=wn[ds];
            for(int k=j;k<j+i/;k++,w=w*wm%P){//蝴蝶操作
                u=x[k]%P;v=w*x[k+i/]%P;
                x[k]=(u+v)%P;
                x[k+i/]=(u-v+P)%P;
            }
        }
    if(rev==-){
        w=mod_pow(n,P-,P);//乘n的逆元
        for(int i=;i<n;i++) x[i]=x[i]*w%P;
    }
}
void solve(){
    int i,n=,les=(int)strlen(s),let=(int)strlen(t);
    while(n<les+let) n<<=;
    for(i=;i<les;i++) a[i]=s[les-i-]-'';
    for(i=les;i<=n;i++) a[i]=;
    for(i=;i<let;i++) b[i]=t[let-i-]-'';
    for(i=let;i<=n;i++) b[i]=;
    NTT(a,n,);NTT(b,n,);
    for (i=;i<n;i++) a[i]=a[i]*b[i]%P;
    NTT(a,n,-);
    for(i=;i<n;i++)
        if(a[i]>=){//if可以不带
            a[i+]+=a[i]/;
            a[i]%=;
        }
    while(n>&&!a[n]) n--;
    for(;n>=;n--) printf("%lld",a[n]);
    printf("\n");
}
int main(){
    getwn();
    while(scanf("%s%s",s,t)!=EOF) solve();
    return ;
}

FFT常用素数P=r*2^k+1,g为P的原根
P r k g
3 1 1 2
5 1 2 2
17 1 4 3
97 3 5 5
193 3 6 5
257 1 8 3
7681 15 9 17
12289 3 12 11
40961 5 13 3
65537 1 16 3
786433 3 18 10
5767169 11 19 3
7340033 7 20 3
23068673 11 21 3
104857601 25 22 3
167772161 5 25 3
469762049 7 26 3
1004535809 479 21 3
2013265921 15 27 31
2281701377 17 27 3
3221225473 3 30 5
75161927681 35 31 3
77309411329 9 33 7