零难度指南：手把手教你如何通过在线Excel实现资产负债表

前言

作为财务分析中的三大报表之一，资产负债表的作用是展示一个企业在特定时间点上的财务状况。今天小编就为大家介绍一下如何使用葡萄城公司的纯前端在线表格控件SpreadJS实现一个资产负债表。

环境准备

SpreadJS在线Excel体验地址：https://demo.grapecity.com.cn/SpreadJS/WebDesigner/index.html

操作步骤

1）填报

1. 先将本地excel模板导入至SpreadJS中。
   
   

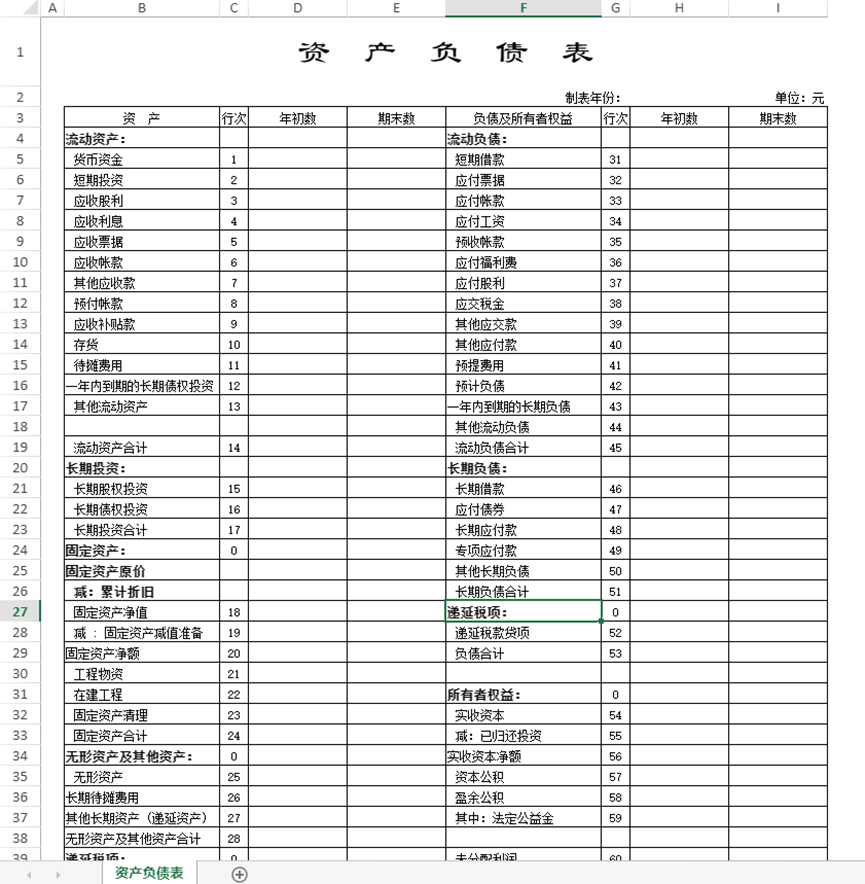
2. 对于合计类单元格，进行简单公式计算的，并且这里的公式是固定的，并设计好背景颜色。
   
   

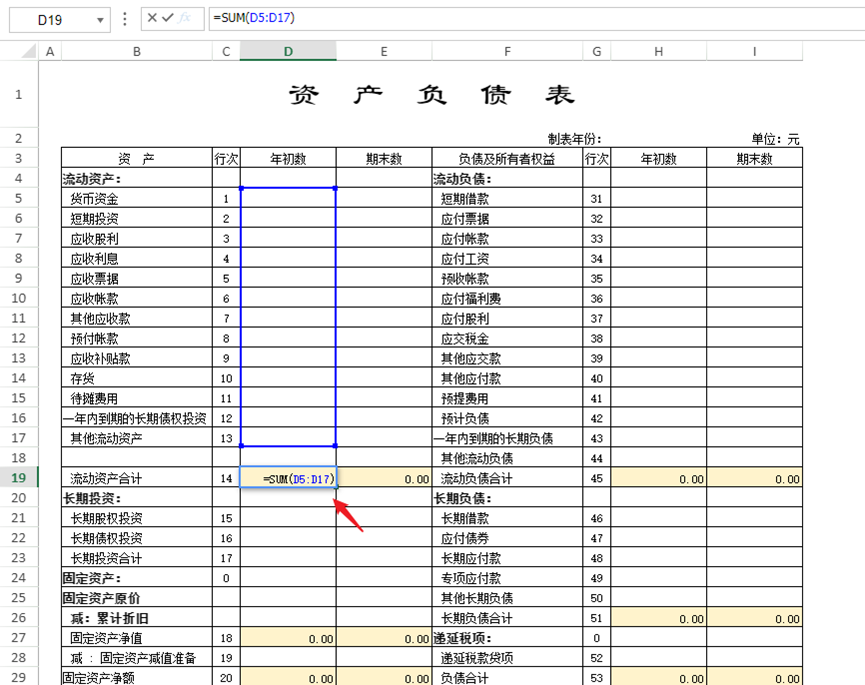
3. 如果是直接填报，在对应科目年初/期末数单元格直接编辑数据就好。在实际业务中，数据往往是由此前的业务逻辑汇总而来的，所以小编准备了一个数据源表，便于后续取数。

数据源：

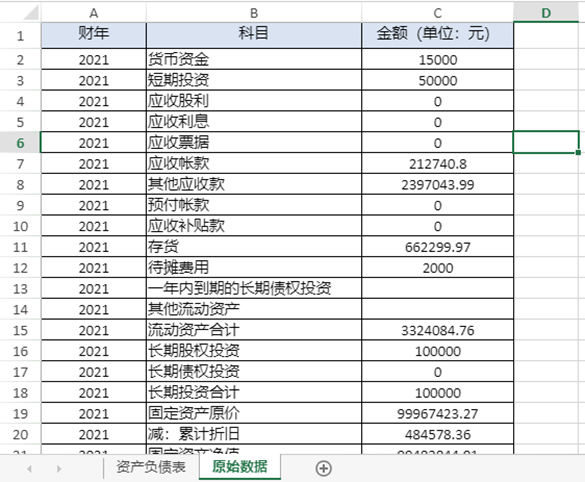
1. 接下来就是将对应数值填写到科目单元格中了，这里我们可以借助 sumifs 公式。关于sumifs 公式的详细介绍可以点击这里查看。以货币资金为例，如果想获取2021年货币资金科目的金额，可以设置下方公式：
   
   

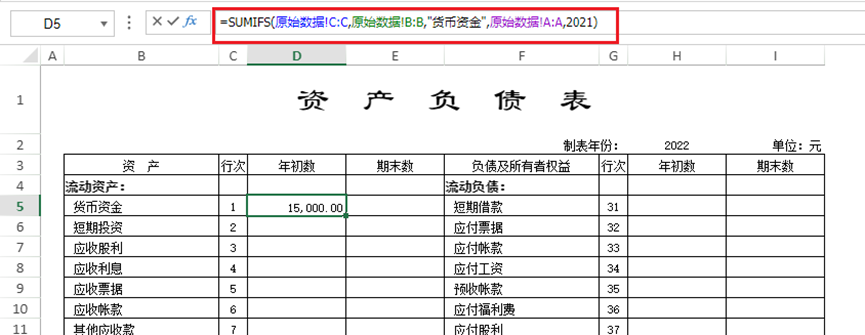
对于填报用户来说，手动选择区域来依次设置公式还是有些繁琐，且如果数据源格式固定，填报用户也无需关注数据区域。所以，可以借助命名信息，进一步将公式简化。

命名信息，即可以给一个单元格、区域、函数，常量，表格定义一个别名，后续可以直接通过这个别名进行引用。

添加的命名信息如下：

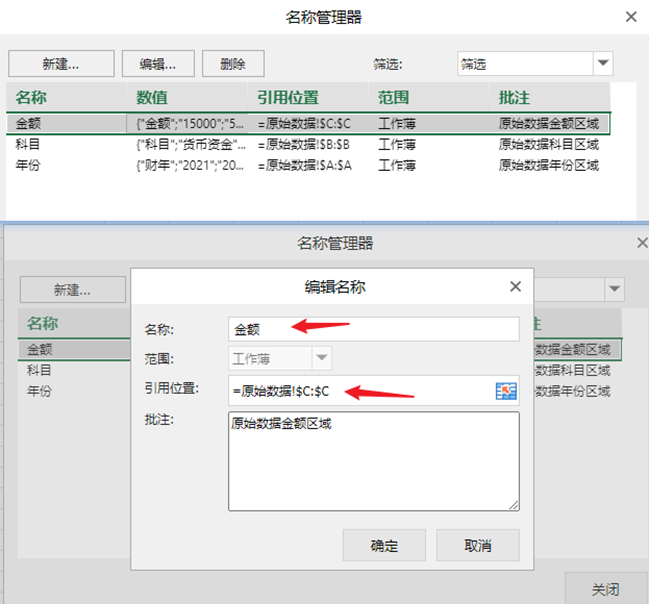
公式可以修改为如下（制表年份-1 即为期初数据对应财年）。

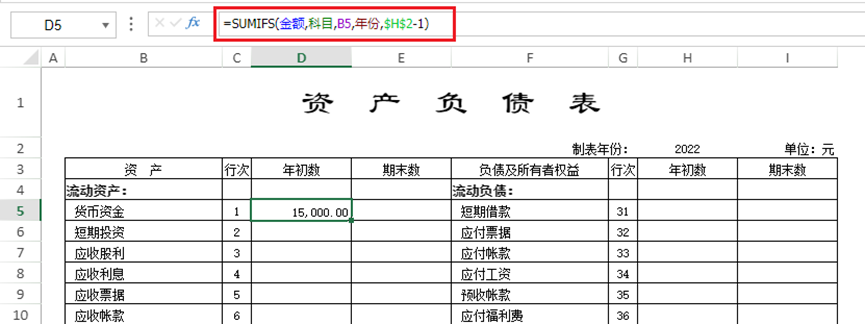
对于期末数，公式为：=SUMIFS(金额，科目,B5,年份,2)

科目值输入完毕后，合计部分公式就可以自动计算了：

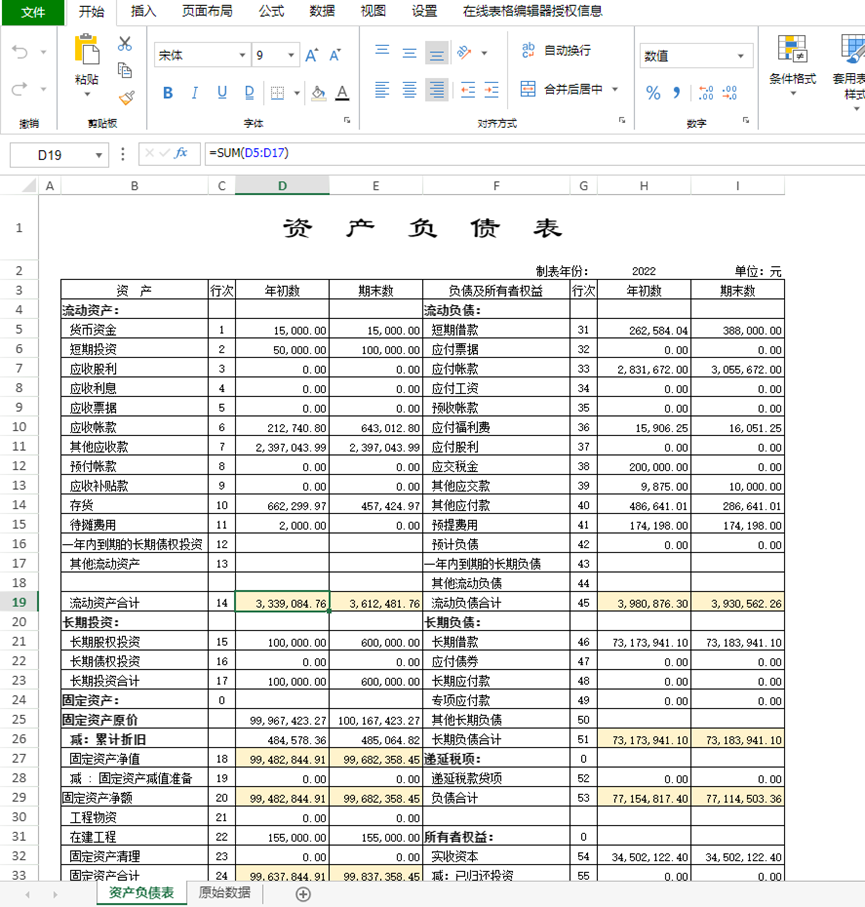
2）权限控制

资产负债表制作完成后，紧接着就进入审批流程了，在数据流转过程中，为了保证数据的完整性和准确性，往往会对编辑权限做一定的限制。比如，审批人只能审阅，无法修改原始数据。原始数据只能由制表者进行修改。这里我们可以结合SpreadJS 表单保护+单元格锁定 功能，实现上述需求。

对于制表者，可以编辑各科目年初数、期末数单元格，因此将其设置为锁定，并开启表单保护。

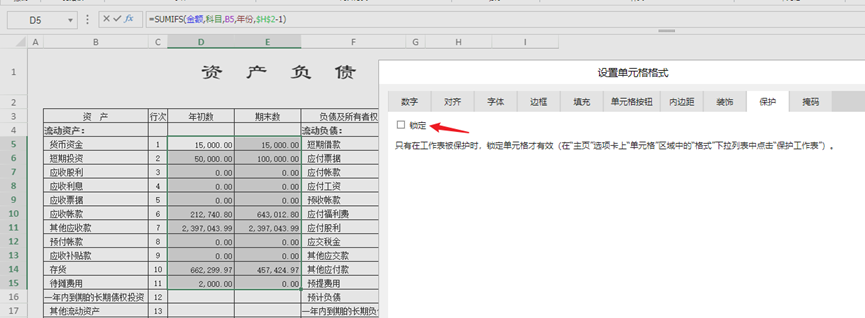
如果尝试修改其他单元格，则会弹窗提示：

当然，这里的弹窗文本也是可以自定制的，更灵活地满足不同项目的风格需求。具体方式可参考下方的教程：https://gcdn.grapecity.com.cn/showtopic-162002-1-1.html

在流转至审批阶段时，审批单元格编辑权限打开，其他单元格处于只读状态，所以可以将B42:E42单元格设置为未锁定，其余单元格设置为锁定。

同样开启表单保护，使编辑限制生效。对于原始数据表单，审批者其实是不关注的，所以可以将此sheet进行隐藏。SpreadJS提供了深度隐藏功能，使用户无法从UI界面进行取消，从而保证了数据的安全性。

填报工作完成后，紧接着就是需要做打印、导出pdf等业务。

3）打印和导出pdf

在打印时，可以直接使用设计器自带的打印功能，点击打印按钮即可唤起浏览器的打印窗口。如果需要调整布局、边距等，可以通过页面布局按钮进行相应设置。

同样地，设计器也提供了类Excel的导出pdf功能。

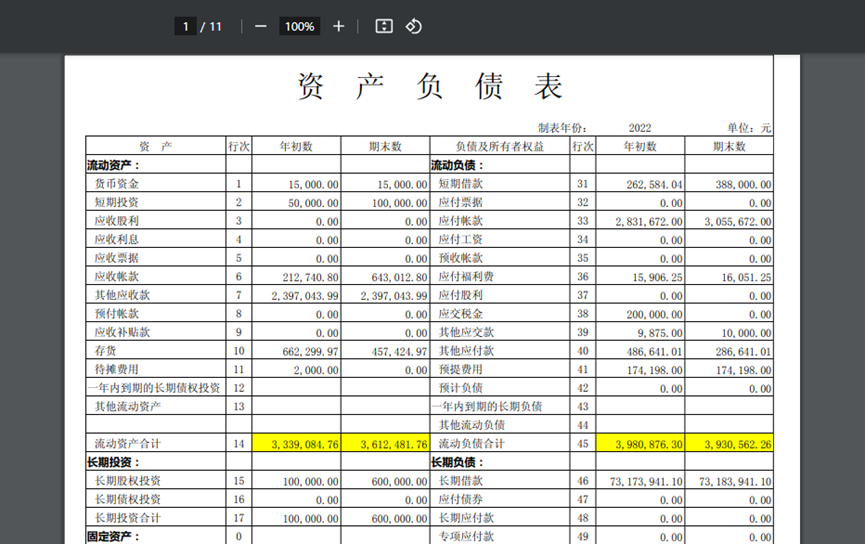
总结

以上就是使用SpreadJS实现一个资产负债表的全过程，如果您想了解更多有关于资产负债表的信息，欢迎点击这里查看。

扩展链接：

【干货放送】财务报表勾稽分析要点，一文读尽！

为什么你的财务报表不出色？推荐你了解这四个设计要点和SpreadJS！

纯前端类 Excel 表格控件在报表勾稽分析领域的应用场景解析