CSP模拟10--总结

今天是我第一次给模拟赛写正规总结--因为今天的题真的受不了了

四道数学题，一点都不拖泥带水的纯血数学题！

T1、黑暗型高松灯

shit

本来是一道放在T4防AK的题，结果学长为了 恶心 锻炼一下我们，直接将T1和T4swap了一下.

一开始看了半个小时挺懵逼的，然后跳了，但心里一直觉得这题能做（起码得拿点暴力分吧），记过后来又跳回来搞了两个小时，但还是啥都没推出来，还耽误了切T2。\(GG\)。

T2、速度型高松灯

\[\huge \color{black}本场考试最大的遗憾
\]

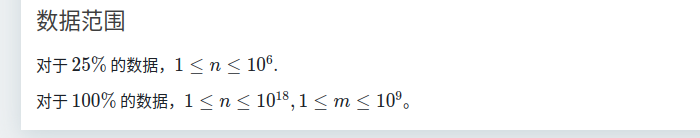
首先一眼有暴力递推式：

\[\large \color{black} f_i = 10^k f_{i-1} + i
\]

是一个n很huge的线性递推，本应该一眼想到矩阵快速幂加速，但是只是在脑子里过了一下，感觉好像行，但是又很不熟悉矩阵快速幂咋打的来着，打了两下，又想起来T1，又想到这是数学专场，是不是别的做法？

总之在不熟悉知识点与不自信的双重影响下，只打了暴力，又跳了。

T4、高松灯

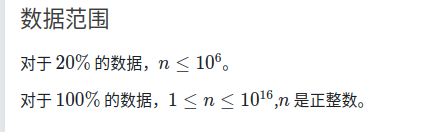
签到题，但我还是挂了10分。

打了个数位DP，结果中间变量写错了，竟然还能有90分。今天状态很差呀。

T3、速度型高松灯

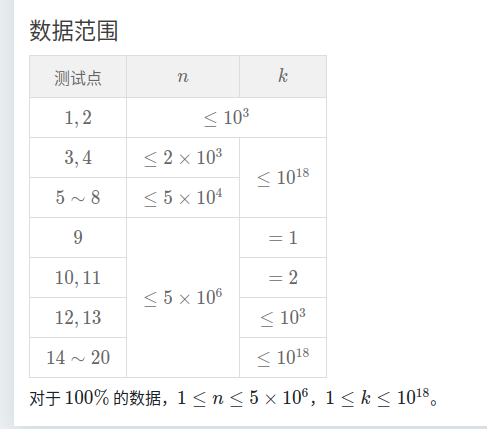
瞪眼莫反，但是考场上根本不会。

恶补莫反。

顺便导一下柿子：

首先替换$ gcd_{i,j} $

$$
\begin{aligned}
&\sum_{i=1}^{n} \sum_{j=1}^{n} (i+j)^k f(d) d\\
=&\sum_{d=1}^{n} \mu^2(d) d \sum_{i=1}^{n} \sum_{j=1}^{n} (i+j)^k [\gcd(i,j)=d]\\
=&\sum_{d=1}^{n} \mu^2(d) d^{k+1} \sum_{i=1}^{\lfloor \frac{n}{d} \rfloor} \sum_{j=1}^{\lfloor \frac{n}{d} \rfloor} (i+j)^k [\gcd(i,j)=1]\\
=&\sum_{d=1}^{n} \mu^2(d) d^{k+1} \sum_{i=1}^{\lfloor \frac{n}{d} \rfloor} \sum_{j=1}^{\lfloor \frac{n}{d} \rfloor} (i+j)^k \sum_{e| \gcd(i,j)} \mu (e)\\
=&\sum_{d=1}^{n} \mu^2(d) d^{k+1} \sum_{e=1}^{n} \mu(e) e^k \sum_{i=1}^{\lfloor \frac{n}{ed} \rfloor} \sum_{j=1}^{\lfloor \frac{n}{ed} \rfloor} (i+j)^k
\end{aligned}
$$
d与e无关，先把$\sum$合并起来变成了：
$$\sum_{d=1}^{n} \sum_{e=1}^{n} e^k d^{k+1} \mu(e) \mu^2 (d) \sum_{i=1}^{\lfloor \frac{n}{ed} \rfloor} \sum_{j=1}^{\lfloor \frac{n}{ed} \rfloor} (i+j)^k $$

设T=ed，S(x)=\(\sum_{i=1}^{x} \sum_{j=1}^{x} (i+j)^k\),我们继续尝试把T提到前面来，变成了：

\[\begin{aligned}
&\sum_{d=1}^{n} \sum_{e=1}^{n} T^k S(\lfloor \frac{n}{T} \rfloor) d \mu(\frac{T}{d}) \mu^2(d)\\
=&\sum_{T=1}^{n} T^k S(\lfloor \frac{n}{T} \rfloor) \sum_{d|T}d \mu (\frac{T}{d}) \mu^2(d)
\end{aligned}
\]

也算是会导一点点的柿子了吧。

\[\]

\[\]

\[\]

\[\Huge \color{salmon}END
\]