c++中的数论知识

写在开头：word的公式打不上来，只能截图了

一.组合数学

(1) 加法定理与乘法原理

1. 加法原理：做一件事情，完成它可以有n类办法，在第一类办法中有m₁种不同的方法，在第二类办法中有m₂种不同的方法，……，在第n类办法中有m_n种不同的方法。那么完成这件事共有N＝m₁＋m₂＋…＋m_n种不同的方法。
2. 乘法原理：做一件事情，完成它需要分成n个步骤，做第一步有m₁种不同的方法，做第二步有m₂种不同的方法，……，做第n步有种m_n不同的方法，那么完成这件事有N＝m₁m₂…m_n种不同的方法。
3. 两个原理的区别：一个与分类有关，一个与分步有关；加法原理是“分类完成”，乘法原理是“分步完成”

(2) 排列与组合

1. 排列

概念：从n个不同元素中，任取m(m≤n)个元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列。

排列数：从n个不同元素中取出m(m≤n)个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号表示。

计算公式：＝n(n－1)(n－2)……(n－m＋1)＝

2.组合

概念：从n个不同元素中，任取m(m≤n)个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合。

组合数：从n个不同元素中取出m(m≤n)个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数，用符号表示。

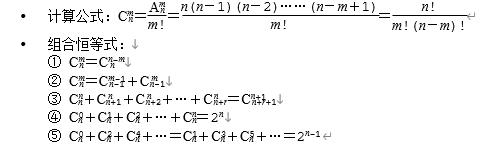
(3) 鸽巢原理（抽屉原理）

1. 简单形式：如果n＋1个物体被放进n个盒子，那么至少有一个盒子包含两个或更多的物体。
2. 加强形式：令q₁，q₂，…，q_n为正整数。如果将q₁＋q₂＋…＋q_n－n＋1个物体放入n个盒子内，那么或者第一个盒子至少含有q₁个物体，或者第二个盒子至少含有q₂个物体，…，或者第n个盒子含有q_n个物体

　　

(4) 容斥原理

1. 集S的不具有性质P₁，P₂，…，P_m的物体的个数
   
   |A₁∩A₂∩…∩A_m|＝|S|－∑|A_i|＋∑|A_i∩A_j|－∑|A_i∩A_j∩A_k|＋…＋(－1)^m|A₁∩A₂∩…∩A_m|
2. 推论：至少具有性质P₁，P₂，...P_m之一的集合S的物体的个数有
   
   |A₁∪A₂∪…∪A_m|＝|S|—|A₁∩A₂∩…∩A_m|＝
   
   ∑|A_i|－∑|A_i∩A_j|＋∑|A_i∩A_j∩A_k|＋…＋(－1)^m+1|A₁∩A₂∩…∩A_m|

二.同余的性质

三.最大公约数，最小公约数

四.解不定方程

五.同余方程

六.素数和素数表

七.分解质因数