并查集（UnionFind）

并查集和其他树形结构不一样，是由孩子指向父亲，它解决了一些连接问题，怎么才能确定两个点是否相连呢？并查集可以非常快的确定两个点是否连接。

如何确定连个点是否连接呢？

我们可以用一个数组表示，对于0到9每个不同的编号可以表示不同的对象，这里可以看作一个点，而编号对应的不同的元素可以表示不同的集合，其中[0，2，4，6，8]表示一个集合。这样就可以表示连接问题了，0和2就是表示相连接，因为它们在一个集合，0和1因不在一个集合所以不连接。

对于一组数据并查集主要支持两个动作：

• isConnected(p,q)：查询元素p和q是否在一个集合
• unionElements(p,q)：合并元素p和q的集合

Code

#pragma once

class UF {
private:
    virtual const int getSize() const noexcept = 0;

    virtual bool isConnected(int p, int q) = 0;

    virtual void unionElements(int p, int q) = 0;
};

#pragma once

#include "UF.h"
#include<cassert>

class UnionFind1 : public UF {
private:
    int *id;
    int size;
public:
    UnionFind1(int capacity) {
        id = new int[capacity];
        size = capacity;
        for (int i = 0; i < size; ++i) {
            id[i] = i;  //初始化不同的元素表示不同的集合都不相连
        }
    }

    const int getSize() const noexcept {
        return size;
    }
    //返回p所在的集合
    int find(int p) {
        assert(p >= 0 && p < size);
        return id[p];
    }
    //判断是否相连
    bool isConnected(int p, int q) {
        return find(p) == find(q);
    }
    //合并集合
    void unionElements(int p, int q) {
        int pID = find(p);
        int qID = find(q);
        if (pID == qID) {
            return;
        }

        for (int i = 0; i < size; ++i) {
            if (id[i] == pID) {
                id[i] = qID;    //让两个集合都相同就行了
            }
        }
    }
};

优化unionElements

从代码中可以看到：

• unionElements的时间复杂度是O(n)
• isConnected的时间复杂度是O(1)

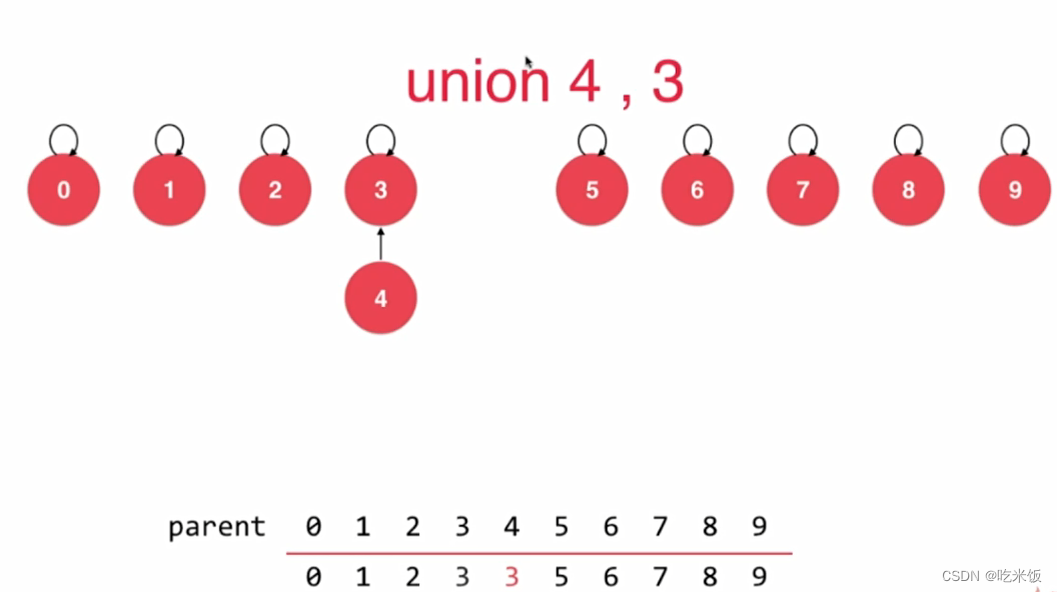
将每个元素，看做是一个节点，每个节点指向它的父节点，而根节点指向自己。如果我们进行unionElements(4,3)操作，那么就是让4索引的元素为3。同在一个树下面就是同一个集合表示相连。

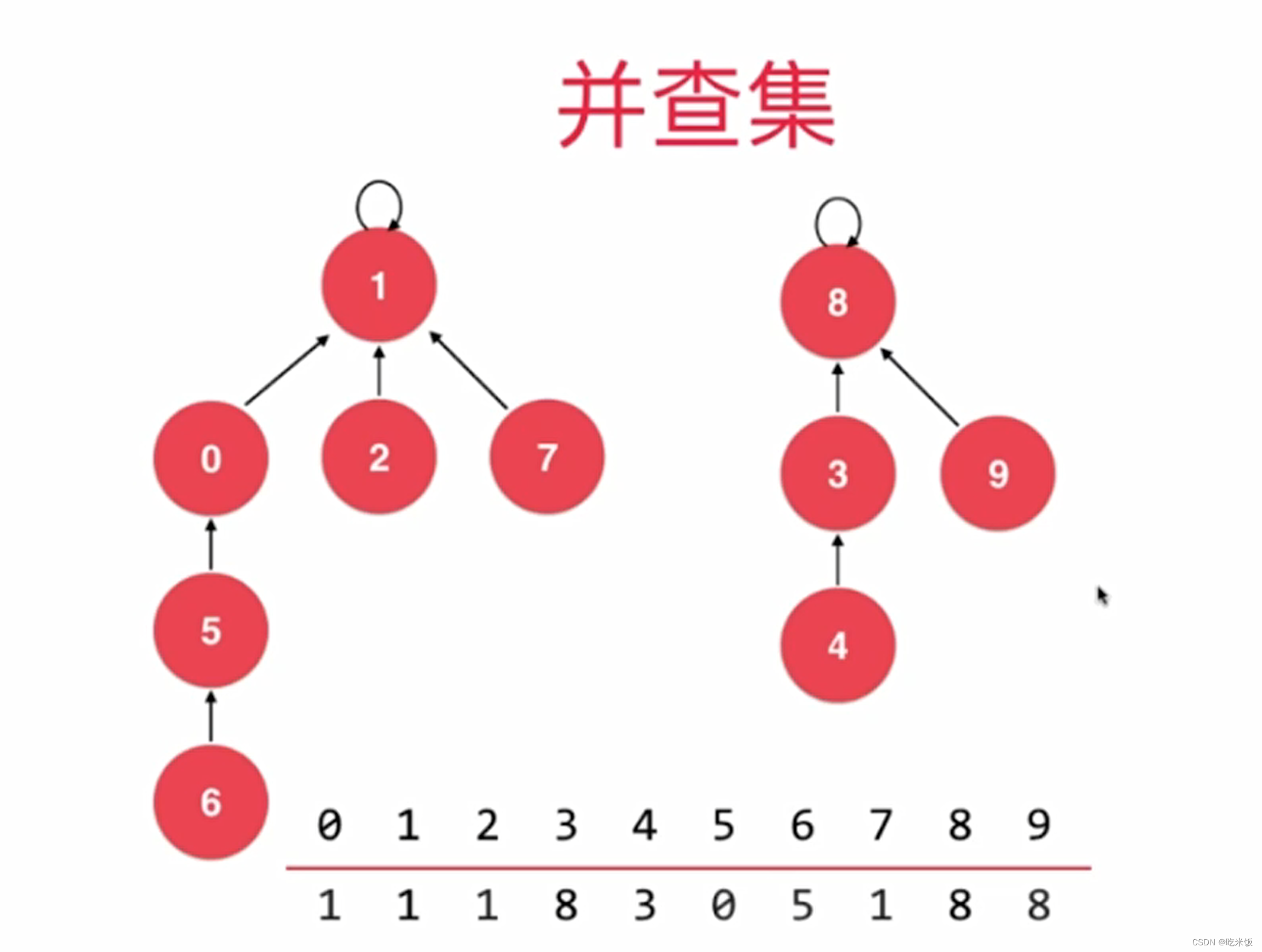
Code

#pragma once

#include "UF.h"
#include<cassert>

class UnionFind2 : public UF {
private:
    int *parent;
    int size;
public:
    UnionFind2(int capacity) {
        parent = new int[capacity];
        size = capacity;
        for (int i = 0; i < size; ++i) {
            parent[i] = i;
        }
    }

    const int getSize() const noexcept {
        return size;
    }

    int find(int p) {
        assert(p >= 0 && p < size);
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }

    bool isConnected(int p, int q) {
        return find(p) == find(q);
    }

    void unionElements(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);

        if (pRoot == qRoot) {
            return;
        }
        parent[pRoot] = qRoot;
    }
};

基于size的优化

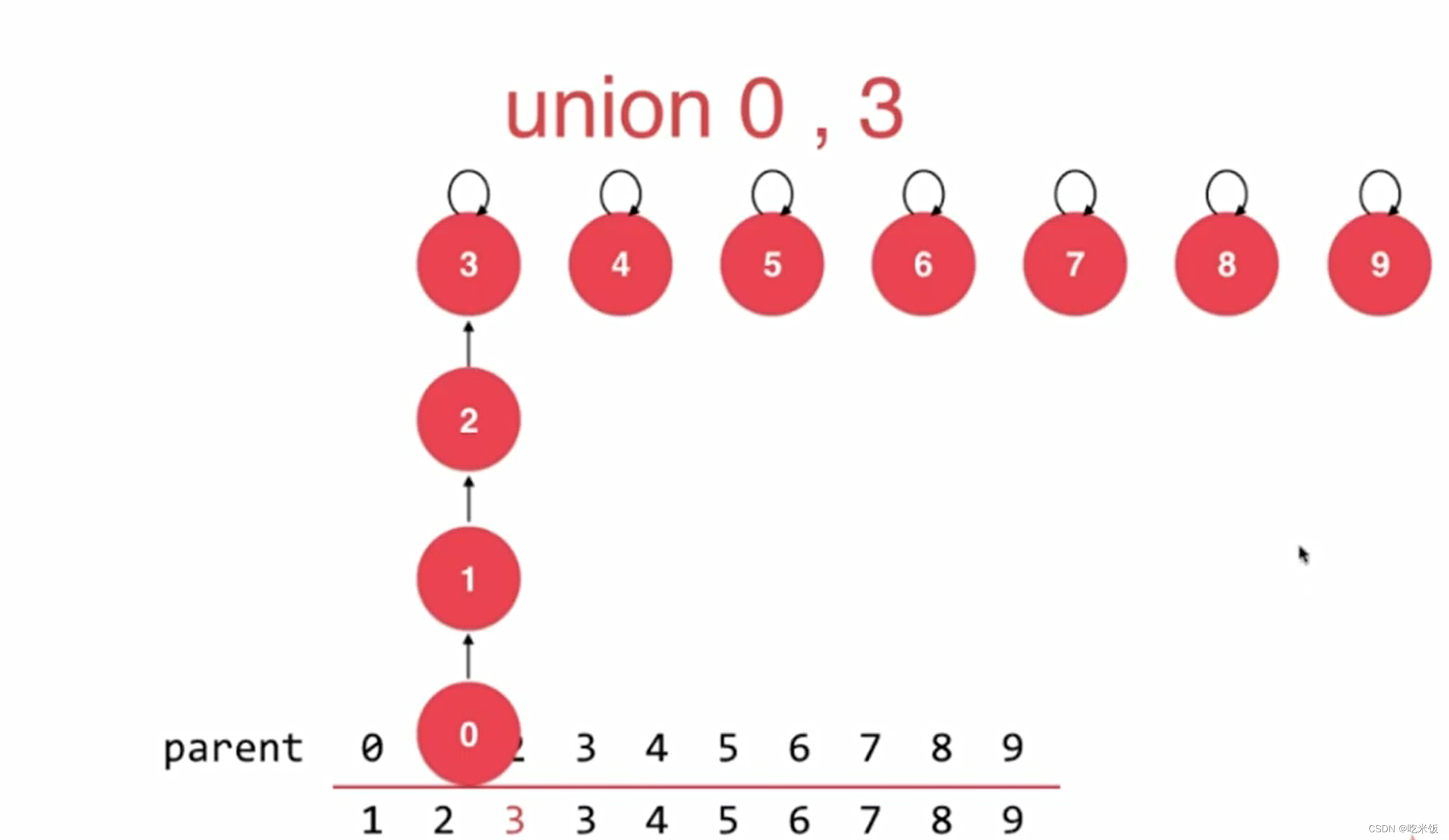
由于对真正合并那两个元素所在树的形状没有做判断，很多时候会增加树的高度。

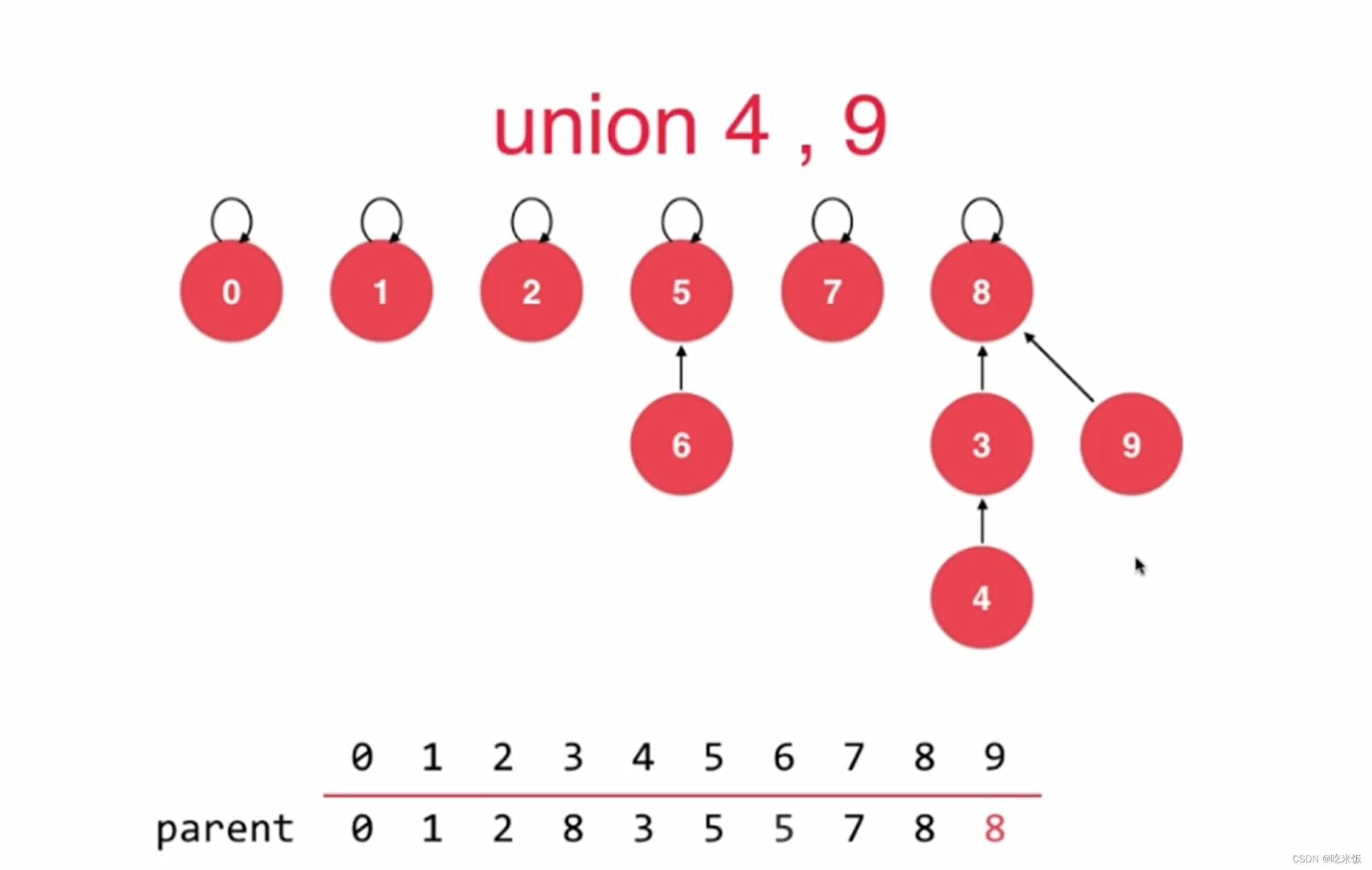
优化方法：节点个数小的那个节点去指向节点个数多个那个根节点。

Code

#ifndef UNION_FIND_UNIONFIND3_H
#define UNION_FIND_UNIONFIND3_H

#include "UF.h"
#include <cassert>

class UnionFind3 : public UF {
private:
    int *parent;
    int *sz;
    int size;
public:
    UnionFind3(int capacity) {
        parent = new int[capacity];
        sz = new int[capacity];
        size = capacity;
        for (int i = 0; i < size; ++i) {
            parent[i] = i;
            sz[i] = 1;
        }
    }

    int getSize() {
        return size;
    }

    int find(int p) {
        assert(p >= 0 && p < size);
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }

    bool isConnected(int p, int q) {
        return find(p) == find(q);
    }

    void unionElements(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);

        if (pRoot == qRoot) {
            return;
        }

        if (sz[pRoot] < sz[qRoot]) {
            parent[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        } else {
            parent[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }
    }
};
#endif //UNION_FIND_UNIONFIND3_H

基于rank的和优化

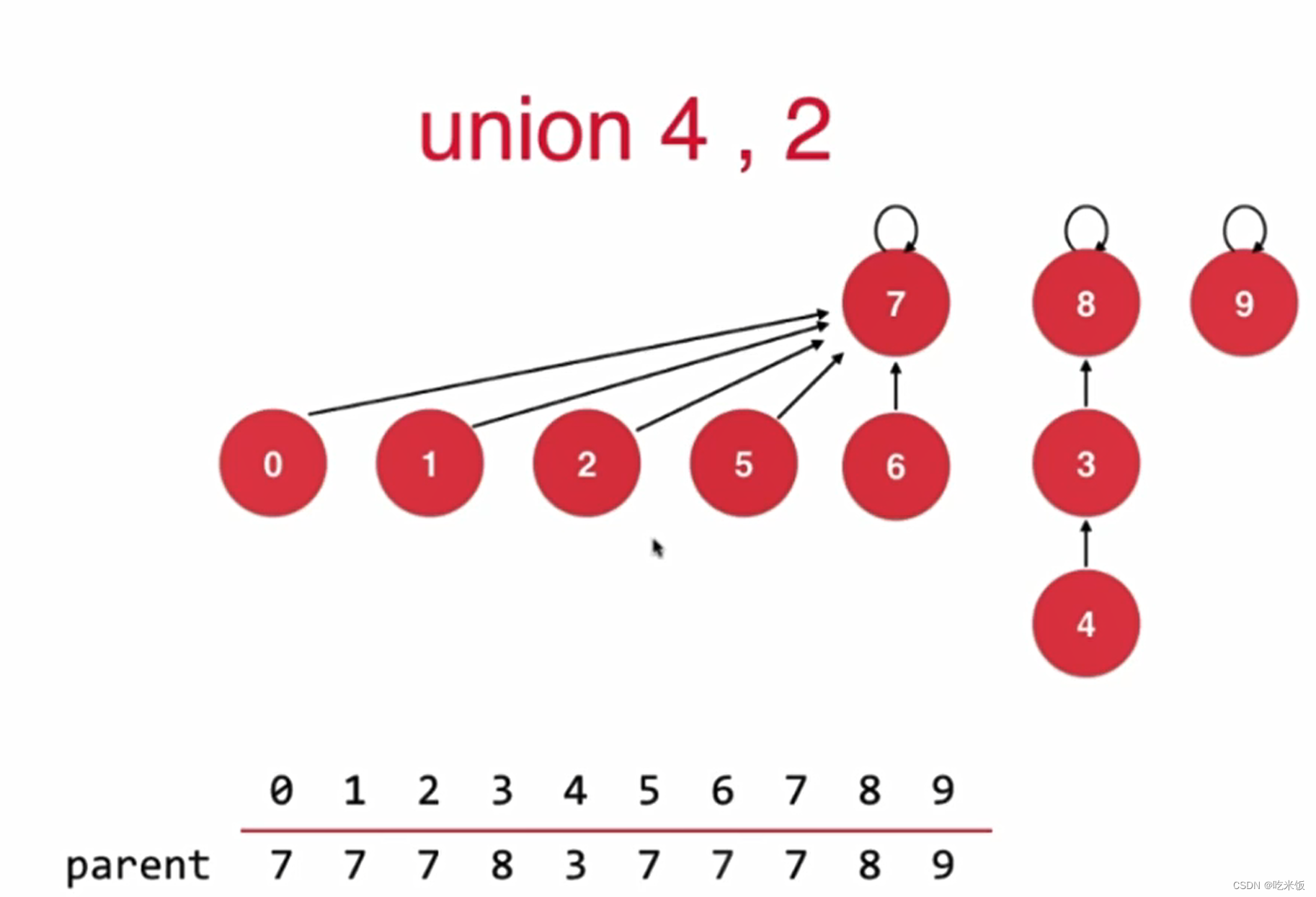
如果基于size优化会增加树的高度



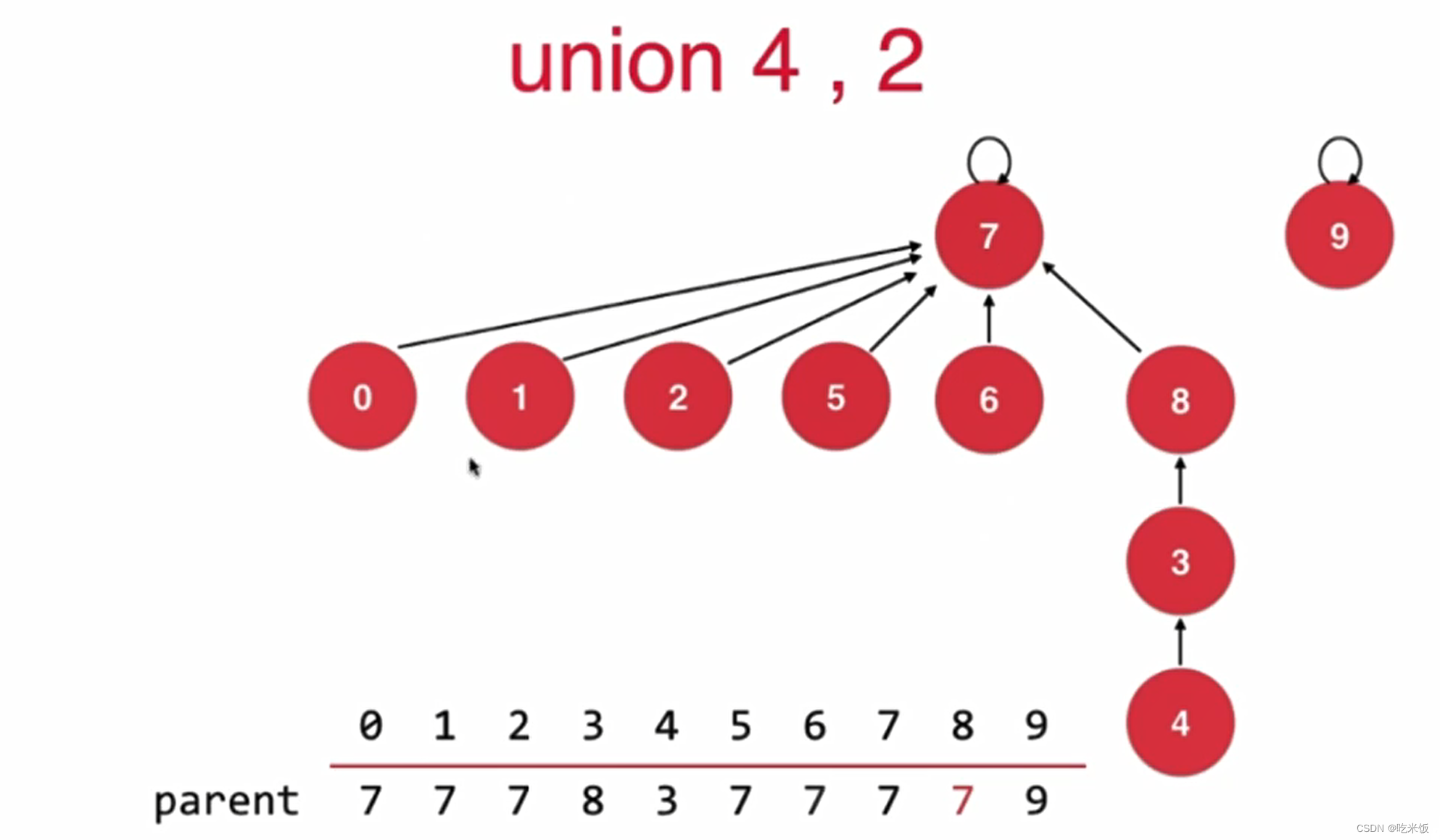
如果基于rank的优化rank[i]表示根节点为i的树的高度

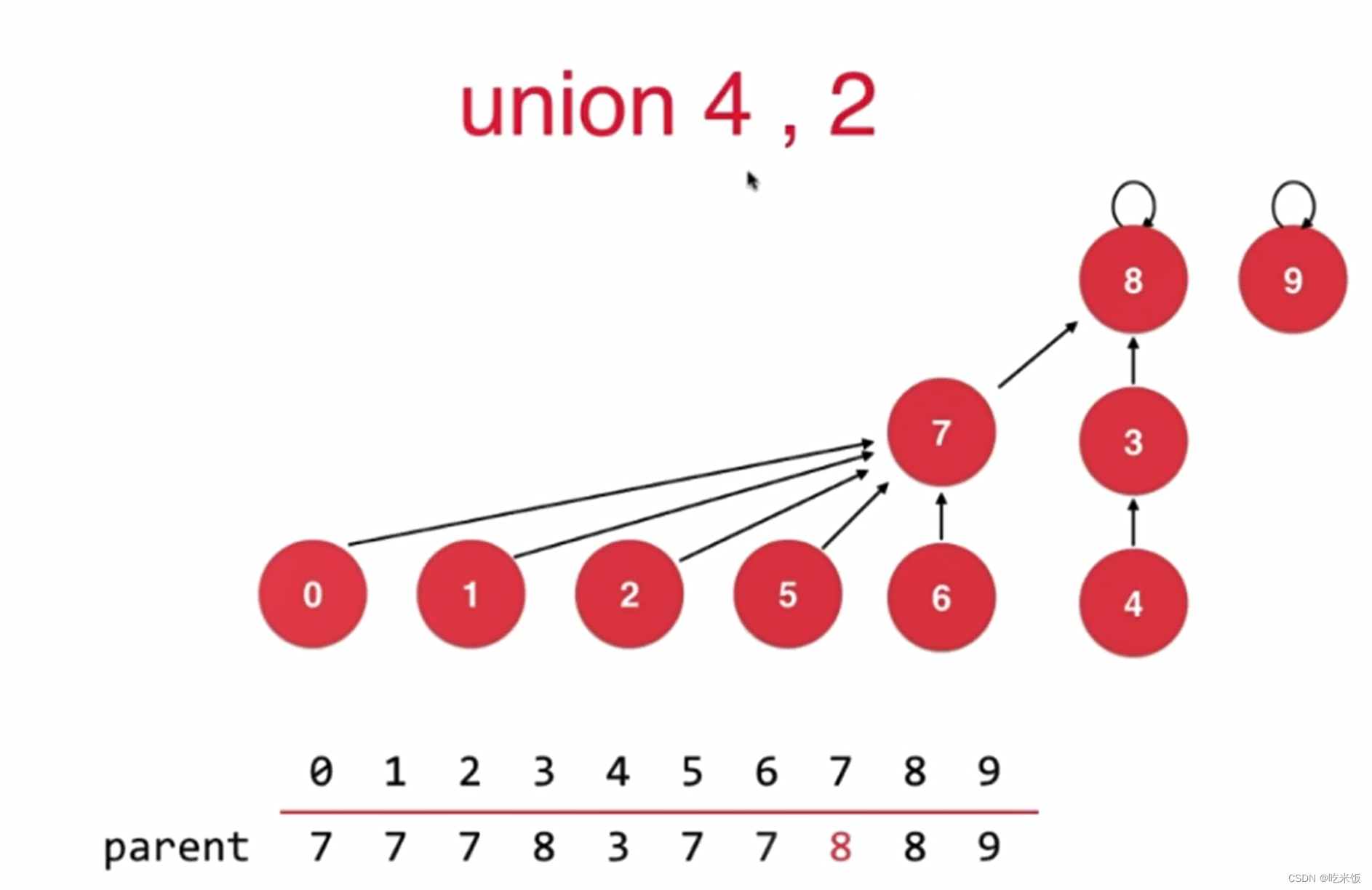
Code

#ifndef UNION_FIND_UNIONFIND4_H
#define UNION_FIND_UNIONFIND4_H

#include "UF.h"
#include <cassert>

class UnionFind4 : public UF {
private:
    int *parent;
    int *rank;
    int size;
public:
    UnionFind4(int capacity) {
        parent = new int[capacity];
        rank = new int[capacity];
        size = capacity;
        for (int i = 0; i < size; ++i) {
            parent[i] = i;
            rank[i] = 1;
        }
    }

    int getSize() {
        return size;
    }

    int find(int p) {
        assert(p >= 0 && p < size);
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }

    bool isConnected(int p, int q) {
        return find(p) == find(q);
    }

    void unionElements(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);

        if (pRoot == qRoot) {
            return;
        }

        if (rank[pRoot] < rank[qRoot]) {
            parent[pRoot] = qRoot;
        } else if (rank[pRoot] > rank[qRoot]) {
            parent[qRoot] = pRoot;
        } else {
            parent[qRoot] = pRoot;
            rank[pRoot] += 1;
        }
    }
};
#endif //UNION_FIND_UNIONFIND4_H

路径压缩

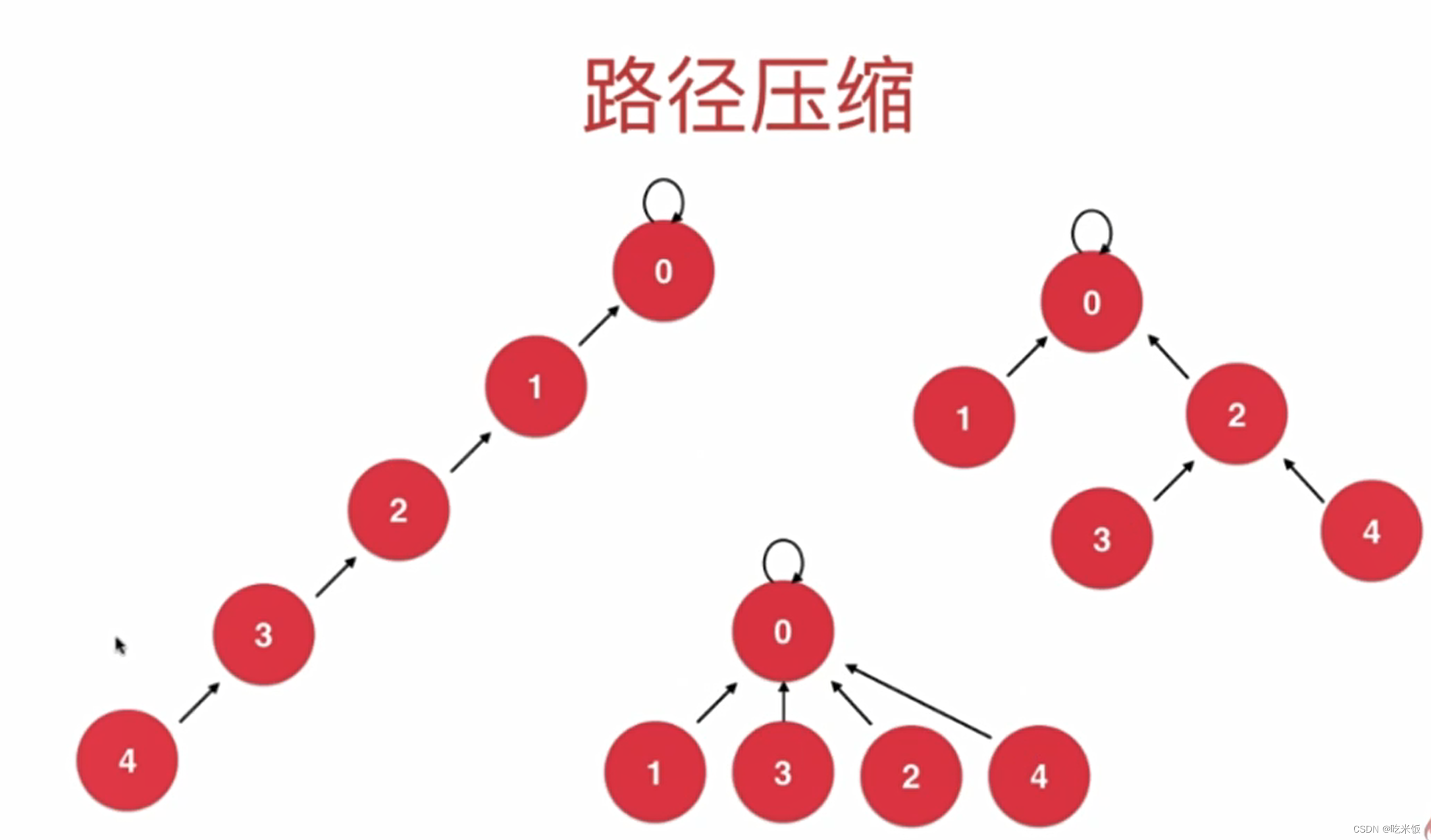
优化方法一

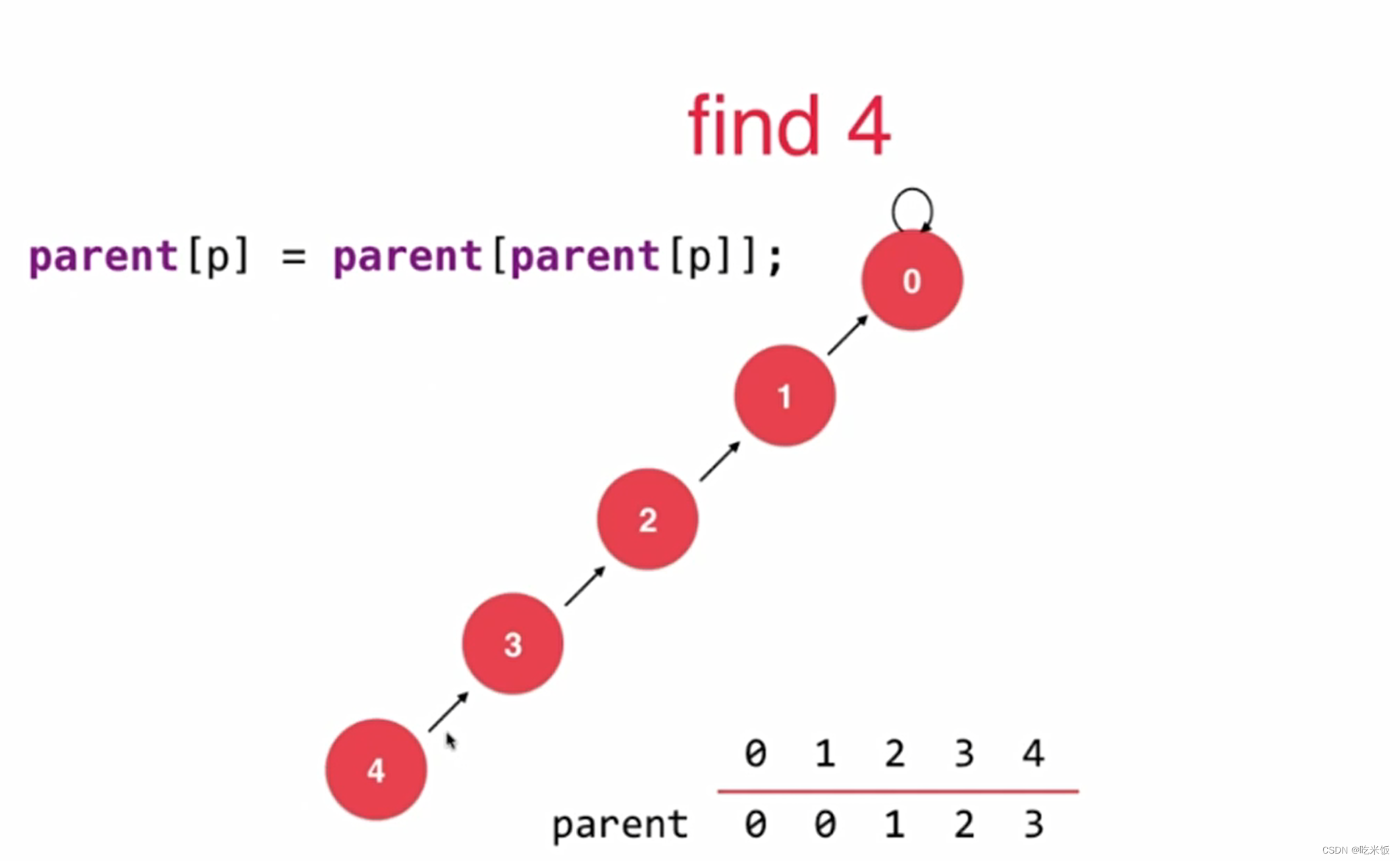
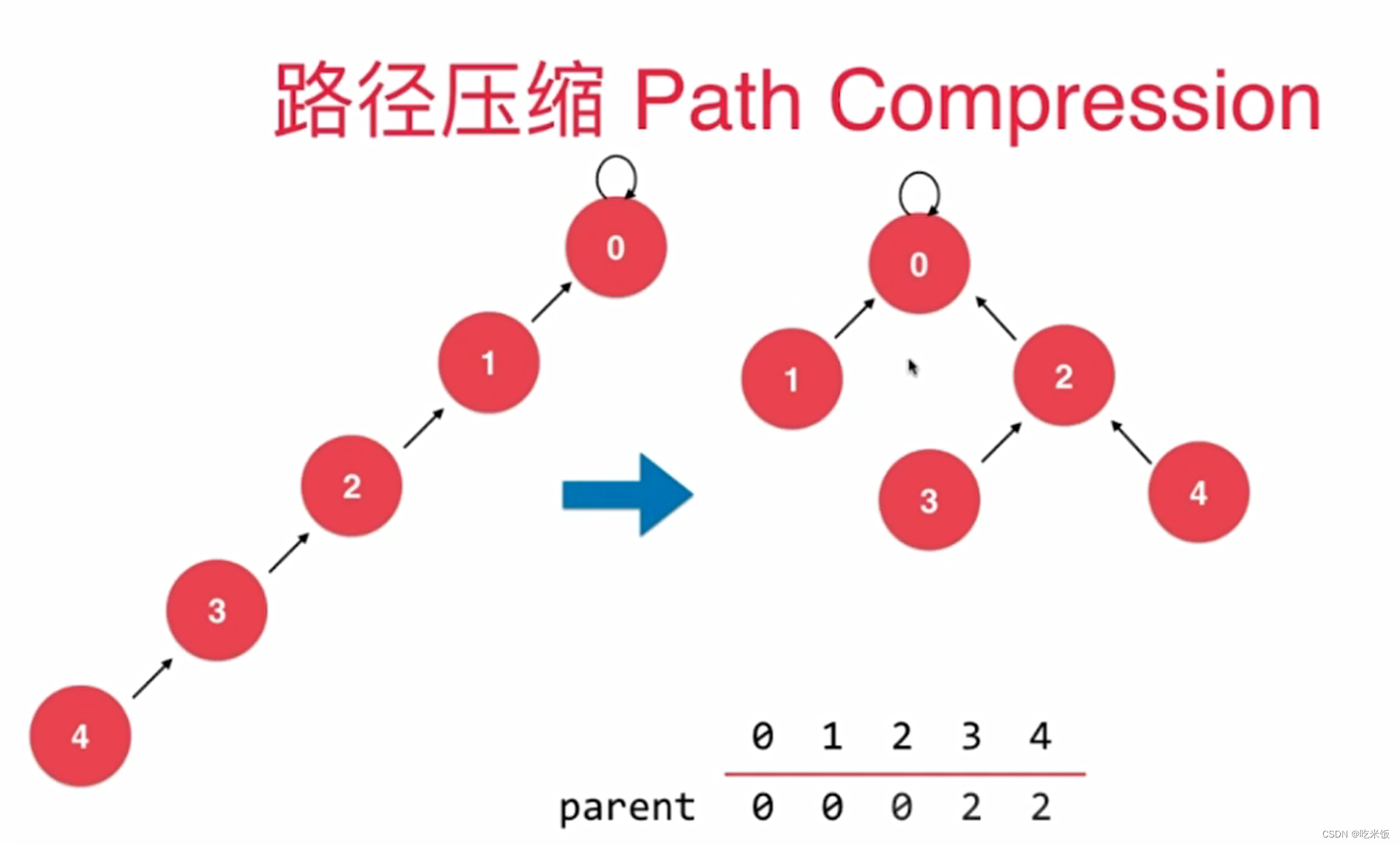
优化方法二

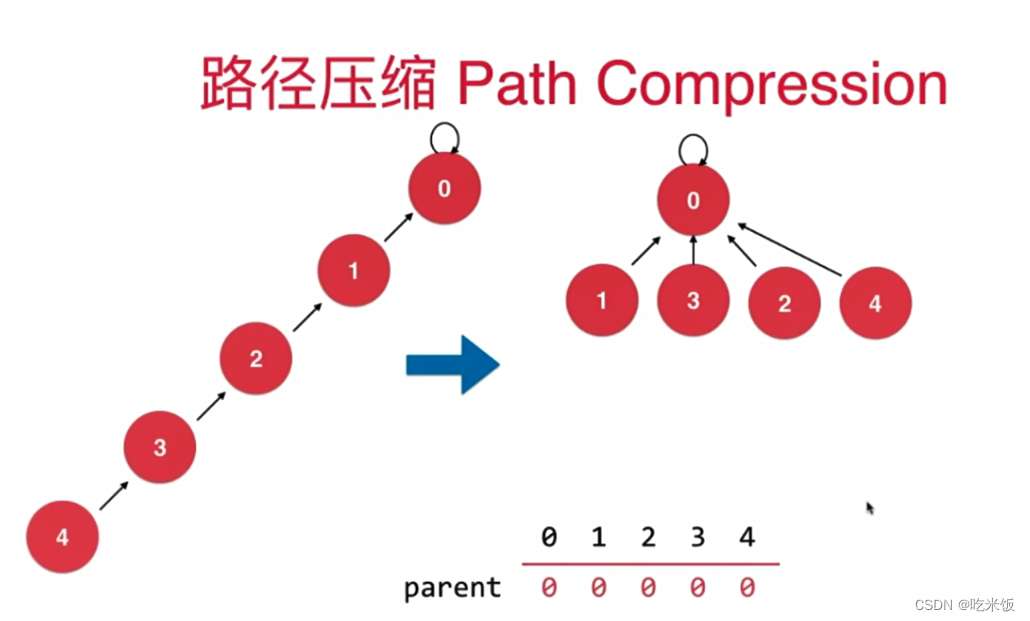
Code

#pragma once

#include "UF.h"
#include<cassert>

class UnionFind : public UF {
public:
    UnionFind(int cap) : size(cap) {
        parent = new int[size];
        rank = new int[size];
        for (int i = 0; i < size; ++i) {
            parent[i] = i;
            rank[i] = 1;
        }
    }

    ~UnionFind() noexcept {
        delete[] parent;
        parent = nullptr;
    }

    const int getSize() const noexcept override {
        return size;
    }

    //查询元素p和q是否在一个集合
    bool isConnected(int p, int q) override {
        return find(p) == find(q);
    }

    //合并元素p和q的集合
    void unionElements(int p, int q) override {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot) {
            return;
        }
        //就把其中一个的根节点挂到另一个的根上
        if (rank[pRoot] < rank[qRoot]) {
            parent[pRoot] = qRoot;  //高度小的根节点指向高度大的根节点，从而减少树的高度，防止退化
        } else if (rank[qRoot] < rank[pRoot]) {
            parent[qRoot] = pRoot;
        } else {
            parent[qRoot] = pRoot;
            ++rank[pRoot];
        }
    }

private:
    //查找元素p对应的集合编号，O(h)复杂度, h为树的高度
    //根节点就是集合编号，且根节点指向自己，索引 p == parent[p]
    int find(int p) {
        assert(p >= 0 && p < size);
        while (p != parent[p]) {
            parent[p] = parent[parent[p]];  //路径压缩，让p这个节点指向它父亲的父亲
            p = parent[p];
        }
        return p;
    }
    //递归版路径压缩，让集合中所有节点指向根节点
    int recFind(int p) {
        assert(p >= 0 && p < size);
        if (p != parent[p]) {
            parent[p] = find(parent[p]);
        }
        return parent[p];
    }

private:
    int *parent;
    int *rank;
    int size;
};