LeetCode 栈与队列篇（12、155、84、239）

20. 有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。

左括号必须以正确的顺序闭合。

注意空字符串可被认为是有效字符串。

示例 1:

输入: "()"

输出: true

示例 2:

输入: "()[]{}"

输出: true

示例 3:

输入: "(]"

输出: false

示例 4:

输入: "([)]"

输出: false

示例 5:

输入: "{[]}"

输出: true

solution1 往stack放右括号

class Solution {
    public boolean isValid(String s) {
        //整一个栈
        Stack<Character> stack = new Stack<Character>();
        for (char c : s.toCharArray()) {
            if (c == '{') stack.push('}');
            else if (c == '[') stack.push(']');
            else if (c == '(') stack.push(')');
            else if (stack.isEmpty() || stack.pop() != c) return false;
        }
        return stack.isEmpty();
    }
}

solution2 往stack放左括号

class Solution {
    public boolean isValid(String s) {
        if (s.length() == 0) return true;
        if ((s.length() & 1) == 1) return false;
        Stack<Character> stack = new Stack<>();
        Map<Character,Character> map = new HashMap<>();
        map.put(')','(');
        map.put(']','[');
        map.put('}','{');
        for (int i = 0 ;i < s.length();i++) {
            char c = s.charAt(i);
            if (c == '(' || c == '[' || c == '{'){
                stack.push(c);
            }else{
                if (stack.size() == 0 || map.get(c) != stack.pop()) {
                    return false;
                }
            }
        }
        return stack.isEmpty();

    }
}

solution3 暴力解法，遍历数组，有对称消掉并继续，没对称结束

class Solution {
    // private static final Map<Character,Character> = new HashMap<>()
    public boolean isValid(String s) {
        if (s.length() == 0) return true; //空
        if ((s.length() & 1) == 1) return false; // 奇数、位运算
        int length;
        do{
            length = s.length();
            s = s.replace("()","").replace("[]","").replace("{}","");
        }while(length!=s.length());
        return s.length() == 0;
    }
}

solution4 字符串加递归

class Solution {
    public boolean isValid(String s) {
        if (s.contains("()") || s.contains("[]") || s.contains("{}")) {
            return isValid(s.replace("()","").replace("[]","").replace("{}",""));
        }else {
            return "".equals(s);
        }
    }
}

155. 最小栈

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

push(x) —— 将元素 x 推入栈中。

pop() —— 删除栈顶的元素。

top() —— 获取栈顶元素。

getMin() —— 检索栈中的最小元素。

示例:

输入：

["MinStack","push","push","push","getMin","pop","top","getMin"]

[[],[-2],[0],[-3],[],[],[],[]]

输出：

[null,null,null,null,-3,null,0,-2]

解释：

MinStack minStack = new MinStack();

minStack.push(-2);

minStack.push(0);

minStack.push(-3);

minStack.getMin(); --> 返回 -3.

minStack.pop();

minStack.top(); --> 返回 0.

minStack.getMin(); --> 返回 -2.

提示：

pop、top 和 getMin 操作总是在 非空栈 上调用。

solution1

//整两个栈
class MinStack {
    Stack<Integer> stack;
    Stack<Integer> minStack;
    public MinStack() {
        stack = new Stack<>();
        minStack = new Stack<>();
    }

    public void push(int x) {
        stack.push(x);
        if (minStack.isEmpty() || x <= minStack.peek()) minStack.push(x);
    }

    public void pop() {
        if (stack.pop().equals(minStack.peek())) minStack.pop();
    }

    public int top() {
        return stack.peek();
    }

    public int getMin() {
        return minStack.peek();
    }
}

solution2

//一个栈
class MinStack {
    Stack<Integer> stack;
    Integer i;
    public MinStack() {
        stack = new Stack<>();
    }

    public void push(int x) {
        if (i != null && x <= i) {
            stack.push(i);
            i = x;
        }
        if (i == null) i = x;
        stack.push(x);
    }

    public void pop() {
        if (stack.pop().equals(i) && !stack.isEmpty()) {
            i = stack.pop();
        }
        if (stack.isEmpty()) i = null;
    }

    public int top() {
        return stack.peek();
    }

    public int getMin() {
        return i;
    }
}

class MinStack {
    int min = Integer.MAX_VALUE;
    Stack<Integer> stack = new Stack<Integer>();
    public void push(int x) {
        //当前值更小
        if(x <= min){
            //将之前的最小值保存
            stack.push(min);
            //更新最小值
            min=x;
        }
        stack.push(x);
    }

    public void pop() {
        //如果弹出的值是最小值，那么将下一个元素更新为最小值
        if(stack.pop() == min) {
            min=stack.pop();
        }
    }

    public int top() {
        return stack.peek();
    }

    public int getMin() {
        return min;
    }
}

solution3

//存差值
class MinStack {
     Stack<Long> stack;
     long i;
    /** initialize your data structure here. */
    public MinStack() {
        stack = new Stack<>();
    }

    public void push(int x) {
        if (stack.isEmpty()){
            i = x;
            stack.push(x-i);
        }else {
            if (x < i) {
                stack.push(x-i);
                i = x;
            }else{
                stack.push(x-i);
            }

        }
    }

    public void pop() {
        Long pop = stack.pop();
        //弹出后恢复上一个最小值
        if ( pop < 0 ) {
            i = i - pop;
        }

    }

    public int top() {
        long top = stack.peek();
        if (top < 0) {
            return (int)i;
        }else{
            return (int)(top + i);
        }
    }

    public int getMin() {
        return (int)i;
    }
}

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

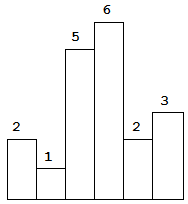
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。



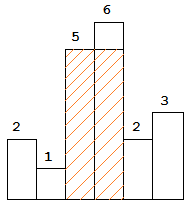
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]

输出: 10

solution1

//暴力解法1
//时间复杂度为（n^3）Java 超时
class Solution {
    public int largestRectangleArea(int[] heights) {
        if (heights == null || heights.length == 0) return 0;
        int max = heights[0];
        for (int i = 0; i < heights.length; i ++) {
            for (int j = i; j < heights.length; j ++) {
                  //每两个之间的最小值为高
                int min = heights[j];
                for (int k = i;k <= j; k++){
                    min = Math.min(min,heights[k]);
                    max = Math.max(max,min*(k-i+1));
                }
            }
        }
        return max;
    }
}

solution2

//暴力2，以每个柱子为最低点,找到对应的矩形
//时间复杂度为（n^2）
class Solution {
    public int largestRectangleArea(int[] heights) {
        if (heights == null || heights.length == 0) return 0;
        int max = 0;
        for (int i = 0; i < heights.length; i ++) {
            //遍历左边，找是否有比本身大的
            int left = i;
            while (left > 0 && heights[left-1] >= heights[i]){
                left --;
            }
            //遍历右边，找是否有比本身小的
            int right = i;
            while (right < heights.length - 1 && heights[right+1] >= heights[i]) {
                right ++;
            }
            max = Math.max((right - left + 1)*heights[i],max);
        }
        return max;
    }
}

solution3

// 时间、空间复杂度均为O(n)
// 每个的左右边界为比它小的值，栈从小到大放，可以保证左边界，遇到比它小的为右边界，即可计算矩形面积
class Solution {
    public int largestRectangleArea(int[] heights) {
        if (heights == null || heights.length == 0) return 0;
        Stack<Integer> stack = new Stack<>();
        stack.push(-1);
        int max = 0;
        //按从小到大插入栈，确保每个插入的值知道它的左边界，遇到比它小的即确定右边界
        for (int i = 0; i < heights.length; i ++) {
            while (stack.peek() != -1 && heights[stack.peek()] >= heights[i]) {
                max = Math.max(max,heights[stack.pop()] * (i - stack.peek() - 1));
                // 确定了左右边界，右边界为比它小的，左边界为栈里比它小的后一位
            }
            stack.push(i);
        }
        //清空栈
        while (stack.peek() != -1)
            max = Math.max(max, heights[stack.pop()] * (heights.length - stack.peek() - 1));
        return max;
    }
}

solution4

//用两个数组
class Solution {
    public int largestRectangleArea(int[] heights) {
        if (heights == null || heights.length == 0) {
            return 0;
        }
        //整两个数组记录每个数的左右边界，即从左算和右算的最小值
        int[] lessFromLeft = new int[heights.length];
        int[] lessFromRight = new int[heights.length];
        lessFromRight[heights.length - 1] = heights.length;
        lessFromLeft [0] = -1;
        // 确定左边界
        for (int i = 1;i < heights.length; i++){
            int p = i-1;
            while (p >= 0 && heights[p] >= heights[i]) {
                p = lessFromLeft[p];
            }
            lessFromLeft[i] = p;
        }
        //确定右边界
        for (int i = heights.length - 2;i >= 0;i --){
            int p = i + 1;
            while(p < heights.length && heights[p] >= heights[i]){
                p = lessFromRight[p];
            }
            lessFromRight[i] = p;
        }
        int max = 0;
        for (int i = 0; i < heights.length; i ++){
            max = Math.max(max,(lessFromRight[i]-lessFromLeft[i]-1)*heights[i]);
        }
        return max;

    }
}

239. 滑动窗口最大值

给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

进阶：

你能在线性时间复杂度内解决此题吗？

示例:

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3

输出: [3,3,5,5,6,7]

解释:

滑动窗口的位置 最大值

---

[1 3 -1] -3 5 3 6 7 3

1 [3 -1 -3] 5 3 6 7 3

1 3 [-1 -3 5] 3 6 7 5

1 3 -1 [-3 5 3] 6 7 5

1 3 -1 -3 [5 3 6] 7 6

1 3 -1 -3 5 [3 6 7] 7

提示：

1 <= nums.length <= 10^5

-10^4 <= nums[i] <= 10^4

1 <= k <= nums.length

solution1 暴力法

//时间复杂度为O(nk)，Java代码无法通过
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int[] result = new int[nums.length-k+1];
        for (int i = 0;i < nums.length-k+1;i ++) {
            int max = Integer.MIN_VALUE;
            for (int j = i;j < i+k;j++) {
                max = Math.max(max,nums[j]);
            }
            result[i] = max;
        }
        return result;

    }
}

solution2 双端队列

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums.length == 0 || k == 0) return nums; //判空

        int[] result = new int[nums.length-k+1]; //返回的结果

        Deque<Integer> dq = new ArrayDeque<>(); // 双端队列，从小到大
        for (int i = 0; i < nums.length ;i ++){
            if (!dq.isEmpty() && dq.peek() < i - k + 1) {
				dq.poll();
			}
            //移除队列内比要插入的小的元素，保证最后一位为最大值
            while (!dq.isEmpty() && nums[dq.peekLast()] <= nums[i]) {
                dq.pollLast();
            }
            dq.offer(i);
            if (i-k+1 >= 0){ //遍历到第3个开始存值
                result[i-k+1] = nums[dq.peek()];
            }
        }
        return result;

    }
}

solution3 分块法

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (nums == null || nums.length == 0) {
            return null;
        }
        int[] maxfromleft = new int[nums.length];
        int[] maxfromright = new int[nums.length];

        maxfromleft[0] = nums[0];
        maxfromright[nums.length - 1] = nums[nums.length - 1];
        //分块 整两个数组记录
        for (int i = 1;i < nums.length;i++) {
            //从左到右遍历  保证块内从左到右增大
            if (i%k == 0) maxfromleft[i] = nums[i];
            else maxfromleft[i] = Math.max(maxfromleft[i-1],nums[i]);

            //从右到左遍历 保证块内从右到左递增
            int j = nums.length - 1 - i;
            if (j%k == 0) maxfromright[j] = nums[j];
            else maxfromright[j] = Math.max(maxfromright[j+1],nums[j]);
        }
        int[] output = new int[nums.length - k + 1];
        for (int i = 0;i < nums.length - k +1;i ++) {
            output[i] = Math.max(maxfromleft[i+k-1],maxfromright[i]);
            //取窗口涉及到的左块内最右的值，右块内最左的值进行比较
        }
        return output;
    }
}

//用lamda
 public static int[] slidingWindowMax(final int[] in, final int w) {
    final int[] max_left = new int[in.length];
    final int[] max_right = new int[in.length];

    max_left[0] = in[0];
    max_right[in.length - 1] = in[in.length - 1];

    for (int i = 1; i < in.length; i++) {
        max_left[i] = (i % w == 0) ? in[i] : Math.max(max_left[i - 1], in[i]);

        final int j = in.length - i - 1;
        max_right[j] = (j % w == 0) ? in[j] : Math.max(max_right[j + 1], in[j]);
    }

    final int[] sliding_max = new int[in.length - w + 1];
    for (int i = 0, j = 0; i + w <= in.length; i++) {
        sliding_max[j++] = Math.max(max_right[i], max_left[i + w - 1]);
    }