【转载】 深度学习——Xavier初始化方法

版权声明：本文为CSDN博主「shuzfan」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/shuzfan/article/details/51338178

=================================

“Xavier”初始化方法是一种很有效的神经网络初始化方法，方法来源于2010年的一篇论文《Understanding the difficulty of training deep feedforward neural networks》，可惜直到近两年，这个方法才逐渐得到更多人的应用和认可。
为了使得网络中信息更好的流动，每一层输出的方差应该尽量相等。
基于这个目标，现在我们就去推导一下：每一层的权重应该满足哪种条件。

文章先假设的是线性激活函数，而且满足0点处导数为1，即

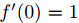
现在我们先来分析一层卷积：

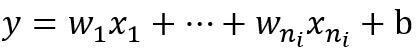
其中ni表示输入个数。

根据概率统计知识我们有下面的方差公式：

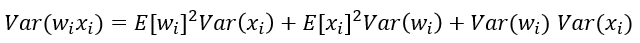
特别的，当我们假设输入和权重都是0均值时（目前有了BN之后，这一点也较容易满足），上式可以简化为：

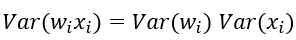
进一步假设输入x和权重w独立同分布，则有：

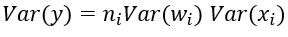
于是，为了保证输入与输出方差一致，则应该有：

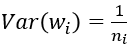
对于一个多层的网络，某一层的方差可以用累积的形式表达：

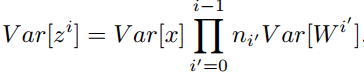
特别的，反向传播计算梯度时同样具有类似的形式：

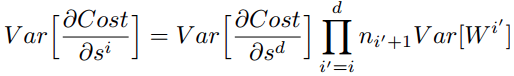
综上，为了保证前向传播和反向传播时每一层的方差一致，应满足：

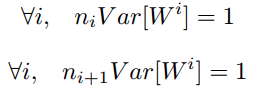
但是，实际当中输入与输出的个数往往不相等，于是为了均衡考量，最终我们的权重方差应满足：

———————————————————————————————————————

———————————————————————————————————————

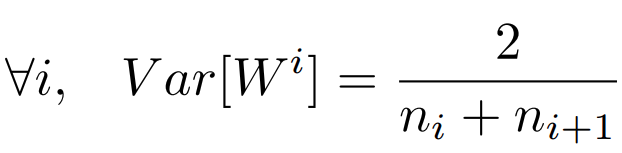
学过概率统计的都知道 [a,b] 间的均匀分布的方差为：

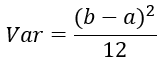
因此，Xavier初始化的实现就是下面的均匀分布：

——————————————————————————————————————————

——————————————————————————————————————————

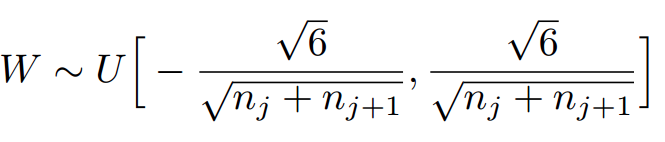
下面，我们来看一下caffe中具体是怎样实现的，代码位于include/caffe/filler.hpp文件中。

template <typename Dtype>
class XavierFiller : public Filler<Dtype> {
 public:
  explicit XavierFiller(const FillerParameter& param)
      : Filler<Dtype>(param) {}
  virtual void Fill(Blob<Dtype>* blob) {
    CHECK(blob->count());
    int fan_in = blob->count() / blob->num();
    int fan_out = blob->count() / blob->channels();
    Dtype n = fan_in;  // default to fan_in
    if (this->filler_param_.variance_norm() ==
        FillerParameter_VarianceNorm_AVERAGE) {
      n = (fan_in + fan_out) / Dtype(2);
    } else if (this->filler_param_.variance_norm() ==
        FillerParameter_VarianceNorm_FAN_OUT) {
      n = fan_out;
    }
    Dtype scale = sqrt(Dtype(3) / n);
    caffe_rng_uniform<Dtype>(blob->count(), -scale, scale,
        blob->mutable_cpu_data());
    CHECK_EQ(this->filler_param_.sparse(), -1)
         << "Sparsity not supported by this Filler.";
  }
};

由上面可以看出，caffe的Xavier实现有三种选择

（1） 默认情况，方差只考虑输入个数：

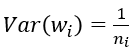
（2） FillerParameter_VarianceNorm_FAN_OUT，方差只考虑输出个数：

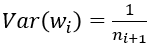
（3） FillerParameter_VarianceNorm_AVERAGE，方差同时考虑输入和输出个数：

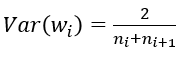
之所以默认只考虑输入，我个人觉得是因为前向信息的传播更重要一些

————————————————