[USACO22FEB] Paint by Rectangles P 题解
前言
没用线段树的小常数、小短码。
题目链接:洛谷。
题意简述
给出 \(n\) 个平行于坐标轴的矩形,各边所在直线互不重合,钦定最外面为白色,对这个平面图黑白染色,分别求黑色块数和白色块数。
题目分析
这道题扫描线一眼题吧?所以考虑从左到右扫描线。初始白色有 \(1\) 块。
加边
先考虑加边。加入一条竖边 \([l, r]\),就把这段区间异或一下,统计新增的白色块数和黑色块数。我们需要知道这条边对应的区间有多少个块。由于这些连通块是黑白相间的,我们只需要确定下面开始第一块的颜色是什么就行了。
记有 \(cnt\) 个块,黑色为 \(1\),白色为 \(0\),记最下面一块颜色是 \(c \in \lbrace 0, 1 \rbrace\)。
那么就让 \(c\) 的块数加上 \(\left \lceil \cfrac{cnt}{2} \right \rceil\);让 \(c \operatorname{xor} 1\) 的块数加上 \(\left \lfloor \cfrac{cnt}{2} \right \rfloor\)。
那么如何知道块数和最下面的颜色呢?使用树状数组维护即可。
我们维护横边。加边的时候用树状数组将 \(l, r\) 分别单点加一。那么块数就是 \([l + 1, r - 1]\) 中横边个数加一;最下方的颜色就查询 \(l\) 以下有多少条横边,若是奇数个,则是白色,反之是黑色。
这么说也许不清晰,来看看样例:
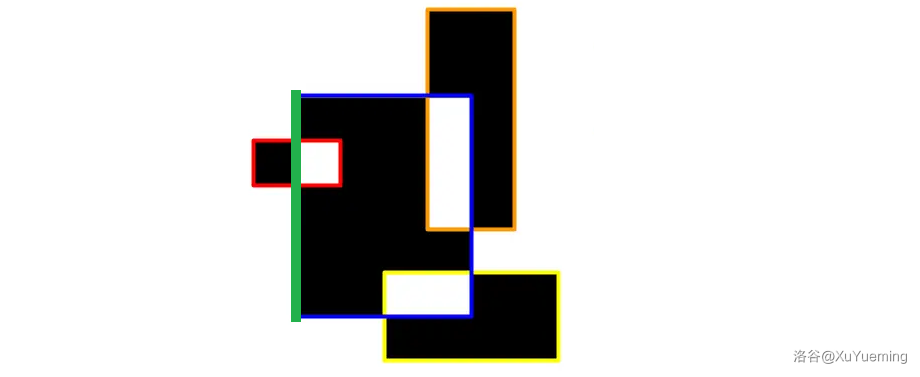
加入这条绿色的竖边。块数 \(cnt = 3\),由于 \(l\) 下方横边数量 \(0\) 是偶数,所以最下方颜色是黑色。就上黑色块数加上 \(\left \lceil \cfrac{3}{2} \right \rceil = 2\),白色块数加上 \(\left \lfloor \cfrac{3}{2} \right \rfloor = 1\)。
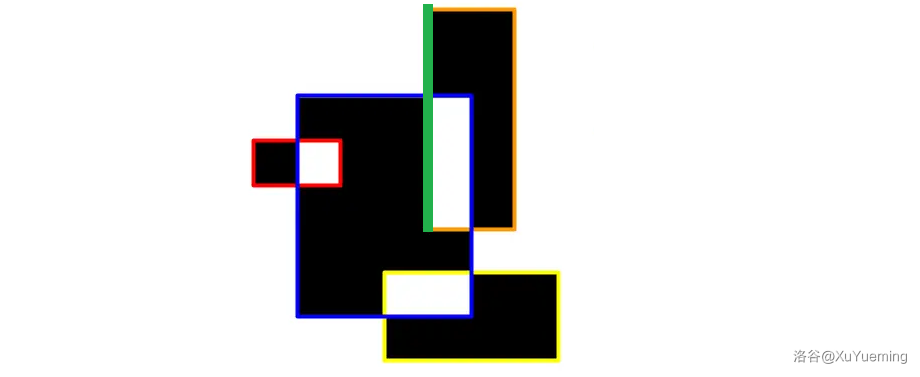
再来看看这条绿边。块数 \(cnt = 2\),由于 \(l\) 下方横边数量 \(3\) 是奇数,所以最下方颜色是白色。就上黑色块数加上 \(\left \lceil \cfrac{2}{2} \right \rceil = 1\),白色块数加上 \(\left \lfloor \cfrac{2}{2} \right \rfloor = 1\)。
删边
删边也同理,但是略有不同。记删边后,这里有 \(cnt\) 个块,最下面一块颜色是 \(c \in \lbrace 0, 1 \rbrace\)。
注意,如果此时 \(cnt = 1\),则表示这是一条结束的边。之前我们将 \(c\) 统计成多个块,但这时候它们到一起去了,所以要将 \(c\) 的块数减一。
其他情况注意最下面的颜色是和加边相反的,以及最上面的块和最下面的块是和外面的连成一个块,不做统计。
看看样例:
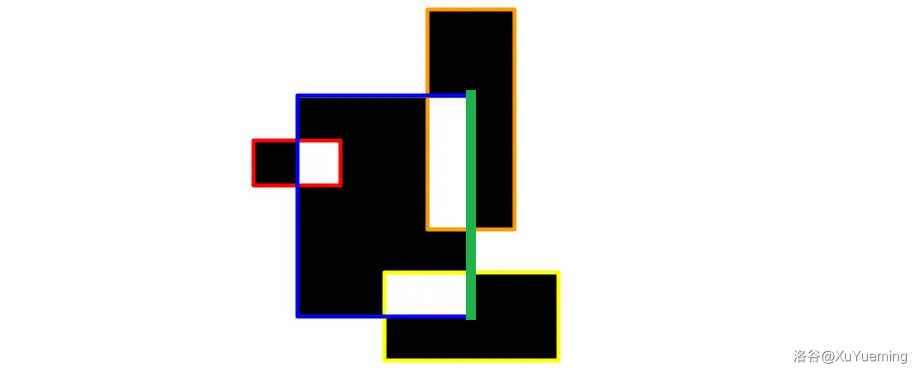
删去这条绿色的边。\(l\) 下面横边数量 \(1\) 是奇数,所以最下方颜色是黑色(而不是白色)。块数 \(cnt = 3\),但是最上面的黑色块属于橙色矩形,最下面的黑色块属于黄色矩形,这些块之前已经统计过了。所以让黑色块数加上 \(\left \lfloor \cfrac{cnt - 2}{2} \right \rfloor = 0\),白色块数加上 \(\left \lceil \cfrac{cnt - 2}{2} \right \rceil = 1\)。
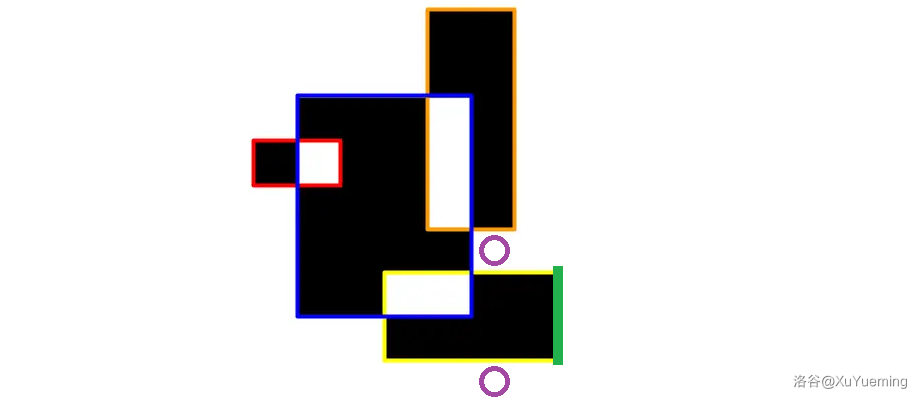
删去这条绿色的边。\(l\) 下面横边数量 \(0\) 是偶数,所以最下方颜色是白色。块数 \(cnt = 1\),这就是上文提到的情况:在两个紫色圆圈处,我们将它统计成两个白色部分,而实际上它是一个块,所以将白色块数减一。
处理
这样就结束了吗?不不不,你可以看看下面的最简单的反例。

没错,只有一个矩形。我们会发现在删去右边的竖边时,不应该将白色块数减一。
如果这样的矩形不止一个,那么白色的块数就被少减了很多。
我们将白色块数加上矩形互相相交的连通块个数就行了,吗?但是还是不对,不光光只是外面的白色平面,我们考虑矩形完全包含的情况。

我们发现,处理里面红色矩形的时候,也会将黑色块数多减了一。此时,相当于红色矩形处在一个背景色是黑色的平面内,似乎是一个更小的子问题。
所以,我们在开始处理一个矩形互相相交的连通块时,首先看看它是处在一个黑色还是白色的平面内,将这个颜色数量加一,然后再处理这个子问题,这样就不会出现问题。
代码
时间复杂度 \(n (\log n + \alpha(n))\)。
具体注释看代码吧,略去了快读快写,目前是 Rank1。
// #pragma GCC optimize(3)
// #pragma GCC optimize("Ofast", "inline", "-ffast-math")
// #pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <iostream>
#include <cstdio>
#define debug(a) cerr << "Line: " << __LINE__ << " " << #a << endl
#define print(a) cerr << #a << "=" << (a) << endl
#define file(a) freopen(#a".in", "r", stdin), freopen(#a".out", "w", stdout)
#define main Main(); signed main(){ return ios::sync_with_stdio(0), cin.tie(0), Main(); } signed Main
using namespace std;
#include <set>
int n, T;
int L[100010 << 1], R[100010 << 1];
// L[i] ~ R[i] 是横坐标为 i 的竖边
int toleft[100010 << 1], bl[100010 << 1], p[100010 << 1];
// toleft[i] 是将一个矩形右边的竖边映射到左边的竖边
// bl[i] 是一个左边的竖边所在矩形的编号
// p[i] 是一条横边所对应的左边的竖边编号
set<int> S;
// 用 set 维护目前出现的所有横边
struct Bit_Tree{
constexpr inline int lowbit(const int x){ return x & -x; }
int tree[100010 << 1];
void modify(int p, int v){ for (int i = p; i <= n; i += lowbit(i)) tree[i] += v; }
int query(int p){ int res = 0; for (int i = p; i; i -= lowbit(i)) res += tree[i]; return res; }
int query(int l, int r){ return r < l ? 0 : query(r) - query(l - 1); }
} yzh;
// yzh 是树状数组
int fa[100010];
bool vis[100010];
int get(int x){ return fa[x] == x ? x : fa[x] = get(fa[x]); }
void merge(int a, int b){ fa[get(a)] = get(b); }
// 并查集维护矩形连通性
signed main(){
read(n, T);
for (int i = 1, x1, y1, x2, y2; i <= n; ++i){
read(x1, y1, x2, y2);
L[x1] = L[x2] = y1, R[x1] = R[x2] = y2;
toleft[x2] = p[y1] = p[y2] = x1, bl[x1] = i, fa[i] = i;
}
n <<= 1;
for (int i = 1; i <= n; ++i){
if (!toleft[i]) S.insert(L[i]), S.insert(R[i]);
for (set<int>::iterator it = S.upper_bound(L[i]); it != S.end() && *it < R[i]; it = S.erase(it))
merge(bl[p[L[i]]], bl[p[*it]]);
if (toleft[i]) S.erase(L[i]), S.erase(R[i]);
// 发现只用在加入和删除竖边时,和已经存在的横边的矩形都有相交,并查集合并即可
}
long long ans[2] = {1, 0};
for (int i = 1; i <= n; ++i){
if (!toleft[i] && !vis[get(bl[i])]) vis[get(bl[i])] = true, ++ans[yzh.query(L[i]) & 1];
// 表明是这个连通块第一次出现,将背景色块数加一
if (!toleft[i]){ // 加边
int cnt = yzh.query(L[i] + 1, R[i] - 1) + 1; // 块数
if (yzh.query(L[i]) & 1){ // 最下面颜色是白色
ans[0] += (cnt + 1) >> 1, ans[1] += cnt >> 1;
} else {
ans[1] += (cnt + 1) >> 1, ans[0] += cnt >> 1;
}
yzh.modify(L[i], 1), yzh.modify(R[i], 1);
} else { // 删边
int cnt = yzh.query(L[i] + 1, R[i] - 1) + 1;
if (cnt == 1) --ans[(yzh.query(L[i]) & 1) ^ 1];
else if (yzh.query(L[i]) & 1){
ans[1] += (cnt - 2 + 1) >> 1, ans[0] += (cnt - 2) >> 1;
} else {
ans[0] += (cnt - 2 + 1) >> 1, ans[1] += (cnt - 2) >> 1;
}
yzh.modify(L[i], -1), yzh.modify(R[i], -1);
}
}
if (T == 1) write(ans[0] + ans[1]);
else write(ans[0], ' ', ans[1]);
return 0;
}
后记
比用欧拉公式,线段树加并查集的做法是不是好多了?
[USACO22FEB] Paint by Rectangles P 题解的更多相关文章
- ZOJ - 3781 Paint the Grid Reloaded 题解
题目大意: 给一个n*m的X O构成的格子,对一个点操作可以使与它相连通的所有一样颜色的格子翻转颜色(X—>O或O—>X),问给定的矩阵最少操作多少次可以全部变成一样的颜色. 思路: 1. ...
- AtCoder瞎做第二弹
ARC 067 F - Yakiniku Restaurants 题意 \(n\) 家饭店,\(m\) 张餐票,第 \(i\) 家和第 \(i+1\) 家饭店之间的距离是 \(A_i\) ,在第 \( ...
- [BZOJ 1260][CQOI2007]涂色paint 题解(区间DP)
[BZOJ 1260][CQOI2007]涂色paint Description 假设你有一条长度为5的木版,初始时没有涂过任何颜色.你希望把它的5个单位长度分别涂上红.绿.蓝.绿.红色,用一个长度为 ...
- 【题解】 bzoj1260: [CQOI2007]涂色paint (区间dp)
bzoj1260,懒得复制,戳我戳我 Solution: 这种题目我不会做qwq,太菜了 区间打牌(dp) 用f[l][r]表示从l到r最少需要染几次色. 状态转移方程: 1.\(f[l][r]=mi ...
- ZOJ 2747 Paint the Wall(离散化+暴力)题解
题意:给你一个面,然后涂颜色,问你最后剩多少颜色,每种颜色面积. 思路:第一反应是二维线段树,代码又臭又长,可以做.但是这题暴力+离散化就可以过.可以看到他给的n只有100,也就是说最坏情况下会涂10 ...
- HDU1510 White rectangles( 乱搞 O(n^3) )题解
思路: 友谊赛的时候一直想到了,但是没想出来怎么遍历才能找到所有矩阵,卡住了. 这里讲一下完整思路:我们用一个num[i][j]表示第i行第j列每一列连续的白色格子数量,然后我们定义一个MIN,并且每 ...
- [CQOI2007]涂色paint(BZOJ 1260)题解
题目描述 假设你有一条长度为5的木版,初始时没有涂过任何颜色.你希望把它的5个单位长度分别涂上红.绿.蓝.绿.红色,用一个长度为5的字符串表示这个目标:RGBGR. 每次你可以把一段连续的木版涂成一个 ...
- 题解 P3117 【[USACO15JAN]牛的矩形Cow Rectangles】
暴力什么的就算了,贪心他不香吗 这题其实如果分开想,就三种情况需要讨论:(由于不会发图,只能手打) 1) 5 . . . . . 4 . . . . . 3 . . . H . 2 . . G . . ...
- LeetCode All in One题解汇总(持续更新中...)
突然很想刷刷题,LeetCode是一个不错的选择,忽略了输入输出,更好的突出了算法,省去了不少时间. dalao们发现了任何错误,或是代码无法通过,或是有更好的解法,或是有任何疑问和建议的话,可以在对 ...
- noip2016十连测题解
以下代码为了阅读方便,省去以下头文件: #include <iostream> #include <stdio.h> #include <math.h> #incl ...
随机推荐
- 一文了解Spark引擎的优势及应用场景
Spark引擎诞生的背景 Spark的发展历程可以追溯到2009年,由加州大学伯克利分校的AMPLab研究团队发起.成为Apache软件基金会的孵化项目后,于2012年发布了第一个稳定版本. 以下是S ...
- app备案
最近app要求备案,使用阿里云备案 安卓可以上传apk获取信息,那么ios怎么弄呢 https://zhuanlan.zhihu.com/p/660738854?utm_id=0 查看的时候需要使用m ...
- navicat 连接oracle 失败
问题: 1.使用Navicat连接Oracle数据库时,报错ORA-12504: TNS:listener was not given the SERVICE_NAME in CONNECT_DATA ...
- python 动态导入模块并结合反射,动态获取类、方法(反射太好用),动态执行方法
背景: 关键字驱动框架,不同的关键字方法分别定义在不同的类,真正执行关键字方法又在不同的类(简称A),这样就需要在执行前,要在文件A下import要使用的模块,如果有很多页面操作或很多模块时,就需要每 ...
- iOS登陆界面切换到注册界面并返回的UI设计(简易向)
功能实现 从登陆界面进入注册界面 从注册界面返回登陆界面 功能实现思路 在网上搜了搜发现各位大神用的是navigation,但个人感觉没(zhen)大(ting)必(bu)要(dong).所以在这里提 ...
- 使用Redis+SpringBoot实现定时任务测试
Redis实现定时任务是基于对RedisKey值的监控 具体代码实现: 代码GitHub地址:https://github.com/Tom-shushu/Project 建一个SpringBoot项目 ...
- HTTP协议 学习:1-报文分析
HTTP协议 学习:1-报文分析 背景 上一讲我们介绍了HTTP协议的一些 概念 ,对HTTP协议有了一个基础的认识. 正如之前学习MQTT协议一样,我们需要对HTTP的报文进行分析. HTTP 报文 ...
- 机器学习(三)——K最临近方法构建分类模型(matlab)
K最临近(K-Nearest Neighbors,KNN)方法是一种简单且直观的分类和回归算法,主要用于分类任务.其基本原理是用到表决的方法,找到距离其最近的K个样本,然后通过K个样本的标签进行表决, ...
- 《DNK210使用指南 -CanMV版 V1.0》第五章 编译CanMV固件
第五章 编译CanMV固件 1)实验平台:正点原子DNK210开发板 2) 章节摘自[正点原子]DNK210使用指南 - CanMV版 V1.0 3)购买链接:https://detail.tmall ...
- 工控必备!NXP i.MX 8M Mini开发板规格书资料分享,高性能低功耗!
1 核心板简介 创龙科技SOM-TLIMX8-B是一款基于NXP i.MX 8M Mini的四核ARM Cortex-A53 + 单核ARM Cortex-M4异构多核处理器设计的高端工业级核心板,A ...
