[P2416 泡芙] 题解报告

题目链接：P2416 泡芙

简化题意

给定一个无向图 \(G\)，每条边有边权 \(0 / 1\)，现给定 \(m\) 组询问，每次询问形如 \(s, t\)，问是否可以从 \(s\) 走到 \(t\)，边权和为正数且不会重复经过一条边。

题目分析

本题可以使用 tarjan 算法。

可以想一下，如果在从 \(s\) 到 \(t\) 的路径上有一个环，那么我们一定会选择经过这个环。因为走完整条环之后可以回到起点，不会重复经过某一条路，而且还有可能多加一点边权。

因此考虑缩点。使用 tarjan 算法将所有边双连通分量缩成点。

边权转点权时，设有边 \((u, v)\)，边权为 \(1\) ，那么可以新建一个节点，将边权存在这个点的点权上。

如下图：

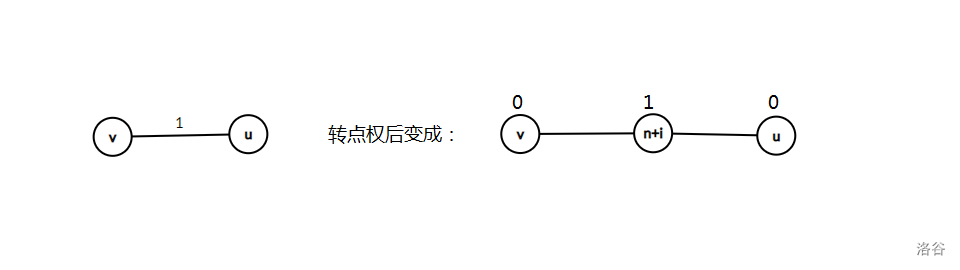
缩点时将每个新点的点权设成连通分量内所有点的点权的或，换言之，就是设置成“连通分量内是否有点权为 \(1\) 的点 （若有则为 \(1\)，否则为 \(0\)）”。

缩点之后图会变成一棵树。之后 \(m\) 次操作就是询问从 \(u\) 到 \(v\) 两个点之间的路径权值和是否大于等于 \(1\)，可以使用树上差分解决。

时间复杂度大概是 \(O(m + Q \log n)\) 的样子。跑的大概没有题解里的其他 dalao 快

CODE

// Author:Lcy
// Date:2022.07.15

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 300010;

int n, m;
int h[N << 1], e[N << 2], ne[N << 2], w[N << 1], idx = 1;
int stk[N << 1], timestamp, top;
int dfn[N << 1], low[N << 1], val[N << 1];
int color[N << 1];
int cnt, fa[N << 1], dep[N << 1], sz[N << 1];
int son[N << 1], s[N << 1], Top[N << 1], id[N << 1];
int from[N], to[N];

void add(int a, int b)
{
	e[ ++ idx] = b, ne[idx] = h[a], h[a] = idx;
}

void tarjan(int u, int from)
{
	dfn[u] = low[u] = ++ timestamp;
	stk[ ++ top] = u;

	for (int i = h[u]; i; i = ne[i])
	{
		int j = e[i];
		if (!dfn[j]) {
			tarjan(j, i);
			low[u] = min(low[u], low[j]);
		}
		else if (i != (from ^ 1))
			low[u] = min(low[u], dfn[j]);
	}

	if (dfn[u] == low[u])
	{
		cnt ++ ;
		int y;
		do {
			y = stk[top -- ];
			val[cnt] |= w[y];
			color[y] = cnt;
		} while (y != u);
	}
}

void dfs1(int u, int father, int depth)
{
	fa[u] = father, dep[u] = depth, sz[u] = 1;
	s[u] = s[fa[u]] + (val[u] == 1);

	for (int i = h[u]; i; i = ne[i])
	{
		int j = e[i];
		if (j == father) continue;
		dfs1(j, u, depth + 1);
		sz[u] += sz[j];
		if (sz[son[u]] < sz[j]) son[u] = j;
	}
}

void dfs2(int u, int t)
{
	Top[u] = t, id[u] = ++ cnt;

	if (!son[u]) return;
	dfs2(son[u], t);

	for (int i = h[u]; i; i = ne[i])
	{
		int j = e[i];
		if (j == fa[u] || j == son[u]) continue;
		dfs2(j, j);
	}
}

int lca(int u, int v)
{
	while (Top[u] != Top[v])
	{
		if (dep[Top[u]] <= dep[Top[v]]) swap(u, v);
		u = fa[Top[u]];
	}
	if (dep[u] > dep[v]) swap(u, v);
	return u;
}

bool query(int u, int v)
{
	int LCA = lca(u, v);
	return (s[u] - s[LCA] + s[v] - s[LCA] + val[LCA]);
}

int main()
{
	scanf("%d%d", &n, &m);

	for (int i = 1; i <= m; i ++ )
	{
		int z;
		scanf("%d%d%d", &from[i], &to[i], &z);
		add(from[i], n + i), add(n + i, from[i]);
		add(n + i, to[i]), add(to[i], n + i);
		w[n + i] = z;
	}

	tarjan(1, -1);

	memset(h, 0, sizeof h);
	memset(e, 0, sizeof e);
	memset(ne, 0, sizeof ne);
	idx = 0;

	for (int i = 1; i <= m; i ++ ) {
		if (color[from[i]] != color[n + i])
			add(color[from[i]], color[n + i]),
			add(color[n + i], color[from[i]]);
		if (color[to[i]] != color[n + i])
			add(color[to[i]], color[n + i]),
			add(color[n + i], color[to[i]]);
	}

	dfs1(1, -1, 1), dfs2(1, 1);

	int Q;
	scanf("%d", &Q);

	while (Q -- )
	{
		int u, v;
		scanf("%d%d", &u, &v);
		(query(color[u], color[v])) ? (puts("YES")) : (puts("NO"));
	}

	return 0;
}