Okio 1.9简单入门

Okio 1.9简单入门

Okio库是由square公司开发的，补充了java.io和java.nio的不足，更加方便，快速的访问、存储和处理你的数据。而OkHttp的底层也使用该库作为支持。

该库极大的简化I/O操作。

Gradle引用如下(最新版：1.9 )
compile 'com.squareup.okio:okio:1.9.0'

Okio类作为OkIo库暴露给外部使用的类，提供大量的静态方法；

其有两个关键的接口，Sink和Source，继承了Closeable接口；

Sink可以简单的看做OutputStream；->写操作!   ->通过一个Sink获得一个BufferedSink。
Source可以简单的看做InputStream。->读操作! ->通过一个Source获得BufferedSource，

如下图：

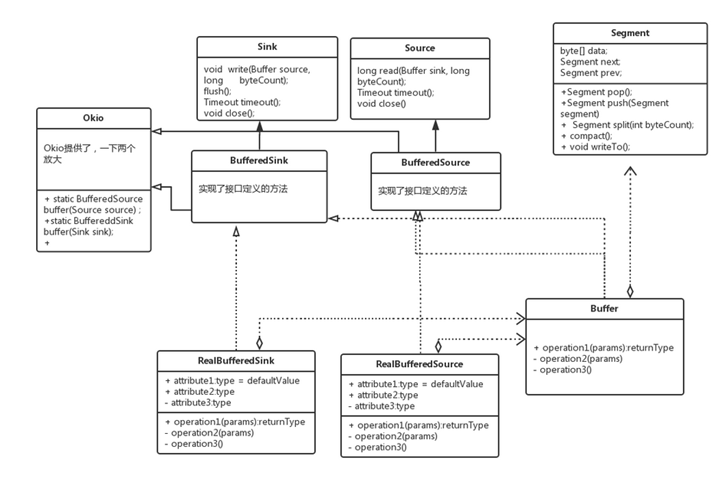
Sink 与Source类的结构图如下：

说明：

Sink 有个子类接口 BufferddSink ：定义了一系列写入缓存区的方法 
实现类 RealBufferedSink

Source 有个子类接口 BufferedSource ：定义了一系列读取缓存区的方法

实现类RealBufferedSource

支持gzip压缩的实现类GzipSink和GzipSource及压缩类DeflaterSink和InflaterSource；

实现类 RealBufferedSink 、RealBufferedSource结构：

Buffer类
Buffer类操作写动作，但是数据并没真正的完成写，而是保存在链表（Segment双向链表）中；

具体使用

对Okio库的整体框架有了基本了解，那么就该实际操作了。

具体步骤如下：

1.调用Okio类的静态方法获取Source(Sink)

2.调用Okio类库的静态方法，通过刚才获取的Source(Sink)获取BufferedSource（BufferedSink）

3.对缓冲区根据实际需求做相应操作

4.若是Sink，须将调用flush()

5.最后close掉，避免内存泄漏

读取文件

一．在项目根目录下新建文件“test.txt”,并写入一些文字;

二．新建Class:-> Okio_Demo

三．进入读写操作；

四．在类中新建 main()方法，进行测试！
说明：所有功能都是在类中写main()方法中进行测试!!

如下图：

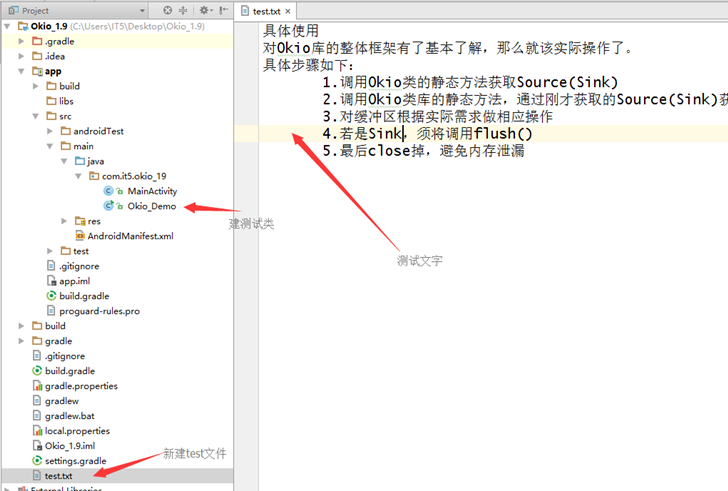
创建文件并写数据

);
        } catch (IOException e) {
            e.printStackTrace();
        }
    }

Buffer 读操作：

/**
 * 读buffer
 */
public static void sourceFromInputStream(){
    //1.构建字节数组流
        try {
            InputStream
                in = new ByteArrayInputStream(("adasfdsaf").getBytes());
            //2.缓冲源
            Source source=Okio.source(in);
            //3.buffer
            Buffer sink = new Buffer();
            source.read(sink,in.read());
            //4.将数据读入buffer
            System.out.print(sink.readUtf8());
        } catch (Exception e) {
            e.printStackTrace();
        }
}

Okio工具类—ByteString类，这个类可以用来做各种变化，它将byte转会为String，而这个String可以是utf8的值，也可以是base64后的值，也可以是md5的值，也可以是sha256的值，总之就是各种变化，最后取得你想要的值。

如：

ByteString.of("ss".getBytes()).base64();
ByteString.of("ss".getBytes()).md5();
ByteString.of("ss".getBytes()).sha1();
ByteString.of("ss".getBytes()).sha256();

最后借用一个大牛的类图!

Okio的类图关系如下:

Demo下载

官网地址：

1.OkioAPI

2.Okio GitHub地址

来自为知笔记(Wiz)