EOJ 1127. 多边形面积（计算几何）

题目链接：1127. 多边形面积（计算几何）

题意

按逆时针顺序给出 \(n\) 个点的坐标，求这些点围成的多边形的面积。

思路

选择多边形上的一个点，然后每次枚举之后的两个点，计算叉积，注意要保留符号，对所有的叉积的结果相加就是多边形的面积。

举个栗子：

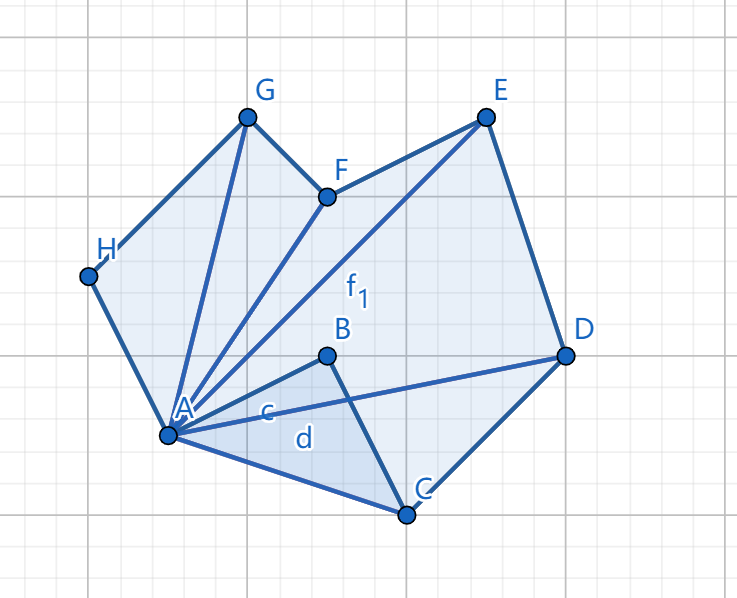
计算上图多边形 \(ABCDEFGH\) 的面积，选择 \(A\) 点，则面积等于 \(\frac{1}{2} (\boldsymbol {AB \times AC} + \boldsymbol {AC \times AD} + \boldsymbol {AD \times AE} + \boldsymbol {AE \times AF} + \boldsymbol {AF \times AG} + \boldsymbol {AG \times AH})\)。其中 \(\triangle ABC\) 的面积是负的，而 \(\triangle ACD\) 与 \(\triangle ADE\) 的面积都是正的，则多边形 \(ABCDE\) 的面积相当于多边形 \(ACDE\) 的面积减去 \(\triangle ABC\) 的面积。

代码

#include <cstdio>
#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef double db;
const db eps = 1e-10;
const db pi = acos(-1.0);
const ll inf = 0x3f3f3f3f3f3f3f3f;
const ll maxn = 100 + 10;

inline int dcmp(db x) {
    if(fabs(x) < eps) return 0;
    return x > 0? 1: -1;
}

class Point {
public:
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) {}
    void input() {
        scanf("%lf%lf", &x, &y);
    }
    bool operator<(const Point &a) const {
        return (!dcmp(x - a.x))? dcmp(y - a.y) < 0: x < a.x;
    }
    bool operator==(const Point &a) const {
        return dcmp(x - a.x) == 0 && dcmp(y - a.y) == 0;
    }
    db dis2(const Point a) {
        return pow(x - a.x, 2) + pow(y - a.y, 2);
    }
    db dis(const Point a) {
        return sqrt(dis2(a));
    }
    db dis2() {
        return x * x + y * y;
    }
    db dis() {
        return sqrt(dis2());
    }
    Point operator+(const Point a) {
        return Point(x + a.x, y + a.y);
    }
    Point operator-(const Point a) {
        return Point(x - a.x, y - a.y);
    }
    Point operator*(double p) {
        return Point(x * p, y * p);
    }
    Point operator/(double p) {
        return Point(x / p, y / p);
    }
    db dot(const Point a) {
        return x * a.x + y * a.y;
    }
    db cross(const Point a) {
        return x * a.y - y * a.x;
    }
};

Point p[maxn];

int n;

db area() {
    if(n < 3) return 0.0;
    db ans = 0.0;
    for(int i = 2; i < n; ++i) {
        ans += (p[i] - p[1]).cross(p[i + 1] - p[1]);
    }
    return ans * 0.5;
}

int main() {
    while(~scanf("%d", &n) && n) {
        db s = 0;
        for(int i = 1; i <= n; ++i) {
            p[i].input();
        }
        s = area();
        printf("%.1lf\n", fabs(s));
    }
    return 0;
}