[CERC2016]:凸轮廓线Convex Contour（模拟+数学）

题目描述

一些几何图形整齐地在一个网格图上从左往右排成一列。它们占据了连续的一段横行，每个位置恰好一个几何图形。每个图形是以下的三种之一：
$1.$一个恰好充满单个格子的正方形。
$2.$一个内切于单个格子的圆。
$3.$一个底边与格子重合的等边三角形。

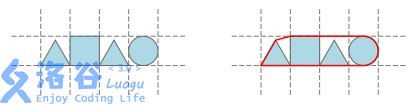
已知每个格子的边长都为$1$，请求出这些几何图形的凸包的周长。

---

输入格式

第一行包含一个正整数$n$，表示几何图形的个数。
第二行包含$n$个字符，从左往右依次表示每个图形，$"S"$表示正方形，$"C"$表示圆形，$"T"$表示等边三角形。

---

输出格式

输出一行一个实数，即凸包的周长。与答案的绝对或相对误差不超过$10^{-6}$时被认为是正确的。

---

样例

样例输入：

4
TSTC

样例输出：

9.088434417

---

数据范围与提示

$1\leqslant n\leqslant 20$

---

题解

突然看到自己刚学$OI$时的题解，已经是一年前的题解了（有同学说，一年前的我都能掉打现在的他），那是满是美好的回忆，没有现在临近$CSP-S$痛苦的日常。

附上一年前的题解链接：题解 P3680 【[CERC2016]凸轮廓线 Convex Contour】。

上面这篇题解中有错误（还是当时菜），评论区已经有人指正了，在此不再赘述。

这天又打了一遍，在原来的基础上讲一讲自己现在对这道题的心得和体会。

不知道为什么数据范围是$20$，总之我的时间复杂度是$\Theta(n)$的……

显然中间无论是什么形状都是无所谓的，因为无论是什么图形

先来考虑正方形和圆形在两端的情况，这样会简单很多，因为它们的高度都是$1$，这样我们无非就是需要考虑两头是什么形状就好了：

　　$\alpha.$如果两头都是正方形，那么答案就是$2\times n+2\downarrow$

　　

　　$\beta.$如果是一个正方形，一个圆形，答案就是$2\times n+\dfrac{\frac{\sqrt{3}}{2}\pi}{2}$

　　

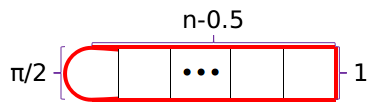
　　$\gamma.$如果两头都是圆形，那么答案就是$2\times n-2+\pi\downarrow$

　　

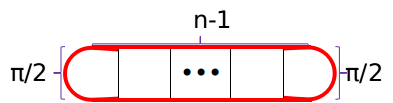
再来考虑三角形在两端的情况，远没有你想象的简单。

你以为是这样的：

然而是事实这样的：

于是你就弃掉了它……

如果你还能看到这里，就说明你还有希望，那么我们先来考虑三角形在一头，下一个是正方形的情况：

你以为是这样：

然而事实又是这样：

难点在于处理“悬空”的那条线的长度，但是我们发现了如下的一个直角三角形：

可以先求出来这个直角三角形的两个直角边的长度再通过勾股定理求出斜边长，不妨对这个直角三角形作出如下定义：

因为边长为$1$的等边三角形的高为$\frac{sqrt{3}}{2}$，所以我们可以知道$a=1-\frac{sqrt{3}}{2}$，$b$很好求，就是开头三角形的个数$-0.5$。

三角形在最后同理，在此不再赘述。

于是我们解决了三角形$+$正方形的情况。

考虑最后的也是最难的三角形$+$圆形的情况：

你以为是这样的：

然而事实又是这样：

上图中粗的红线是圆的切线，那么我们又可以找到一个三角形：

不妨再做出如下定义：

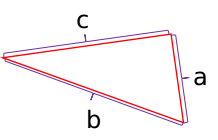
$a$就是圆形边长，很好求，难点变成了求$b$。

再回到上一张图，又发现了一个三角形：

再放大这个三角形：

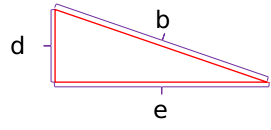
$d$就是$\sqrt{3}-1$，$e$则是开头三角形的个数，于是我们可以得到$b$。

所有情况枚举完了，这道题也就轻松解决了。

时间复杂度：$\Theta(n)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
char ch[20];
double ans,p;
int n,flag;
int main()
{
	scanf("%d%s",&n,ch+1);
	ans+=n-1;
	if(ch[1]=='C')flag=2,ans+=M_PI/2;
	if(ch[n]=='C')ans+=M_PI/2;
	if(ch[1]=='T')p+=1.0,flag=0,ans+=1.5;
	if(ch[n]=='T')ans+=1.5;
	if(ch[1]=='S')flag=1,ans+=2.5;
	if(ch[n]=='S')ans+=1.5;
	for(int i=2;i<=n;i++)
		switch(ch[i])
		{
			case 'T':p+=1.0;break;
			case 'S':
				switch(flag)
				{
					case 0:
						ans+=sqrt((p-0.5)*(p-0.5)+(7.0/4.0-sqrt(3)))+1.0;
						p=0;
						flag=1;
					break;
					case 1:
						ans+=p+1.0;
						p=0;
					break;
					case 2:
						ans+=p+1.5;
						p=0;
						flag=1;
					break;
				}
			break;
			case 'C':
				switch(flag)
				{
					case 0:
					{
						double x=1.0*(p);
						double y=(sqrt(3)/2.0-0.5);
						double z=sqrt(x*x+1.0-sqrt(3)/2.0);
						double len1=sqrt(x*x+1.0-sqrt(3)/2.0-0.25);
						double o=M_PI/2.0-atan(y/x)-acos(0.5/z);
						double len2=0.5*o;
						p=0;
						ans+=len1+len2;
						flag=2;
					}
					break;
					case 1:
						ans+=p+0.5;
						p=0;
						flag=2;
					break;
					case 2:
						ans+=p+1.0;
						p=0;
					break;
				}
			break;
		}
	if(p)
		switch(flag)
		{
			case 0:ans+=p-1.0;break;
			case 1:ans+=sqrt((p-0.5)*(p-0.5)+(7.0/4.0-sqrt(3)));break;
			case 2:
			{
				double x=1.0*(p);
				double y=(sqrt(3)/2.0-0.5);
				double z=sqrt(x*x+1.0-sqrt(3)/2.0);
				double len1=sqrt(x*x+1.0-sqrt(3)/2.0-0.25);
				double o=M_PI/2.0-atan(y/x)-acos(0.5/z);
				double len2=0.5*o;
				ans+=len1+len2;
			}
			break;
		}
	printf("%.9lf",ans);
	return 0;
}

---

rp++