Detecting Unstable Periodic Orbits in Chaotic Experimental Data （解析）

原文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.76.4705

发表在：PRL 1996

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

考虑一维的情况，假设map为f(x)， 我们的目标是去估计不动点x*=f(x*)。接下来，我们考虑下面的变换

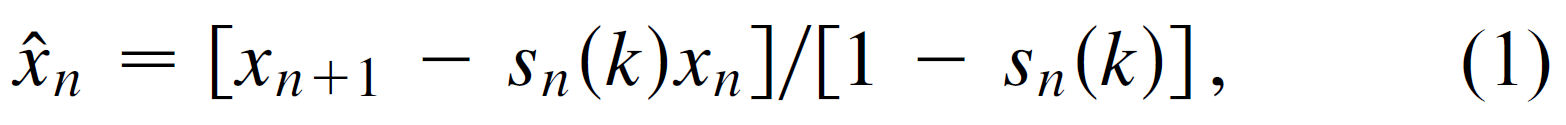
其中，

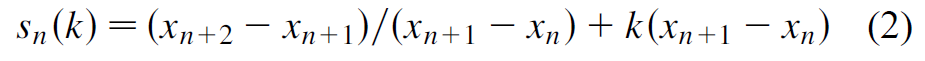
对于k=0的情况，我们可以有几何的解释，如下图，

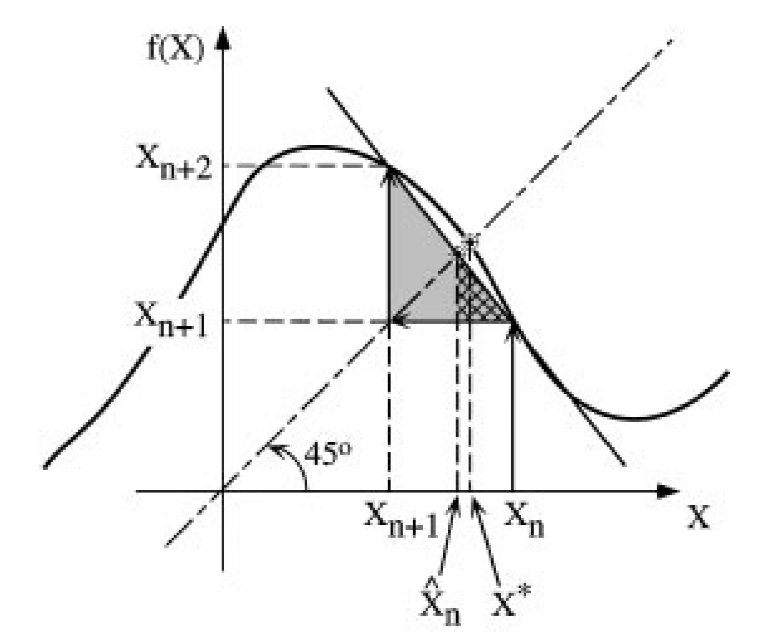
根据阴影的两个三角形的斜边的斜率关系可以得到下面的等式

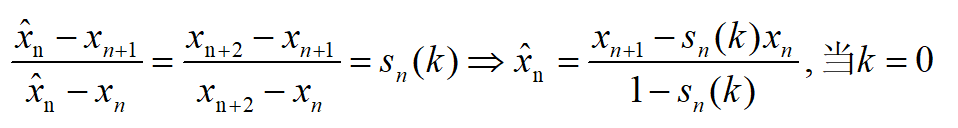
一个特例，当f(x)=x*+a(x-x*), 我们有

对于f(x)为一般的非线性函数以及k!=0,变换后的点都会集中在x*的线性区域的附近，并且我们可以证明变化后的点的密度函数有下面的关系，

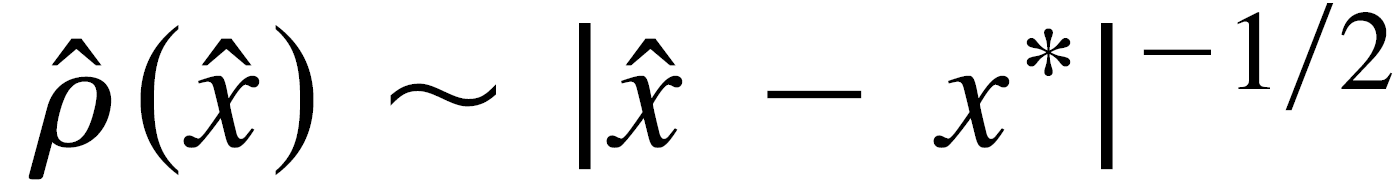
PS: 也就是说，变换后的点，在x*出，有奇异性，如果用有限的数据模拟，将会在x*出，出现一个sharp的峰.

下面简单推到下上面的密度函数。我们降变换的map重写写成下面的形式，

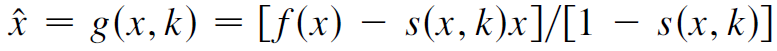
其中，

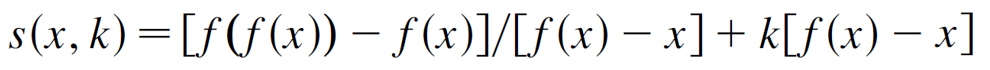
注意到，对于不动点x*，下面的等式于k是无关的

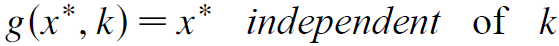
假设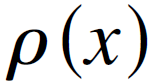为x的分布函数，那么我们有

其中,

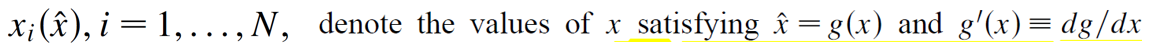
所以我们可以看到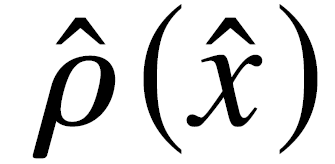出现奇异的地方在

　　1）的地方；

　　2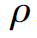）奇异的地方，

通过求g(x,k) 对于x的导数，我们发现，g'=0在不动点x*处 （i.e., f(x*)=x*。通过泰勒展开，我们有，

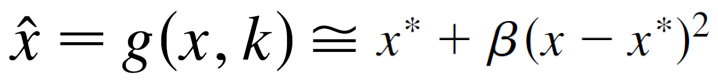
并且，

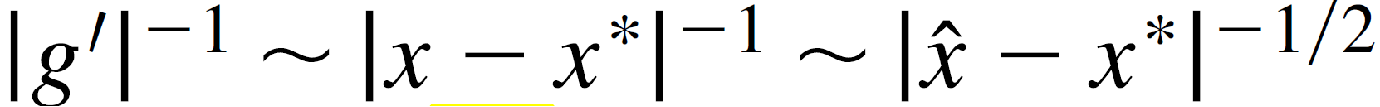
综上，我们得到，

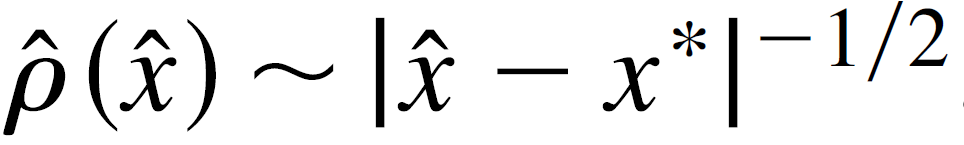
也就是说x*也是上面这个密度函数的奇异点，在这个奇异点，用有限数据进行模拟的时候，会有一个sharp的峰

但是，我们需要注意的是，上面说的sharp的峰，可能会是虚假的峰，i.e.， 不是由于fixed point引起的。因为虚假的峰，可能是由于

　　1）ρ(x)的奇异性

　　2）g'(x)=0

引起的,而x并非fixed point.

为了消除这些虚假的峰，我们注意到这些虚假的峰是于k的取值有关的。所以我们只需要取不同的k，然后平均，那么虚假的峰就会消除，而真实的峰就会保留。

Example

考虑logistic map

f(x)= ­ rx(1-x), r=3.092, k=0,

一共有4个sharp的峰，

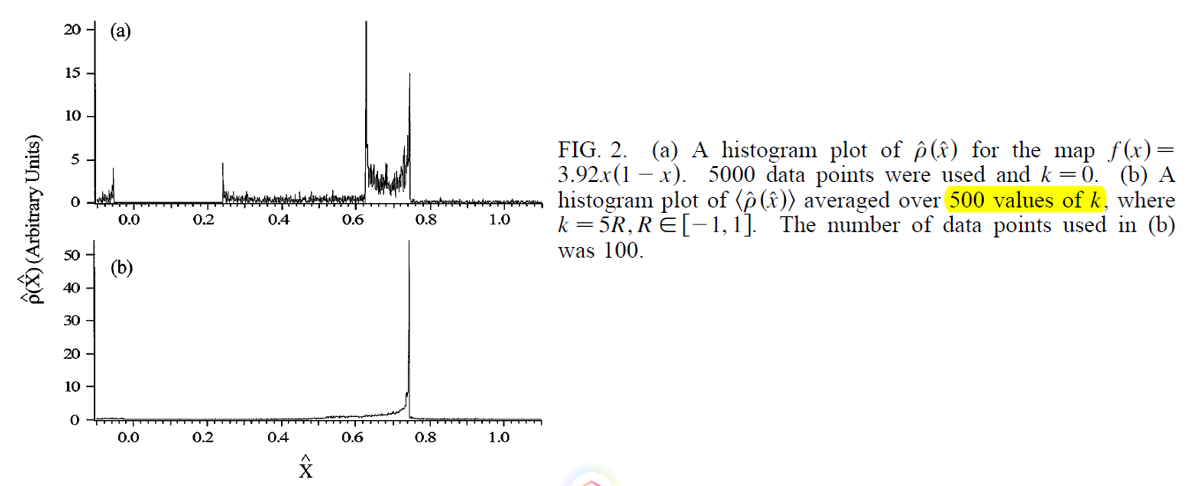
　　1）真实的峰，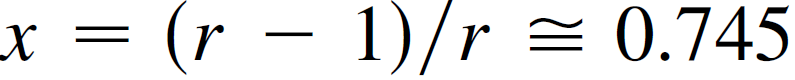

　　2）虚假的峰 -- ρ(x)的比较强的奇异性：  和

　　3）虚假的峰 -- g'为0的地方(不是fixed point)：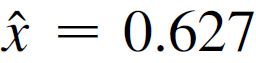 

 当k随机取500个值的时候，虚假的峰都消失了，真实的峰保留了。