AVLTree的实现以及左右旋转维持自平衡

AVL(Adelson-Velskii and Landis)树是带有平衡条件的二叉查找树。这个平衡条件必须要容易保持，而且它保证树的深度须是o(logN)。最简单的想法是要求左右子树具有相同的高度，这种想法并不要求树的深度要浅。

另一种平衡条件是要求每个节点都必须要有相同高度的左子树和右子树。通常空子树的高度定义为-1，只有具有(2^k)-1个节点的理想平衡树满足这个条件。因此，虽然这种平衡条件保证了树的深度小，但是它太严格而难以使用，需要放宽条件。

一棵AVL树是 其每个节点的左子树和右子树的高度最多差1的二叉查找树（空树高度为-1）。可以证明，初略地说，除去可能的插入外，所有的树操作都可以以时间O(logN)。当进行插入操作时，我们需要更新通向根节点路径上的那些节点的所有平衡信息，而插入操作隐含困难的原因在于，插入一个节点可能破坏AVL树的特性。如果发生这种情况，那么就要在考虑这一步插入完成之前回复平衡的性质。

在插入之后，只有那些从插入点到根节点的路径上的节点的平衡可能被改变，因为只有这些节点的子树可能发生变化。当我们沿着这条路径上行并更新平衡信息时，可以发现一个节点，它的新平衡破坏了AVL条件。我们将指出如何在第一个这样的节点（最深的节点）重新平衡这棵树，并证明这一重新平衡满足AVL性质。

我们把重新平衡的节点叫做a。由于任意节点最多有两个儿子，因此出现高度不平衡就需要a点的两棵子树的高度差2。容易看出，这种平衡可能出现在下面四种情况中：

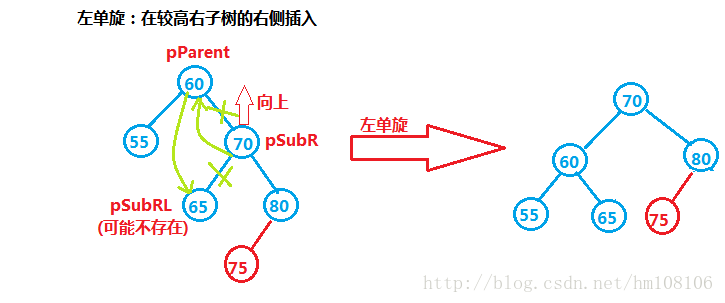
如上图的左旋转：

（1）我们把60当做70的左子节点

（2）并且把70的左子节点当做60的右子节点

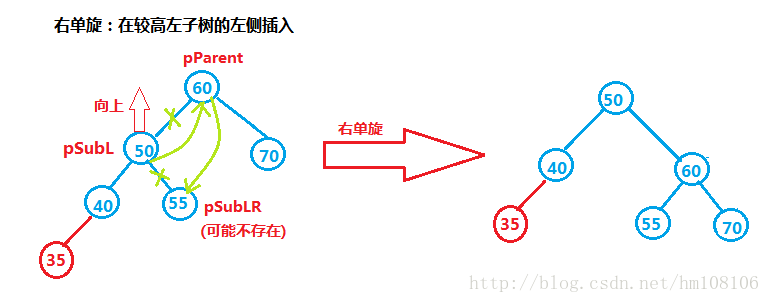
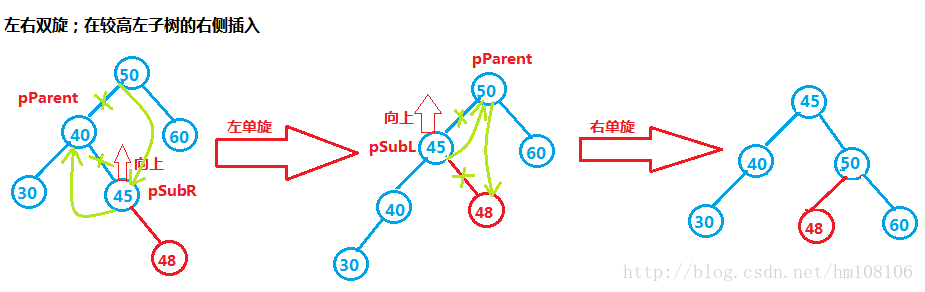
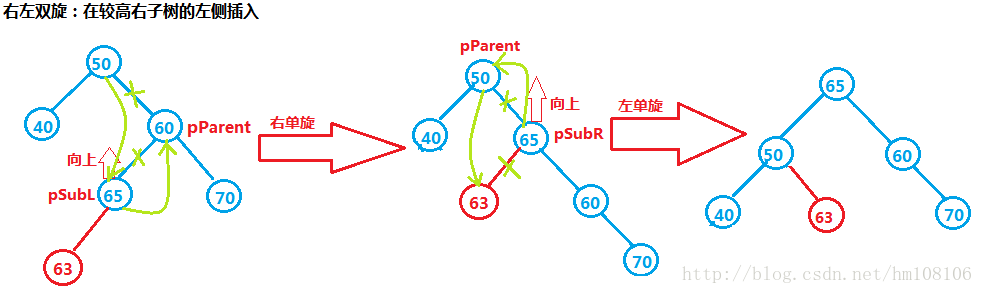
代码如下：

我们给出了添加元素和删除元素时，都要进行左右旋转自平衡的操作！

public class AVLTree<K extends Comparable<K>, V> {

	private class Node {
		public K key;
		public V value;
		public Node left, right;
		public int height;

		public Node(K key, V value) {
			this.key = key;
			this.value = value;
			left = null;
			right = null;
			height = 1;
		}
	}

	private Node root;
	private int size;

	public AVLTree() {
		root = null;
		size = 0;
	}

	public int getSize() {
		return size;
	}

	public boolean isEmpty() {
		return size == 0;
	}

	// 判断该二叉树是否是一棵二分搜索树
	public boolean isBST() {

		ArrayList<K> keys = new ArrayList<>();
		inOrder(root, keys);
		for (int i = 1; i < keys.size(); i++)
			if (keys.get(i - 1).compareTo(keys.get(i)) > 0)
				return false;
		return true;
	}

	private void inOrder(Node node, ArrayList<K> keys) {

		if (node == null)
			return;

		inOrder(node.left, keys);
		keys.add(node.key);
		inOrder(node.right, keys);
	}

	// 判断该二叉树是否是一棵平衡二叉树
	public boolean isBalanced() {
		return isBalanced(root);
	}

	// 判断以Node为根的二叉树是否是一棵平衡二叉树，递归算法
	private boolean isBalanced(Node node) {

		if (node == null)
			return true;

		int balanceFactor = getBalanceFactor(node);// 获取到当前节点的平衡因子
		if (Math.abs(balanceFactor) > 1)
			return false;
		return isBalanced(node.left) && isBalanced(node.right);
	}

	// 获得节点node的高度
	private int getHeight(Node node) {
		if (node == null)
			return 0;
		return node.height;
	}

	// 获得节点node的平衡因子
	private int getBalanceFactor(Node node) {
		if (node == null)
			return 0;
		return getHeight(node.left) - getHeight(node.right);
	}

	// 对节点y进行向右旋转操作，返回旋转后新的根节点x
    //        y                              x
    //       / \                           /   \
    //      x   T4     向右旋转 (y)        z     y
    //     / \       - - - - - - - ->    / \   / \
    //    z   T3                       T1  T2 T3 T4
    //   / \
    // T1   T2
	private Node rightRotate(Node y) {
		Node x = y.left;
		Node T3 = x.right;

		// 向右旋转过程
		x.right = y;
		y.left = T3;

		// 更新height
		y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
		x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

		return x;
	}

	// 对节点y进行向左旋转操作，返回旋转后新的根节点x
    //    y                             x
    //  /  \                          /   \
    // T1   x      向左旋转 (y)       y     z
    //     / \   - - - - - - - ->   / \   / \
    //   T2  z                     T1 T2 T3 T4
    //      / \
    //     T3 T4
	Node leftRotate(Node y) {
		Node x = y.right;
		Node T2 = x.left;

		// 向左旋转过程
		x.left = y;
		y.right = T2;

		// 更新height
		y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
		x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

		return x;
	}

	// 向二分搜索树中添加新的元素(key, value)
	public void add(K key, V value) {
		root = add(root, key, value);
	}

	// 向以node为根的二分搜索树中插入元素(key, value)，递归算法
	// 返回插入新节点后二分搜索树的根
	private Node add(Node node, K key, V value) {

		if (node == null) {
			size++;
			return new Node(key, value);
		}

		if (key.compareTo(node.key) < 0)
			node.left = add(node.left, key, value);
		else if (key.compareTo(node.key) > 0)
			node.right = add(node.right, key, value);
		else
			// key.compareTo(node.key) == 0
			node.value = value;

		// 更新height
		node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));

		// 计算平衡因子
		int balanceFactor = getBalanceFactor(node);

		if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0)
			// 左子树高度比右子树高度差大于1
			//           A                       A
			//         /                        /
			//       B        或者        B
			//     /                        /  \
			//   C                      C     D
			return rightRotate(node);

		if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0)
			// 右子树高度比左子树高度大1
			return leftRotate(node);

		if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
			node.left = leftRotate(node.left);
			return rightRotate(node);
		}

		if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
			node.right = rightRotate(node.right);
			return leftRotate(node);
		}

		return node;
	}

	// 返回以node为根节点的二分搜索树中，key所在的节点
	private Node getNode(Node node, K key) {

		if (node == null)
			return null;

		if (key.equals(node.key))
			return node;
		else if (key.compareTo(node.key) < 0)
			return getNode(node.left, key);
		else
			// if(key.compareTo(node.key) > 0)
			return getNode(node.right, key);
	}

	public boolean contains(K key) {
		return getNode(root, key) != null;
	}

	public V get(K key) {

		Node node = getNode(root, key);
		return node == null ? null : node.value;
	}

	public void set(K key, V newValue) {
		Node node = getNode(root, key);
		if (node == null)
			throw new IllegalArgumentException(key + " doesn't exist!");

		node.value = newValue;
	}

	// 返回以node为根的二分搜索树的最小值所在的节点
	private Node minimum(Node node) {
		if (node.left == null)
			return node;
		return minimum(node.left);
	}

	// 删除掉以node为根的二分搜索树中的最小节点
	// 返回删除节点后新的二分搜索树的根
	private Node removeMin(Node node) {

		if (node.left == null) {
			Node rightNode = node.right;
			node.right = null;
			size--;
			return rightNode;
		}

		node.left = removeMin(node.left);
		return node;
	}

	// 从二分搜索树中删除键为key的节点
	public V remove(K key) {

		Node node = getNode(root, key);
		if (node != null) {
			root = remove(root, key);
			return node.value;
		}
		return null;
	}

	private Node remove(Node node, K key) {

		if (node == null)
			return null;

		Node retNode;
		if (key.compareTo(node.key) < 0) {
			node.left = remove(node.left, key);
			// return node;
			retNode = node;
		} else if (key.compareTo(node.key) > 0) {
			node.right = remove(node.right, key);
			// return node;
			retNode = node;
		} else { // key.compareTo(node.key) == 0

			// 待删除节点左子树为空的情况
			if (node.left == null) {
				Node rightNode = node.right;
				node.right = null;
				size--;
				// return rightNode;
				retNode = rightNode;
			}

			// 待删除节点右子树为空的情况
			else if (node.right == null) {
				Node leftNode = node.left;
				node.left = null;
				size--;
				// return leftNode;
				retNode = leftNode;
			}

			// 待删除节点左右子树均不为空的情况
			else {
				// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
				// 用这个节点顶替待删除节点的位置
				Node successor = minimum(node.right);
				// successor.right = removeMin(node.right);
				successor.right = remove(node.right, successor.key);
				successor.left = node.left;

				node.left = node.right = null;

				// return successor;
				retNode = successor;
			}
		}

		if (retNode == null)
			return null;

		// 更新height
		retNode.height = 1 + Math.max(getHeight(retNode.left),
				getHeight(retNode.right));

		// 计算平衡因子
		int balanceFactor = getBalanceFactor(retNode);

		if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0)
			return rightRotate(retNode);

		if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0)
			return leftRotate(retNode);

		if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
			retNode.left = leftRotate(retNode.left);
			return rightRotate(retNode);
		}

		if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
			retNode.right = rightRotate(retNode.right);
			return leftRotate(retNode);
		}

		return retNode;
	}
}