机器学习降维--PCA

1.原理和概念

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。

PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。

PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。

其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。

可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。于是，可以忽略余下的坐标轴，

只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

如何得到这些包含最大差异性的主成分方向。通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值特征向量，选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。

这样就可以将数据矩阵转换到新的空间当中，实现数据特征的降维。由于得到协方差矩阵的特征值特征向量有两种方法：特征值分解协方差矩阵、奇异值分解协方差矩阵。

• 基于特征值分解协方差矩阵实现PCA算法
• 基于SVD分解协方差矩阵实现PCA算法

2协方差和散度矩阵

样本均值：

样本方差：

样本X和样本Y的协方差：

由上面的公式，得到以下结论：

(1) 方差的计算公式是针对一维特征，即针对同一特征不同样本的取值来进行计算得到；而协方差则必须要求至少满足二维特征；方差是协方差的特殊情况。

(2) 方差和协方差的除数是n-1,这是为了得到方差和协方差的无偏估计。

协方差为正时，说明X和Y是正相关关系；协方差为负时，说明X和Y是负相关关系；协方差为0时，说明X和Y是相互独立。

Cov(X,X)就是X的方差。当样本是n维数据时，它们的协方差实际上是协方差矩阵(对称方阵)。例如，对于3维数据(x,y,z)，计算它的协方差就是：

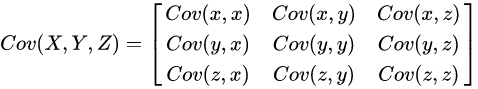
散布矩阵（散度矩阵）前乘以系数1/(n-1)就可以得到协方差矩阵：

关系：散度矩阵=类内离散度矩阵=类内离差阵=协方差矩阵×（n-1）

3 PCA算法两种实现方法

(1) 基于特征值分解协方差矩阵实现PCA算法

输入：数据集  ，需要降到k维。

1) 去平均值(即去中心化)，即每一位特征减去各自的平均值。

2) 计算协方差矩阵 ,注：这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。

3) 用特征值分解方法求协方差矩阵 的特征值与特征向量。

4) 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。

5) 将数据转换到k个特征向量构建的新空间中，即Y=PX。

总结：关于为什么用特征值分解矩阵，是因为  是方阵，能很轻松的求出特征值与特征向量。用奇异值分解也可以，是求特征值与特征向量的另一种方法。

举个例子：

以X为例，我们用PCA方法将这两行数据降到一行。

1)因为X矩阵的每行已经是零均值，所以不需要去平均值。

2)求协方差矩阵：

3)求协方差矩阵的特征值与特征向量。

求解后的特征值为： 　　　　　　　　　　其中对应的特征向量分别是一个通解，  和  可以取任意实数。那么标准化后的特征向量为：

                                       , 

4)矩阵P为：                                            5)最后我们用P的第一行乘以数据矩阵X，就得到了降维后的表示：

                 

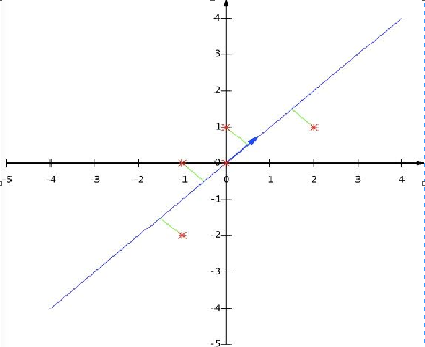
(2) 基于SVD分解协方差矩阵实现PCA算法

输入：数据集  ，需要降到k维。

1) 去平均值，即每一位特征减去各自的平均值。

2) 计算协方差矩阵。

3) 通过SVD计算协方差矩阵的特征值与特征向量。

4) 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。

5) 将数据转换到k个特征向量构建的新空间中。

在PCA降维中，需要找到样本协方差矩阵  的最大k个特征向量，然后用这最大的k个特征向量组成的矩阵来做低维投影降维。

在这个过程中需要先求出协方差矩阵 ,当样本数多、样本特征数也多的时候，这个计算还是很大的。当我们用到SVD分解协方差矩阵的时候，SVD有两个好处：

1) 有一些SVD的实现算法可以先不求出协方差矩阵  也能求出我们的右奇异矩阵V。也就是说，我们的PCA算法可以不用做特征分解而是通过SVD来完成，在样本量很大的时候很有效。

scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是特征值分解。

2)注意到PCA仅仅使用了我们SVD的左奇异矩阵，没有使用到右奇异值矩阵，那么右奇异值矩阵有什么用呢？

假设我们的样本是m*n的矩阵X，如果我们通过SVD找到了矩阵  最大的k个特征向量组成的k*n的矩阵  ,则我们可以做如下处理：

可以得到一个m*k的矩阵X',这个矩阵和我们原来m*n的矩阵X相比，列数从n减到了k，可见对列数进行了压缩。

也就是说，左奇异矩阵可以用于对行数的压缩；右奇异矩阵可以用于对列(即特征维度)的压缩。这就是用SVD分解协方差矩阵实现PCA可以得到两个方向的PCA降维(即行和列两个方向)。

4.

（1）PCA的Python实现：

##Python实现PCA
import numpy as np
def pca(X,k):#k is the components you want
  #mean of each feature
  n_samples, n_features = X.shape
  mean=np.array([np.mean(X[:,i]) for i in range(n_features)])
  #normalization
  norm_X=X-mean
  #scatter matrix
  scatter_matrix=np.dot(np.transpose(norm_X),norm_X)
  #Calculate the eigenvectors and eigenvalues
  eig_val, eig_vec = np.linalg.eig(scatter_matrix)
  eig_pairs = [(np.abs(eig_val[i]), eig_vec[:,i]) for i in range(n_features)]
  # sort eig_vec based on eig_val from highest to lowest
  eig_pairs.sort(reverse=True)
  # select the top k eig_vec
  feature=np.array([ele[1] for ele in eig_pairs[:k]])
  #get new data
  data=np.dot(norm_X,np.transpose(feature))
  return data

X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])

print(pca(X,1))

（2）用sklearn的PCA与我们的PCA做个比较：

##用sklearn的PCA
from sklearn.decomposition import PCA
import numpy as np
X = np.array([[-1, 1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca=PCA(n_components=1)
pca.fit(X)
print(pca.transform(X))

4. PCA的物理意义

PCA有两种通俗易懂的解释：(1)最大方差理论；(2)最小化降维造成的损失。这两个思路都能推导出同样的结果。

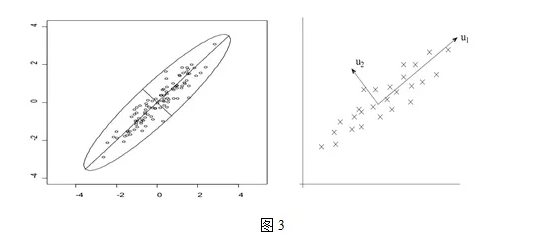
4.1  PCA算法优点

1，仅仅需要以方差衡量信息量，不受数据集以外的因素影响

2，各主成分之间正交，可消除原始数据成分间的相互影响的因素

3，计算方法简单，主要运算时特征值分解，易于实现

4.2  PCA算法缺点

1，主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强

2，方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响

5.维度K(主成分的个数) 调参实战