基于高斯分布的异常检测(Anomaly Detection)算法

记得在做电商运营初期，每每为我们频道的促销活动锁取得的“超高”销售额感动，但后来随着工作的深入，我越来越觉得这里面水很深。商家运营、品类运营不断的通过刷单来获取其所需，或是商品搜索排名，或是某种kpi指标，但这些所谓的“脏数据”，却妨碍了平台运营者对于真实数据的分析和促销效果的评估。今天我们讨论一种非监督学习算法(Unsupervised Learning Algorithm)，试图在真实数据中，找出并标注异常数据。

该算法是基于高斯分布的异常检测算法(Anomaly Detection Algorithm)，在很多场景中被广泛使用。其算法的核心思想是：给定一个m*n维训练集，将训练集转换为n为的高斯分布，通过对m个训练样例的分布分析，得出训练集的概率密度函数，即得出训练集在各个维度上的数学期望μ和方差σ^2，并且利用少量的Cross Validation集来确定一个阈值ε。当给定一个新的点，我们根据其在高斯分布上算出的概率，及阈值ε，判断当p<ε判定为异常，当p>ε判定为非异常。

该算法在一维下很好理解，而对于具有n维指标的训练样例来说，则稍微复杂。在二维情况下，训练样例分别分布于x1轴和x2轴，其概率密度函数可以用x1与x2确定的点，在三维空间中的高度来表征。如下图：

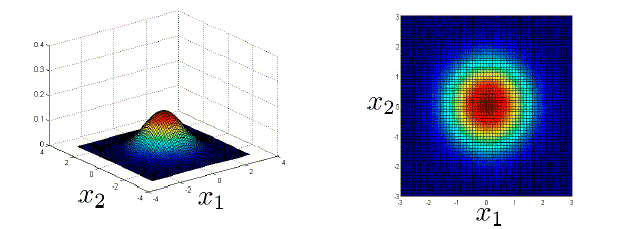
事实上，对于无偏移的n维高斯分布，其概率密度函数可以使用以下两种方式来表示：

概率式：

矩阵式：

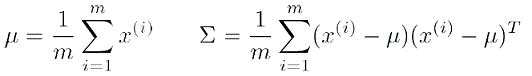
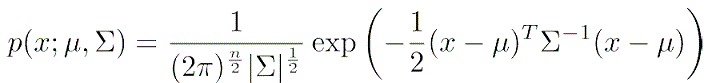
关于ε的确定，我们需要部分已知结果的训练样例作为CV集。在训练过程中，尝试多种ε的值，然后根据F1 Score来选择ε的值，其计算方式为：

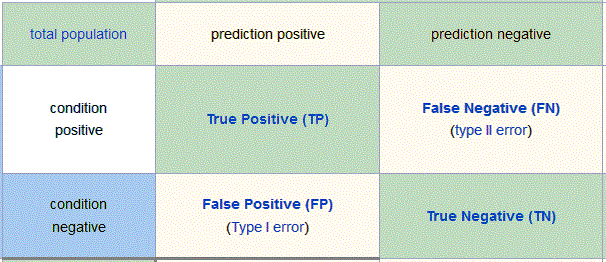
1、将预测与真实值的4种组合列出：预测为真且正确(TP)，预测为真且错误(TN)，预测为假且错误(FN)，预测为假且正确(TN)

2、计算准确率(precision=TP/(TP+FP))和召回率(recall=TP/(TP+FN));

3、计算F1:

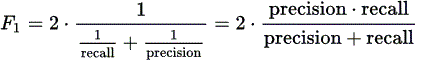
4、根据F1的最大值选择ε