机器学习五 EM 算法

引言
- 经典示例
EM算法
GMM 推导
参考文献:

引言

Expectation maximization (EM) 算法是一种非常神奇而强大的算法. EM算法于 1977年由Dempster 等总结提出. 说EM算法神奇而强大是因为它可以解决含有隐变量的概率模型问题.

EM算法是一个简单而又复杂的算法. 说它简单是因为其操作过程就两步, E(expectation)步: 求期望; M(maximization)步, 求极大. 说它复杂,是因为刚刚学习的时候,你会发现EM算法并不像之前的算法那么的直观, 而且推导过程的tricks 理解起来也颇费精力. 不过,所谓'来者如临高山,往者如观逝水.' You can do IT!

经典示例

EM算法有一些非常经典的例子, 比如'硬币问题','小球问题','男女同学身高问题'等等. 比如硬币问题: 有A, B, C三枚硬币, 这些硬币掷出正面的概率分别为 $\pi$, p, q. 先掷A硬币, 根据其结果选择掷B, 还是C. 然后投掷所选硬币, 投掷结果,正面记 1, 反面记 0. 独立地重复 n 次试验,比如最终结果是 1,0,1,1,0,1,0,0,1,0,0,1,0,1,1,0,0,1,1,1 (也即 n = 20). 那么问 $\pi$, p, q分别是多少?

'小球问题'类似, 咱们介绍下'男女身高问题': 某大学进行体检, 每位同学的身高都记录下来:1.72, 1.58, 1.67, 1.89, …, 然后只根据身高数据(也即不知道某一身高数据(如 1.67)是来男同学还是女同学) 推测出这个学校学生的男女比例, 及男, 女同学各自的概率分布(假设均服从高斯分布).

怎么样, 有思路吗? 是不是这些看似简单的问题而又接近生活的问题, 其实并不太好解决?

我和一样, 在没有邂逅EM算法时, 也只能望洋兴叹.

EM算法

设样本数据: $\{x_1, x_2, \dots,x_n\}$ ,相互独立; 样的隐变量为 Z: $\{z_1,z_2,\dots,z_m\}$, 现在求出样本空间每个数据的隐变量, 及每个隐变量(也可能是连续的)相关的分布参数$\theta$.

这个需要解释下, 也就是说,对于一组观测数据, 其背的隐变量是怎样的情况(比如有一个数据1.72, 这个身高是男同学的还是女同学的(男,女就是陷变量)? 其概率分别是多少? 二者的比比例呢?)

在没有隐变量, 变隐变量已知的情况下, 求概率分布($\theta$) 最常用, 最方便的方法就是最大似然估计(maximization likelihood estimation, MLE):
\[
L(\theta) = \Pi_{i = 1}^n p(x_i, \theta)
\]
或者对数形式:
\[
l(\theta) = \sum_{i=1}^n\log p(x_i,\theta)
\]
但当隐变量存在且未知时, 那这个问题就复杂了:
\[
l(z,\theta) = \sum_{i=1}^n\log p(x_i,z,\theta)
\]
因为隐变量 z 未知, 所以求解参数$\theta$ 就变得困难了, 就算要求 z 参数 $\theta$ 未知, 也不太好求解.

EM 算法就是为解决此问题而生的. EM 算法最终应用的也是MLE, 而MLE不能正常实施的根本原因就是隐变量未知, 如果隐变量已知了, 问题就解决了. 那如何让隐变量'已知'呢? 加'先验'啊. 我根据先验知识给出情况隐变量的,那参数 $\theta$ 就可以求出来了. 当然这样的先验误差会很大的. 当我们求出参数后, 参数就算已知了, 反过来就可以推导出更'准确'的隐变量了. 这样如此往复, 隐变量, 参数相互作用, 最终就可得出的结果了.

既然是MLE, 那还是要:
\[
\max_{z ,\theta} l(z,\theta)
\]
其中
\[
\begin{array}
\\
l(z,\theta)& = & \sum_{i=1}^n\log p(x_i,z,\theta)\\
&=& \sum_{i=1}^n \log \sum_{j = 1}^m p(x_i,z_j,\theta)\\
&=& \sum_{i =1}^n \log\sum_{j = 1}^m Q_i(z_j)\frac{p(x_i,z_j,\theta)}{Q_i(z_j)}\\
\end{array}
\]
上式第一步应用的是全概率公式, 第二步 $Q(z)$ 是 z 的某种分布, 说是'某种' 是因为为了给出隐变量的先验, 至少需要把隐变量的分布表示出来(或剥离出来). 既然是某种分布, 则:
\[
\sum_{j = 1}^m Q_i(z_j) =1
\]
接下来用到的一个知识是Jensen不等式(Jensen Inequality):

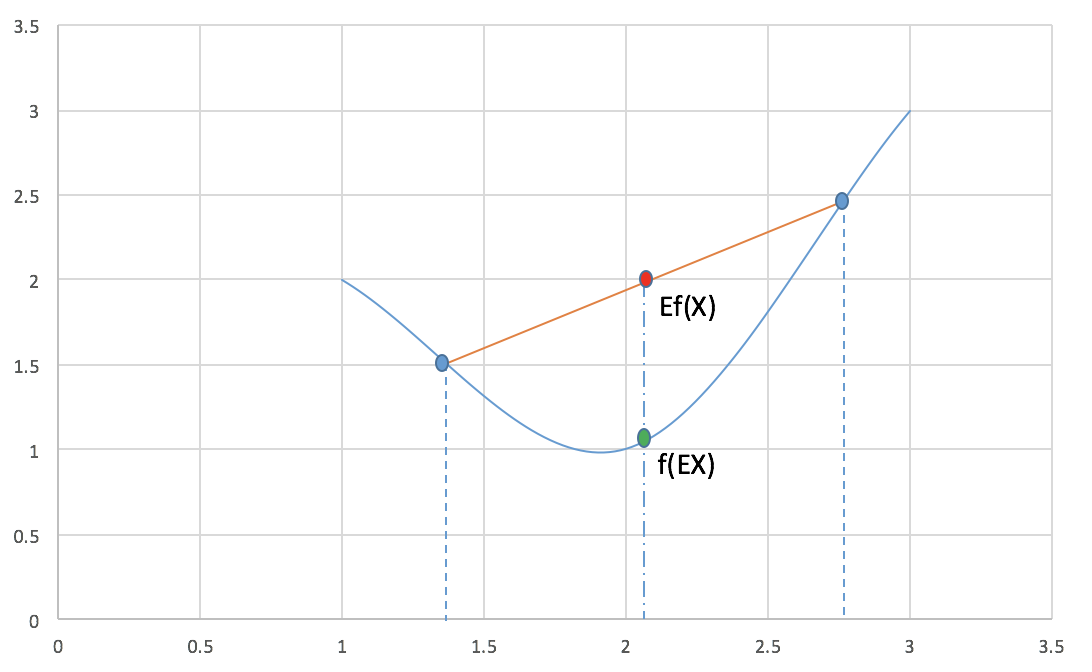
对于凸函数 f 有:
\[
E[f(X)] \ge f(EX)
\]
其中X 是随机变量. 下面这张图很好的展示了此等关系.

现在再看下(5)式, 你会发现:
\[
\begin{array}\\
l(z,\theta) &=& \sum_{i =1}^n \log\sum_{j = 1}^m Q_i(z_j)\frac{p(x_i,z_i,\theta)}{Q_i(z_j)}\\
& \ge & \sum_{i =1}^n\sum_{j = 1}^m Q_i(z_j) \log\frac{p(x_i,z_j,\theta)}{Q_i(z_j)}\\
\end{array}
\]
上式可以看作是对$l(z,\theta)$ 求下界, 而这个下界一定程度上取决于$Q(z_j)$, $\frac{p(x_i,z_i,\theta)}{Q(z_j)}$, 也就是说, 我们可以调整此二者使这个下界尽可能的大, 也就尽可能的接近$l(z, \theta)$, 这个下界最大才可能等于$l(z, \theta)$, 这也是取等号的条件. 换句话说, 什么情况下取等号? 根据 Jensen 不等式, 只有当$\frac{p(x_i,z_i,\theta)}{Q(z_j)}$为定值时才可以(为定值,以上图为例,也就是$x_1, x_2$ (图上两蓝色点)相等, 也就是非常非常''接近'',最终成为同一个点了.). 也就是说, 无论如何无论如何调整z 隐变量, 这个值都不会变化了(都是同一个某点), 不妨设为 c:
\[
\frac{p(x_i,z_j,\theta)}{Q_i(z_j)} = c
\]
由(6),(9)式,消去 c 可得:
\[
Q_i(z_j)=\frac{p(x_i,z_j,\theta)}{\sum_{j= 1}^m p(x_i,z_j,\theta)} = \frac{p(x_i,z_j,\theta)}{p(x_i,\theta)} = p(z_j|x_i)
\]
终于知道了, 所谓的隐变量的'某'种分布就是已知数据观测值时隐变量的条件概率.

这样 EM算法就基本'搞定'隐变量了, 那么EM算法(变了形的MLE)的基本步骤:

E步:
\[
Q_i(z_j)=\frac{p(x_i,z_j,\theta)}{\sum_{j= 1}^m p(x_i,z_j,\theta)} = p(z_j|x_i),\\ i = 1,2,\dots,n,\quad j = 1,2,\dots,m
\]
M步: 求MLE:

\[
\max_\theta l= \sum_{i =1}^n\sum_{j = 1}^m Q_i(z_j) \log\frac{p(x_i,z_j,\theta)}{Q_i(z_j)}
\]

GMM 推导

对于学生身高问题, 是经典的高斯混合模型(Gaussian Mixed Model, GMM). 设随机变量 X 是由 k 个高斯分布混合而成, 各个高斯分布的概率分别为$\psi_1,\psi_2,\dots,\psi_k$, 且第 i 个分布的均值方差为 ($\mu_i, \sigma_i$). 现在的要求是已知一系列样本$x_1, x_2, \dots,x_n$, 试估计 $\psi, u,\sigma$.

仍然, 我们的方式还是最大化下式:
\[
l(\theta) = \sum_{i = 1}^n\log p(x_i,z,\theta) =\sum_{i=1}^n \log \sum_{j = 1}^k p(x_i,z_j,\theta)
\]
这里的隐变量即是分布类似别了(即哪个高斯分布, j 取 (1,…,k)的哪个).

因为推出公式了, 直接代入就可以了:

第一步(E步):
\[
Q_i(z_j) = p(z_j|x_i,\theta) = p(z_j|x_i,\psi, u,\sigma)=\frac{p(x_i,z_j,\theta)}{\sum_{j= 1}^m p(x_i,z_j,\theta)}
\]
第二步(M步):
\[
\max l(\theta) = \max \sum_{i=1}^n \sum_{j = 1}^k Q_i(z_j)\log\frac{p(x_i,z_j,\theta)}{Q_i(z_j)}
\]
因为是高斯分布,所以p的形式:
\[
p(x_i,z_j,\theta) = p(x_i,z_j,\mu_j,\sigma_j) = \frac{1}{\sqrt{2\pi \sigma_j}}\exp(-\frac{1}{2\sigma_j^2}(x_i - \mu_j)^2) \cdot \psi_j
\]
代入(15)式:
\[
\begin{array}\\
\max l(\mu,\sigma) &=& \max_{\theta} \sum_{i=1}^n \sum_{j = 1}^k Q_i(z_j)\log\frac{\frac{1}{\sqrt{2\pi \sigma_j}}\exp(-\frac{1}{2\sigma_j^2}(x_i - \mu_j)^2) \cdot \psi_j}{Q_i(z_j)}\\
&=& \max_{\theta} \sum_{i=1}^n \sum_{j = 1}^k Q_i(z_j)((-\frac{1}{2}\log(2\pi\sigma_j) \\
&&\qquad-\frac{1}{2\sigma_j^2}(x_i - \mu_j)^2 + \log\psi_j- \log(Q_i(z_j))\\
\end{array}
\]
对上式中的$\mu,\sigma$ 分别求导即可得出结果:
\[
\begin{array}\\
\frac{\partial l(\mu_j)}{\partial \mu_j} &=& \sum_{i=1}^n Q_i(z_j)\cdot(-\frac{(x-\mu_j)}{\sigma_j}) = 0\\
&==>& \mu_j = \frac{\sum_{i=1}^n Q_i(z_j)x_i}{\sum_{i =1}^nQ_i(z_j)}
\end{array}
\]
同理:
\[
\sigma_j = \frac{\sum_{i =1}^nQ_i(z_j) (x_j - \mu_j)^2}{\sum_{j = 1}^mQ_i(z_j)}
\]
对于 $\psi$ 的求解稍微麻烦些, 不过也很自然, 因$\psi $ 有如下约束:
\[
\sum_{j = 1}^k \psi_k = 1
\]
因此要与(17)式构建Lagrange 方程:
\[
\mathscr{L(\psi)} = l(\psi)+ \lambda(\sum_{j=1}^k\psi_j - 1)
\]
对$\psi_j$ 求导即可得到:
\[
\psi_j = \frac{1}{n}\sum_{i=1}^nQ_i(z_j)
\]
对于硬币问题, 只需把上面的高斯分布换成Bernoulli 分布即可.

参考文献:

统计学习方法, 李航, 2012, 清华大学出版社;
Pattern Recognition and Machine learning, Christopher M. Bishop, 2006, Springer;
The EM algorithm, JerryLead, 2011, cnblogs;