[CSP-S模拟测试]:marshland（最大费用可行流）

题目描述

前方有一片沼泽地。
方便地，我们用一个$n\times n$的网格图来描述它，每一个格子代表着沼泽地的一小片区域。其中$(1,1)$代表网格图的左上角，$(n,n)$代表网格图的右下角。若用$X$表示行数，$Y$表示列数，那么$X+Y$为奇数的格子有一个危险度为$0$。
为了保障人们的安全，你有$m$个长相怪异的大石头，你可以选一些石头放在网格图上的某些格子，石头可以看成一个$'L'$形的块，并且占三个格子，它通过旋转有四种方式供放置，仅会使得在拐角处的那个格子危险度减为$0$。
网格图中还有$k$个位置是“禁止位置”，石头的任何部位都不能位于这些格子上，且这些位置的危险度一定为$0$。
现在你需要知道放置一些石头之后最小危险度之和是多少。（石头可以不放完）

---

输入格式

第一行三个整数$n,m,k$。
接下来$n$行每行$n$个整数，表示每个格子的危险读，保证$X+Y$为偶数的格子和禁止位置的格子的危险度为$0$。
接下来$k$行每行$2$个整数$X,Y$，表示禁止位置的坐标，注意可能会出现重复的禁止位置。

---

输出格式

输出一行一个整数代表最小的危险度之和。

---

样例

样例输入1：

3 3 1
0 1 0
2 0 1
0 1 0
1 3

样例输出1：

3

样例输入2：

3 3 4
0 2 0
0 0 4
0 3 0
1 3
2 1
2 2
3 1

样例输出2：

9

---

数据范围与提示

对于$10\%$的数据，满足$n\leqslant 4$。
对于$30\%$的数据，满足$n\leqslant 10$。
对于$100\%$的数据，满足$n\leqslant 50$。
对于所有数据，满足$0\leqslant m\leqslant \frac{n^2}{3},0\leqslant k\leqslant n^2,0\leqslant V_{x,y}\leqslant {10}^6$。

---

题解

在坐的各位应该都能看出来大石头的拐角一定压住有危险度的点了叭？为什么我也不赘述了，这要是都想不出来尽早退役。

$0\%$算法：

乍一看你可能会觉得是道$DP$，设$dp[i][j][0/1][0/1/2/3]$表示在$(i,j)$有没有放石头，放了的话朝向是哪儿的最小危险度，看似简单，打起来瞬间见祖宗。

于是弃掉这种做法，事实证明我打了$150+$行的状态转移一分没拿。

有的时候假的贪心是能在关键时刻出奇迹的，比方说着道题。

我们先把所有格子的危险度从小到大排名，然后依次覆盖，可以覆盖就覆盖，不可以就跳过。

为了提高正确率，我们在覆盖当前格子的同时也要考虑一下其它的格子，比方说下面这张图，我们在覆盖红色格子的同时可能会影响到蓝色格子：

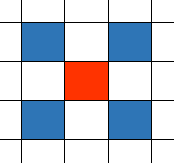
那么我们可以考虑将蓝色格子再比较大小，然后朝危险度最小的那个格子的方向放置：

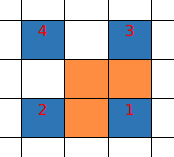
这种贪心思想大大提高了正确率，但是它依然是不正确的，比方说你可能放置了一块石头压住了一个危险度较大的格子，但是却使好多危险度较小的格子被阻碍放置。

时间复杂度：$\Theta(n^2)$。

期望得分：$0$分。

实际得分：$40$分。

$100\%$算法：

对于卓越的我们，当然不能只是止步于上面那个假的贪心啦（虽说考场上我也就是交了上面那个假的贪心……）

那么考虑正解，偷偷看一眼数据范围，$n$好小，所以我们可以考虑网络流（我也不知道为什么就一定要考虑网络流），在筛选一番之后发现这是一个最大费用可行流，那么怎么连边呢？

认真观察之后发现，一个$L$是由一个$X+Y$为奇数和两个$X+Y$为偶数的点组成，那也不够哇？在认真观察，发现$X+Y$为偶数的那两个点一定是由一个为奇$+$奇，一个为偶$+$偶组成的，所以将有危险度的点连边，并将$L$的剩下两个点连边向源点和汇点即可，对于这道题建议使用$EK$，下面的标程使用的也是$EK$。

我的做法是每次只流一个，代码复杂度比较低，但是速度并没有优势。

在注意一下流量是$m$即可。

时间复杂度：$\Theta(n^4)$（也许是吧，我也不太会算……）

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

$40$分假贪心：

#include<bits/stdc++.h>
using namespace std;
struct rec
{
	int x,y,w;
}e[50000];
int n,m,k;
int cnt;
int Map[100][2500];
bool vis[100][2500];
long long ans,sum;
bool cmp(rec a,rec b){return a.w>b.w;}
int main()
{
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		{
			scanf("%d",&Map[i][j]);
			if(Map[i][j])
			{
				e[++cnt].x=i;
				e[cnt].y=j;
				e[cnt].w=Map[i][j];
				ans+=Map[i][j];
			}
		}
	sort(e+1,e+cnt+1,cmp);
	while(k--)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		vis[x][y]=1;
	}
	for(int i=0;i<=n+1;i++)vis[i][0]=vis[i][n+1]=1;
	for(int i=0;i<=n+1;i++)vis[0][i]=vis[n+1][i]=1;
	for(int i=1;i<=cnt&&m;i++)
	{
		int x=e[i].x;
		int y=e[i].y;
		int w=e[i].w;
		int m1=Map[x-1][y-1];
		int m2=Map[x-1][y+1];
		int m3=Map[x+1][y-1];
		int m4=Map[x+1][y+1];
		if(!vis[x-1][y]&&!vis[x][y-1]&&!vis[x+1][y]&&!vis[x][y+1])
		{
			sum+=w;
			m--;
			vis[x][y]=1;
			if(m1<=m2&&m1<=m3&&m1<=m4){vis[x-1][y]=vis[x][y-1]=1;continue;}
			if(m2<=m1&&m2<=m3&&m2<=m4){vis[x-1][y]=vis[x][y+1]=1;continue;}
			if(m3<=m1&&m3<=m2&&m3<=m4){vis[x+1][y]=vis[x][y-1]=1;continue;}
			if(m4<=m1&&m4<=m2&&m4<=m3){vis[x+1][y]=vis[x][y+1]=1;continue;}
		}
		if(!vis[x][y-1]&&!vis[x+1][y]&&!vis[x][y+1])
		{
			sum+=w;
			m--;
			vis[x][y]=vis[x+1][y]=1;
			if(m3<=m4){vis[x][y-1]=1;continue;}
			else {vis[x][y+1]=1;continue;}
		}
		if(!vis[x-1][y]&&!vis[x+1][y]&&!vis[x][y+1])
		{
			sum+=w;
			m--;
			vis[x][y]=vis[x][y+1]=1;
			if(m2<=m4){vis[x-1][y]=1;continue;}
			else {vis[x+1][y]=1;continue;}
		}
		if(!vis[x-1][y]&&!vis[x][y-1]&&!vis[x][y+1])
		{
			sum+=w;
			m--;
			vis[x][y]=vis[x-1][y]=1;
			if(m1<=m2){vis[x][y-1]=1;continue;}
			else {vis[x][y+1]=1;continue;}
		}
		if(!vis[x-1][y]&&!vis[x][y-1]&&!vis[x+1][y])
		{
			sum+=w;
			m--;
			vis[x][y]=vis[x][y-1]=1;
			if(m1<=m3){vis[x-1][y]=1;continue;}
			else {vis[x+1][y]=1;continue;}
		}
		if(!vis[x-1][y]&&!vis[x][y-1])
		{
			sum+=w;
			m--;
			vis[x][y]=vis[x-1][y]=vis[x][y-1]=1;
			continue;
		}
		if(!vis[x-1][y]&&!vis[x][y+1])
		{
			sum+=w;
			m--;
			vis[x][y]=vis[x-1][y]=vis[x][y+1]=1;
			continue;
		}
		if(!vis[x+1][y]&&!vis[x][y-1])
		{
			sum+=w;
			m--;
			vis[x][y]=vis[x+1][y]=vis[x][y-1]=1;
			continue;
		}
		if(!vis[x+1][y]&&!vis[x][y+1])
		{
			sum+=w;
			m--;
			vis[x][y]=vis[x+1][y]=vis[x][y+1]=1;
			continue;
		}
	}
	cout<<ans-sum<<endl;
	return 0;
}

$100\%$算法：

#include<bits/stdc++.h>
using namespace std;
struct rec
{
	int nxt;
	int to;
	int w;
}e[1000000];
int head[5000],cnt;
int n,m,k;
int tot=2;
int Map[51][51];
bool vis[51][51];
int S[51][51],T[51][51];
int que[1000000],dis[1000000],g[1000000];
int dp[5000][5000],wzc[51][51],c[5000][5000];
bool v[1000000];
int ans;
void add(int x,int y,int w)
{
	e[++cnt].nxt=head[x];
	e[cnt].to=y;
	e[cnt].w=w;
	head[x]=cnt;
}
bool bfs()
{
	for(int i=1;i<=tot;i++)
	{
		dis[i]=-20020923;
		g[i]=v[i]=0;
	}
	dis[1]=0;
	v[1]=1;
	int he=1,ta=1;
	que[ta]=1;
	while(he<=ta)
	{
		for(int i=head[que[he]];i;i=e[i].nxt)
			if(dp[que[he]][e[i].to]&&dis[que[he]]+c[que[he]][e[i].to]>dis[e[i].to])
			{
				dis[e[i].to]=dis[que[he]]+c[que[he]][e[i].to];
				g[e[i].to]=que[he];
				if(!v[e[i].to])
				{
					v[e[i].to]=1;
					que[++ta]=e[i].to;
				}
			}
		v[que[he]]=0;
		he++;
	}
	return dis[2]>0;
}
int main()
{
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		{
			scanf("%d",&Map[i][j]);
			ans+=Map[i][j];
		}
	while(k--)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		vis[x][y]=1;
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(Map[i][j])
			{
				S[i][j]=++tot;
				T[i][j]=++tot;
				add(tot-1,tot,Map[i][j]);
				add(tot,tot-1,Map[i][j]);
				c[tot-1][tot]=Map[i][j];
				c[tot][tot-1]=-Map[i][j];
				dp[tot-1][tot]++;
			}
			else if(!vis[i][j]&&!((i+j)&1))
			{
				wzc[i][j]=++tot;
				if(i&1)
				{
					add(1,tot,0);
					add(tot,1,0);
					dp[1][tot]++;
				}
				else
				{
					add(tot,2,0);
					add(2,tot,0);
					dp[tot][2]++;
				}
			}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(Map[i][j])
			{
				if(i-1>0&&!vis[i-1][j])
				{
					if((i-1)&1)
					{
						add(wzc[i-1][j],S[i][j],0);
						add(S[i][j],wzc[i-1][j],0);
						dp[wzc[i-1][j]][S[i][j]]++;
					}
					else
					{
						add(T[i][j],wzc[i-1][j],0);
						add(wzc[i-1][j],T[i][j],0);
						dp[T[i][j]][wzc[i-1][j]]++;
					}
				}
				if(j-1>0&&!vis[i][j-1])
				{
					if(i&1)
					{
						add(wzc[i][j-1],S[i][j],0);
						add(S[i][j],wzc[i][j-1],0);
						dp[wzc[i][j-1]][S[i][j]]++;
					}
					else
					{
						add(T[i][j],wzc[i][j-1],0);
						add(wzc[i][j-1],T[i][j],0);
						dp[T[i][j]][wzc[i][j-1]]++;
					}
				}
				if(i+1<=n&&!vis[i+1][j])
				{
					if((i+1)&1)
					{
						add(wzc[i+1][j],S[i][j],0);
						add(S[i][j],wzc[i+1][j],0);
						dp[wzc[i+1][j]][S[i][j]]++;
					}
					else
					{
						add(T[i][j],wzc[i+1][j],0);
						add(wzc[i+1][j],T[i][j],0);
						dp[T[i][j]][wzc[i+1][j]]++;
					}
				}
				if(j+1<=n&&!vis[i][j+1])
				{
					if(i&1)
					{
						add(wzc[i][j+1],S[i][j],0);
						add(S[i][j],wzc[i][j+1],0);
						dp[wzc[i][j+1]][S[i][j]]++;
					}
					else
					{
						add(T[i][j],wzc[i][j+1],0);
						add(wzc[i][j+1],T[i][j],0);
						dp[T[i][j]][wzc[i][j+1]]++;
					}
				}
			}
	k=0;
	while(k<m&&bfs())
	{
		int flag=2;
		while(g[flag])
		{
			ans-=c[g[flag]][flag];
			dp[g[flag]][flag]--;
			dp[flag][g[flag]]++;
			flag=g[flag];
		}
		k++;
	}
	cout<<ans<<endl;
	return 0;
}

---

rp++