左闭右开线段树 2019牛客多校（第七场）E_Find the median（点代表区间

@

目录

• 题意
• 一种解析
• AC_Code

题意

链接：here

我理解的题意就是：初始序列为空，有\(n(400000)\)次操作，每次操作把区间\([Li,Ri]\)的数字加进序列，序列自动有序，每次操作后输出中位数是多大。

感觉赛时想的方法应该也是可以写的，很有道理可能会麻烦一点，大概就是二分答案再瞎搞一下。。

一种解析

一个套路：左闭右开线段树

还是很像权值线段树，不过叶子节点代表的不是一个点的值了，而是代表这个区间值域的情况。

添加了\(n\)个值域区间，他们会将这个大的值域切割成很多部分。显然添加\([Li,Ri]\)这个值域时，可以分解成添加了很多段值域区间。

把每个点都当成一个左闭右开的区间，把所有的\(Li,Ri+1\)离散化下来。

然后更新就是做一个区间加法的操作，一个点加了一次表示它代表的区间每个值都出现了一次。

查询就和普通权值线段树查询一样。查到叶子节点是，先算出这个区间每个值出现的次数\(len\)，已知我要找排在第\(p\)位的数，这个点代表值域的左端点是\(L\)，那么答案就是：\((p+len-1)/len+L-1\)。

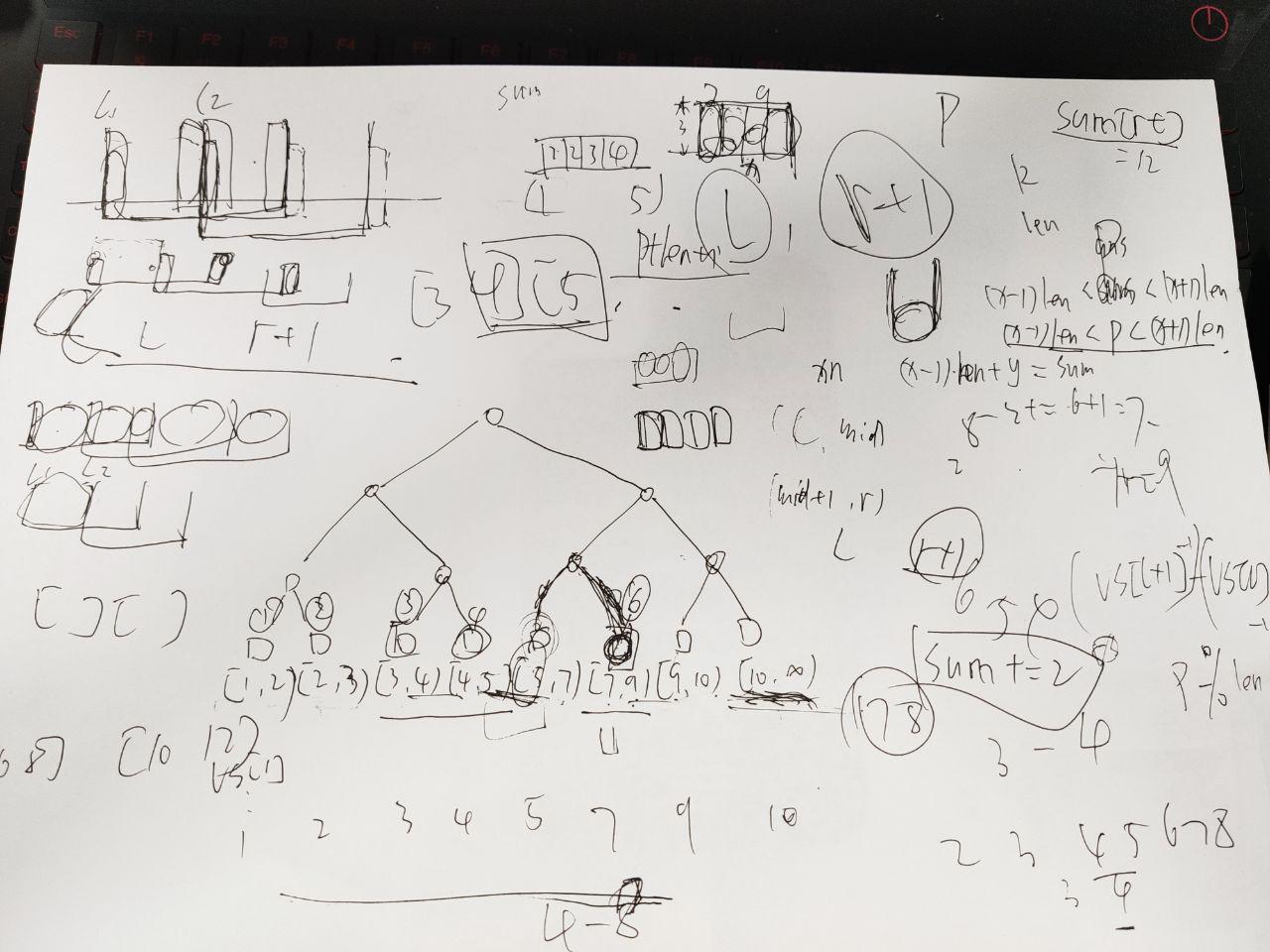
AC_Code

#pragma comment(linker, "/STACK:102400000,102400000")
//#include<bits/stdc++.h>
#include <ctime>
#include <iostream>
#include <assert.h>
#include <vector>
#include <queue>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define fi first
#define se second
#define endl '\n'
#define o2(x) (x)*(x)
#define BASE_MAX 31
#define mk make_pair
#define eb push_back
#define SZ(x) ((int)(x).size())
#define all(x) (x).begin(), (x).end()
#define clr(a, b) memset((a),(b),sizeof((a)))
#define iis std::ios::sync_with_stdio(false); cin.tie(0)
#define my_unique(x) sort(all(x)),x.erase(unique(all(x)),x.end())
using namespace std;
#pragma optimize("-O3")
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> pii;
inline LL read() {
    LL x = 0;int f = 0;
    char ch = getchar();
    while (ch < '0' || ch > '9') f |= (ch == '-'), ch = getchar();
    while (ch >= '0' && ch <= '9') x = (x << 3) + (x << 1) + ch - '0', ch = getchar();
    return x = f ? -x : x;
}
inline void write(LL x, bool f) {
    if (x == 0) {putchar('0'); if(f)putchar('\n');else putchar(' ');return;}
    if (x < 0) {putchar('-');x = -x;}
    static char s[23];
    int l = 0;
    while (x != 0)s[l++] = x % 10 + 48, x /= 10;
    while (l)putchar(s[--l]);
    if(f)putchar('\n');else putchar(' ');
}
int lowbit(int x) { return x & (-x); }
template<class T>T big(const T &a1, const T &a2) { return a1 > a2 ? a1 : a2; }
template<class T>T sml(const T &a1, const T &a2) { return a1 < a2 ? a1 : a2; }
template<typename T, typename ...R>T big(const T &f, const R &...r) { return big(f, big(r...)); }
template<typename T, typename ...R>T sml(const T &f, const R &...r) { return sml(f, sml(r...)); }
void debug_out() { cerr << '\n'; }
template<typename T, typename ...R>void debug_out(const T &f, const R &...r) {cerr << f << " ";debug_out(r...);}
#define debug(...) cerr << "[" << #__VA_ARGS__ << "]: ", debug_out(__VA_ARGS__);

const LL INFLL = 0x3f3f3f3f3f3f3f3fLL;
const int HMOD[] = {1000000009, 1004535809};
const LL BASE[] = {1572872831, 1971536491};
const int mod = 1e9 + 0;//998244353
const int MOD = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int MXN = 1e6 + 7;
const int MXE = 1e6 + 7;

int n, m;
int xs[MXN], ys[MXN], ls[MXN], rs[MXN];
LL a1, a2, b1, b2, c1, c2, m1, m2;
vector<int> vs;
int lazy[MXN<<2];
LL sum[MXN<<2];
void push_down(int rt, int l, int mid, int r) {
    if(lazy[rt] == 0) return;
    lazy[rt<<1] += lazy[rt], lazy[rt<<1|1] += lazy[rt];
    sum[rt<<1] += (LL)lazy[rt] * (vs[mid + 1] - 1 - (vs[l] - 1));
    sum[rt<<1|1] += (LL)lazy[rt] * (vs[r + 1] - 1 - (vs[mid + 1] - 1));
    lazy[rt] = 0;
}
void update(int L, int R, int l, int r, int rt) {
    if(L <= l && r <= R) {
        sum[rt] += vs[R + 1] - 1 - (vs[L] - 1);
//        debug(L, R, vs[R+1] - 1, vs[L] - 1)
        ++ lazy[rt];
        return;
    }
    int mid = (l + r) >> 1;
    push_down(rt, l, mid, r);
    if(L > mid) update(L, R, mid + 1, r, rt<<1|1);
    else if(R <= mid) update(L, R, l, mid, rt<<1);
    else {
        update(L, mid, l, mid, rt<<1), update(mid + 1, R, mid + 1, r, rt<<1|1);
    }
    sum[rt] = sum[rt<<1] + sum[rt<<1|1];
}
int query(LL p, int l, int r, int rt) {
    if(l == r) {
//        debug(l, vs[l], p, sum[rt])
        LL len = sum[rt]/(vs[l+1] - vs[l]);
        return (p + len - 1)/len + vs[l] - 1;
    }
    int mid = (l + r) >> 1;
    push_down(rt, l, mid, r);
//    debug(rt, sum[rt], sum[rt<<1], sum[rt<<1|1])
    if(sum[rt<<1] >= p) return query(p, l, mid, rt<<1);
    else return query(p - sum[rt<<1], mid + 1, r, rt<<1|1);
}
int main() {
#ifndef ONLINE_JUDGE
    freopen("/home/cwolf9/CLionProjects/ccc/in.txt", "r", stdin);
//    freopen("/home/cwolf9/CLionProjects/ccc/out.txt", "w", stdout);
#endif
    n = read();
    xs[1] = read(), xs[2] = read(), a1 = read(), b1 = read(), c1 = read(), m1 = read();
    ys[1] = read(), ys[2] = read(), a2 = read(), b2 = read(), c2 = read(), m2 = read();
    vs.eb(0);
    vs.eb(ls[1] = sml(xs[1], ys[1]) + 1), vs.eb((rs[1] = big(xs[1], ys[1]) + 1)+1);
    vs.eb(ls[2] = sml(xs[2], ys[2]) + 1), vs.eb((rs[2] = big(xs[2], ys[2]) + 1)+1);
    for(int i = 3; i <= n; ++i) {
        xs[i] = (xs[i-1] * a1 + xs[i-2] * b1 + c1)%m1, ys[i] = (ys[i-1] * a2 + ys[i-2] * b2 + c2)%m2;
        vs.eb(ls[i] = sml(xs[i], ys[i]) + 1), vs.eb((rs[i] = big(xs[i], ys[i]) + 1)+1);
    }
    my_unique(vs);
    for(auto x: vs) printf("%d ", x); printf("\n");
    for(int i = 1, tx, ty; i <= n; ++i) {
        tx = lower_bound(all(vs), ls[i]) - vs.begin();
        ty = upper_bound(all(vs), rs[i]) - vs.begin();
//        debug(tx, ty, vs.size())
        update(tx, ty - 1                                           , 1, vs.size(), 1);
//        debug(sum[1], sum[1]/2+(sum[1]%2))
        printf("%d\n", query(sum[1]/2+(sum[1]%2), 1, vs.size(), 1));
//        debug(sum[1])
//        if(i == 2) break;
    }
    return 0;
}